Find max value of x^2 −3xy−2y^2 subject to x^2 +xy+y^2 =1.


Question and Answers Forum

All Questions Topic List
Differentiation Questions
Previous in All Question Next in All Question
Previous in Differentiation Next in Differentiation
Question Number 138851 by bramlexs22 last updated on 19/Apr/21

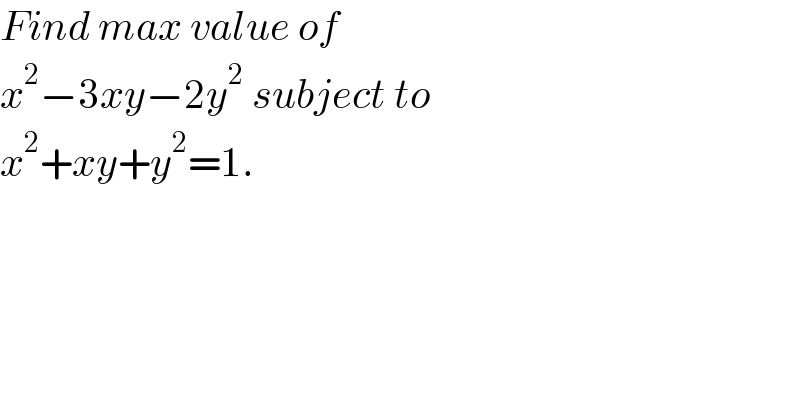
$F i n d m a x v a l u e o f$ $x^{2} - 3 x y - 2 y^{2} s u b j e c t t o$ $x^{2} + x y + y^{2} = 1 .$
	Answered by ajfour last updated on 19/Apr/21
	$F=x^2 −3xy−2y^2 F=x^2 +3x^2 +3y^2 −3−2y^2 F=4x^2 +y^2 −3 y=−(x/2)±(√((x^2 /4)+1−x^2 )) y=−(x/2)±(√(1−((3x^2 )/4))) F=4x^2 −2−x^2 +(x^2 /2)∓x(√(1−((3x^2 )/4))) F=((7x^2 )/2)−2∓x(√(1−((3x^2 )/4))) (dF/dx)=7x∓{(√(1−((3x^2 )/4)))−((3x^2 )/(4(√(1−((3x^2 )/4)))))}=0 ⇒ 49x^2 =1−((3x^2 )/4)+((9x^4 )/(16−12x^2 ))−((3x^2 )/2) ⇒ ((205x^2 )/4)=1+((9x^4 )/(16−12x^2 )) say x^2 =t ⇒ 205x^2 (4−3x^2 )=16−12x^2 +9x^4 ⇒ 624x^4 −832x^2 +16=0 ⇒ 39x^4 −52x^2 +1=0 x^2 =(2/3)±(√((4/9)−(1/(39)))) x^2 =(2/3)±(7/(3(√(13)))) but x^2 <(4/3) now compare F=((7x^2 )/2)−2+(√(x^2 −((3x^4 )/4))) for x^2 =0, (4/3), (2/3)±(7/(3(√(13)))) F(x^2 =0)=−2 F(x^2 =(4/3))=(8/3)≈2.6667 F(x^2 =(2/3)+(7/(3(√(13)))))≈ 2.737 F(x^2 =(2/3)−(7/(3(√(13)))))≈ −1.793 ⇒ F_(max) =F(x^2 =(2/3)+(7/(3(√(13))))) = (7/2)(((26+7(√(13)))/(39)))+{(((26+7(√(13)))/(39)))[1−(3/4)(((26+7(√(13)))/(39)))]}^(1/2) ≈ 2.737$
	$F = x^{2} - 3 x y - 2 y^{2}$ $F = x^{2} + 3 x^{2} + 3 y^{2} - 3 - 2 y^{2}$ $F = 4 x^{2} + y^{2} - 3$ $y = - \frac{x}{2} \pm \sqrt{\frac{x^{2}}{4} + 1 - x^{2}}$ $y = - \frac{x}{2} \pm \sqrt{1 - \frac{3 x^{2}}{4}}$ $F = 4 x^{2} - 2 - x^{2} + \frac{x^{2}}{2} \mp x \sqrt{1 - \frac{3 x^{2}}{4}}$ $F = \frac{7 x^{2}}{2} - 2 \mp x \sqrt{1 - \frac{3 x^{2}}{4}}$ $\frac{d F}{d x} = 7 x \mp {\sqrt{1 - \frac{3 x^{2}}{4}} - \frac{3 x^{2}}{4 \sqrt{1 - \frac{3 x^{2}}{4}}}} = 0$ $\Rightarrow 49 x^{2} = 1 - \frac{3 x^{2}}{4} + \frac{9 x^{4}}{16 - 12 x^{2}} - \frac{3 x^{2}}{2}$ $\Rightarrow \frac{205 x^{2}}{4} = 1 + \frac{9 x^{4}}{16 - 12 x^{2}}$ $s a y x^{2} = t$ $\Rightarrow 205 x^{2} (4 - 3 x^{2}) = 16 - 12 x^{2} + 9 x^{4}$ $\Rightarrow 624 x^{4} - 832 x^{2} + 16 = 0$ $\Rightarrow 39 x^{4} - 52 x^{2} + 1 = 0$ $x^{2} = \frac{2}{3} \pm \sqrt{\frac{4}{9} - \frac{1}{39}}$ $x^{2} = \frac{2}{3} \pm \frac{7}{3 \sqrt{13}}$ $b u t x^{2} < \frac{4}{3}$ $n o w c o m p a r e$ $F = \frac{7 x^{2}}{2} - 2 + \sqrt{x^{2} - \frac{3 x^{4}}{4}}$ $f o r x^{2} = 0, \frac{4}{3}, \frac{2}{3} \pm \frac{7}{3 \sqrt{13}}$ $F (x^{2} = 0) = - 2$ $F (x^{2} = \frac{4}{3}) = \frac{8}{3} \approx 2.6667$ $F (x^{2} = \frac{2}{3} + \frac{7}{3 \sqrt{13}}) \approx 2.737$ $F (x^{2} = \frac{2}{3} - \frac{7}{3 \sqrt{13}}) \approx - 1.793$ $\Rightarrow F_{m a x} = F (x^{2} = \frac{2}{3} + \frac{7}{3 \sqrt{13}})$ $= \frac{7}{2} (\frac{26 + 7 \sqrt{13}}{39}) + {(\frac{26 + 7 \sqrt{13}}{39}) [1 - \frac{3}{4} (\frac{26 + 7 \sqrt{13}}{39})]}^{1 / 2}$ $\approx 2.737$
	Commented by ajfour last updated on 19/Apr/21

	Answered by mr W last updated on 19/Apr/21

	$s a y k = x^{2} - 3 x y - 2 y^{2}$ $F = x^{2} - 3 x y - 2 y^{2} + λ (x^{2} + x y + y^{2} - 1)$ $\frac{\partial F}{\partial x} = 2 x - 3 y + λ (2 x + y) = 0$ $\Rightarrow 2 (1 + λ) x - (3 - λ) y = 0 . . . (i)$ $\frac{\partial F}{\partial y} = - 3 x - 4 y + λ (x + 2 y) = 0$ $\Rightarrow (λ - 3) x + 2 (λ - 2) y = 0 . . . (i i)$ $\frac{x}{y} = \frac{3 - λ}{2 (1 + λ)} = \frac{2 (λ - 2)}{3 - λ}$ $\Rightarrow 3 λ^{2} + 2 λ - 17 = 0$ $λ = \frac{- 1 \pm 2 \sqrt{13}}{3}$ $\Rightarrow \frac{x}{y} = \frac{2 (λ - 2)}{3 - λ} = \frac{\pm \sqrt{13} - 3}{4} = δ$ $x^{2} + x y + y^{2} = 1 \Rightarrow y^{2} = \frac{1}{δ^{2} + δ + 1}$ $k = (δ^{2} - 3 δ - 2) y^{2} = \frac{δ^{2} - 3 δ - 2}{δ^{2} + δ + 1}$ $w i t h δ = \frac{\sqrt{13} - 3}{4} :$ $k_{m i n} = \frac{1 - 2 \sqrt{13}}{3} \approx - 2.070368$ $w i t h δ = \frac{- \sqrt{13} - 3}{4} :$ $k_{m a x} = \frac{1 + 2 \sqrt{13}}{3} \approx 2.737034$
	Commented by mr W last updated on 19/Apr/21

	Commented by mr W last updated on 19/Apr/21

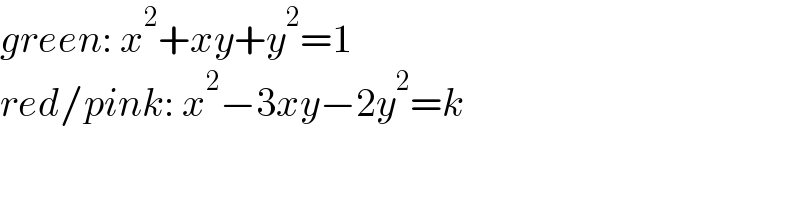
	$g r e e n : x^{2} + x y + y^{2} = 1$ $r e d / p i n k : x^{2} - 3 x y - 2 y^{2} = k$
	Answered by ajfour last updated on 19/Apr/21

	$l e t y = t x$ $x^{2} (1 + t + t^{2}) = 1$ $f (x, t) = f = x^{2} (1 - 3 t - 2 t^{2})$ $f = \frac{1 - 3 t - 2 t^{2}}{t^{2} + t + 1}$ $f = - 2 - \frac{t - 3}{t^{2} + t + 1}$ $f = - 2 - \frac{1}{t + 4 + \frac{13}{t - 3}}$ $f = - 2 - \frac{1}{t - 3 + \frac{13}{t - 3} + 7}$ $f i s f_{m a x} i f h (t) = t - 3 + \frac{13}{t - 3} + 7$ $i s n e g a t i v e w i t h m i n i m u m$ $a b s o l u t e v a l u e .$ $h^{'} (t) = 1 - \frac{13}{{(t - 3)}^{2}} = 0$ $a t t - 3 = - \sqrt{13}$ $h_{m i n} = 7 - 2 \sqrt{13}$ $f_{m a x} = - 2 + \frac{1}{2 \sqrt{13} - 7}$ $= - 2 + \frac{2 \sqrt{13} + 7}{3}$ $f_{m a x} = \frac{2 \sqrt{13} + 1}{3} \approx 2.73703418$
	Commented by ajfour last updated on 19/Apr/21

	Commented by mr W last updated on 20/Apr/21

	$n i c e a p p r o a c h!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum