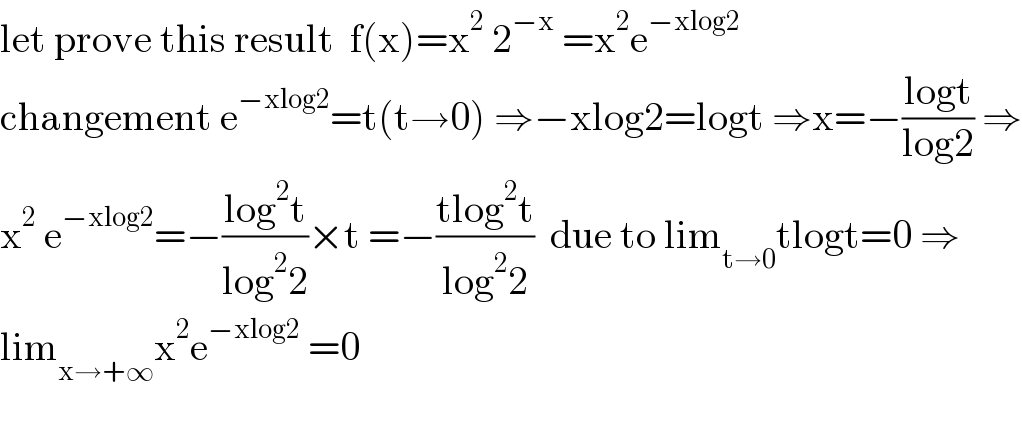Question and Answers Forum
Question Number 138888 by mathdanisur last updated on 19/Apr/21
![Calculus: lim_(x→∞) [ (x^2 /2^x ) + (2^x /(x!)) + ((x!)/x^x ) ] = ?](Q138888.png)
Answered by mathmax by abdo last updated on 20/Apr/21
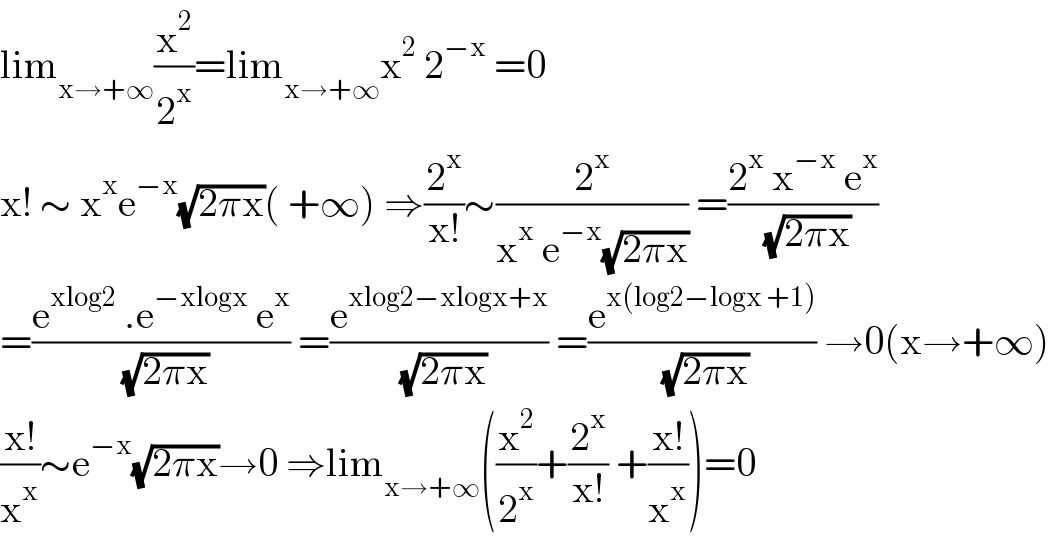
Commented by mathdanisur last updated on 20/Apr/21
Commented by Rasheed.Sindhi last updated on 20/Apr/21

Commented by mnjuly1970 last updated on 20/Apr/21
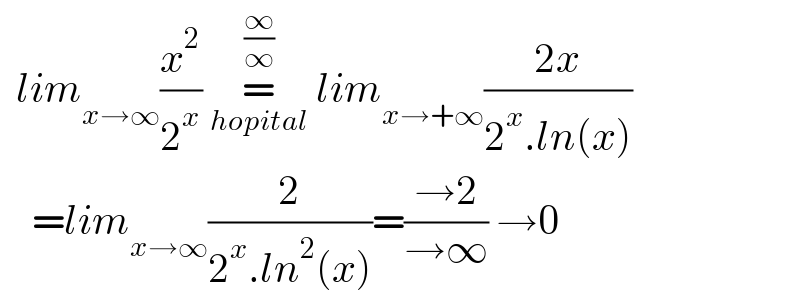
Commented by Rasheed.Sindhi last updated on 20/Apr/21

Commented by Rasheed.Sindhi last updated on 20/Apr/21
Commented by mathmax by abdo last updated on 20/Apr/21
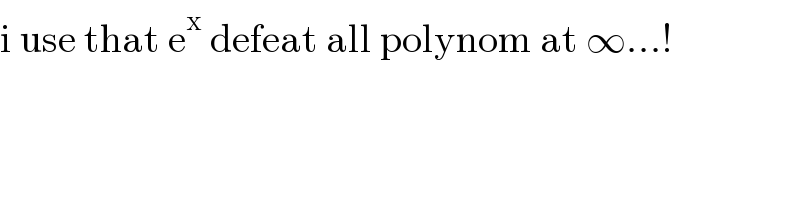
Commented by mathmax by abdo last updated on 20/Apr/21