Question Number 138896 by ajfour last updated on 19/Apr/21
Answered by ajfour last updated on 20/Apr/21
![Let A be origin and x axis vertically down towards center of cube. −dg_x =(((Gdm)x)/((x^2 +y^2 +z^2 )^(3/2) )) −dg_x =(((ρG)xdxdydz)/((x^2 +y^2 +z^2 )^(3/2) )) x∈[0,2a] ; y∈[−a,a] ; z∈[−a,a] −(g_x /(ρG))=∫dz∫dy{(1/( (√(y^2 +z^2 ))))−(1/( (√(4a^2 +y^2 +z^2 ))))} =∫_(−a) ^( a) {ln (((a+(√(a^2 +z^2 )))/(−a+(√(a^2 +z^2 )))))−ln( ((a+(√(5a^2 +z^2 )))/(−a+(√(5a^2 +z^2 )))))}dz ρ=(M/(8a^3 )) & g_0 =−((GM)/R^2 )=−((ρG(8a^3 ))/((((6a^3 )/π))^(2/3) )) as (4/3)πR^3 =8a^3 ⇒ g_0 =−((ρG(8a))/(((6/π))^(2/3) )) ⇒ −ρG=(g_0 /(8a))((6/π))^(2/3) −ρG=((3g_0 )/(4πR)) as a=R((π/6))^(1/3) ⇒ ((g_x (4πR))/(3g_0 ))=∫_(−a) ^( a) {ln (((a+(√(a^2 +z^2 )))/(−a+(√(a^2 +z^2 )))))−ln( ((a+(√(5a^2 +z^2 )))/(−a+(√(5a^2 +z^2 )))))}dz let (z/a)=t ⇒ dz=adt for z=a, t=1 & z=−a, t=−1 so (g_x /g_0 )=((3a)/(4πR))∫_(−1) ^( 1) {ln (((1+(√(1+t^2 )))/(−1+(√(1+t^2 )))))−ln (((1+(√(5+t^2 )))/(−1+(√(5+t^2 )))))}dt (g_x /g_0 )=(1/8)((6/π))^(2/3) ( I_0 )](Q138903.png)
$${Let}\:{A}\:{be}\:{origin}\:{and}\:{x}\:{axis} \\ $$$${vertically}\:{down}\:{towards}\:{center} \\ $$$${of}\:{cube}. \\ $$$$−{dg}_{{x}} =\frac{\left({Gdm}\right){x}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} } \\ $$$$−{dg}_{{x}} =\frac{\left(\rho{G}\right){xdxdydz}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} } \\ $$$${x}\in\left[\mathrm{0},\mathrm{2}{a}\right]\:\:;\:\:{y}\in\left[−{a},{a}\right]\:;\:\:{z}\in\left[−{a},{a}\right] \\ $$$$−\frac{{g}_{{x}} }{\rho{G}}=\int{dz}\int{dy}\left\{\frac{\mathrm{1}}{\:\sqrt{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}{a}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }}\right\} \\ $$$$=\int_{−{a}} ^{\:\:{a}} \left\{\mathrm{ln}\:\left(\frac{{a}+\sqrt{{a}^{\mathrm{2}} +{z}^{\mathrm{2}} }}{−{a}+\sqrt{{a}^{\mathrm{2}} +{z}^{\mathrm{2}} }}\right)−\mathrm{ln}\left(\:\frac{{a}+\sqrt{\mathrm{5}{a}^{\mathrm{2}} +{z}^{\mathrm{2}} }}{−{a}+\sqrt{\mathrm{5}{a}^{\mathrm{2}} +{z}^{\mathrm{2}} }}\right)\right\}{dz} \\ $$$$\rho=\frac{{M}}{\mathrm{8}{a}^{\mathrm{3}} }\:\:\:\&\:\:\:{g}_{\mathrm{0}} =−\frac{{GM}}{{R}^{\mathrm{2}} }=−\frac{\rho{G}\left(\mathrm{8}{a}^{\mathrm{3}} \right)}{\left(\frac{\mathrm{6}{a}^{\mathrm{3}} }{\pi}\right)^{\mathrm{2}/\mathrm{3}} }\: \\ $$$${as}\:\:\:\:\frac{\mathrm{4}}{\mathrm{3}}\pi{R}^{\mathrm{3}} =\mathrm{8}{a}^{\mathrm{3}} \:\:\:\Rightarrow \\ $$$$\:\:\:{g}_{\mathrm{0}} =−\frac{\rho{G}\left(\mathrm{8}{a}\right)}{\left(\frac{\mathrm{6}}{\pi}\right)^{\mathrm{2}/\mathrm{3}} }\:\:\Rightarrow\:−\rho{G}=\frac{{g}_{\mathrm{0}} }{\mathrm{8}{a}}\left(\frac{\mathrm{6}}{\pi}\right)^{\mathrm{2}/\mathrm{3}} \\ $$$$−\rho{G}=\frac{\mathrm{3}{g}_{\mathrm{0}} }{\mathrm{4}\pi{R}}\:\:\:\:{as}\:\:{a}={R}\left(\frac{\pi}{\mathrm{6}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\Rightarrow\:\:\frac{{g}_{{x}} \left(\mathrm{4}\pi{R}\right)}{\mathrm{3}{g}_{\mathrm{0}} }=\int_{−{a}} ^{\:\:{a}} \left\{\mathrm{ln}\:\left(\frac{{a}+\sqrt{{a}^{\mathrm{2}} +{z}^{\mathrm{2}} }}{−{a}+\sqrt{{a}^{\mathrm{2}} +{z}^{\mathrm{2}} }}\right)−\mathrm{ln}\left(\:\frac{{a}+\sqrt{\mathrm{5}{a}^{\mathrm{2}} +{z}^{\mathrm{2}} }}{−{a}+\sqrt{\mathrm{5}{a}^{\mathrm{2}} +{z}^{\mathrm{2}} }}\right)\right\}{dz} \\ $$$${let}\:\:\:\frac{{z}}{{a}}={t}\:\:\Rightarrow\:\:{dz}={adt} \\ $$$${for}\:{z}={a},\:\:{t}=\mathrm{1}\:\:\&\:\:{z}=−{a},\:{t}=−\mathrm{1} \\ $$$${so} \\ $$$$\frac{{g}_{{x}} }{{g}_{\mathrm{0}} }=\frac{\mathrm{3}{a}}{\mathrm{4}\pi{R}}\int_{−\mathrm{1}} ^{\:\mathrm{1}} \left\{\mathrm{ln}\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{−\mathrm{1}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\right)−\mathrm{ln}\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}+{t}^{\mathrm{2}} }}{−\mathrm{1}+\sqrt{\mathrm{5}+{t}^{\mathrm{2}} }}\right)\right\}{dt} \\ $$$$\frac{{g}_{{x}} }{{g}_{\mathrm{0}} }=\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{6}}{\pi}\right)^{\mathrm{2}/\mathrm{3}} \left(\:{I}_{\mathrm{0}} \:\right) \\ $$
Commented by mr W last updated on 20/Apr/21
$${I}_{\mathrm{0}} =\int_{−\mathrm{1}} ^{\:\mathrm{1}} \left\{\mathrm{ln}\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{−\mathrm{1}+\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\right)−\mathrm{ln}\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}+{t}^{\mathrm{2}} }}{−\mathrm{1}+\sqrt{\mathrm{5}+{t}^{\mathrm{2}} }}\right)\right\}{dt} \\ $$$$\:\:\:\:\:\approx\mathrm{5}.\mathrm{193793} \\ $$$${g}_{{x}} =\rho{GI}_{\mathrm{0}} {a} \\ $$$${g}_{\mathrm{0}} =\frac{{GM}}{{R}^{\mathrm{2}} }=\frac{{G}}{{R}^{\mathrm{2}} }×\frac{\rho\mathrm{4}\pi{R}^{\mathrm{3}} }{\mathrm{3}}=\frac{\mathrm{4}\rho{G}\pi{R}}{\mathrm{3}} \\ $$$$\mathrm{8}{a}^{\mathrm{3}} =\frac{\mathrm{4}\pi{R}^{\mathrm{3}} }{\mathrm{3}}\:\Rightarrow\frac{{a}}{{R}}=\left(\frac{\pi}{\mathrm{6}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\frac{{g}_{{x}} }{{g}_{\mathrm{0}} }=\frac{\mathrm{3}{I}_{\mathrm{0}} {a}}{\mathrm{4}\pi{R}}=\frac{{I}_{\mathrm{0}} }{\mathrm{8}}×\frac{\mathrm{6}{a}}{\pi{R}}=\frac{{I}_{\mathrm{0}} }{\mathrm{8}}\left(\frac{\mathrm{6}}{\pi}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \approx\mathrm{0}.\mathrm{999376} \\ $$
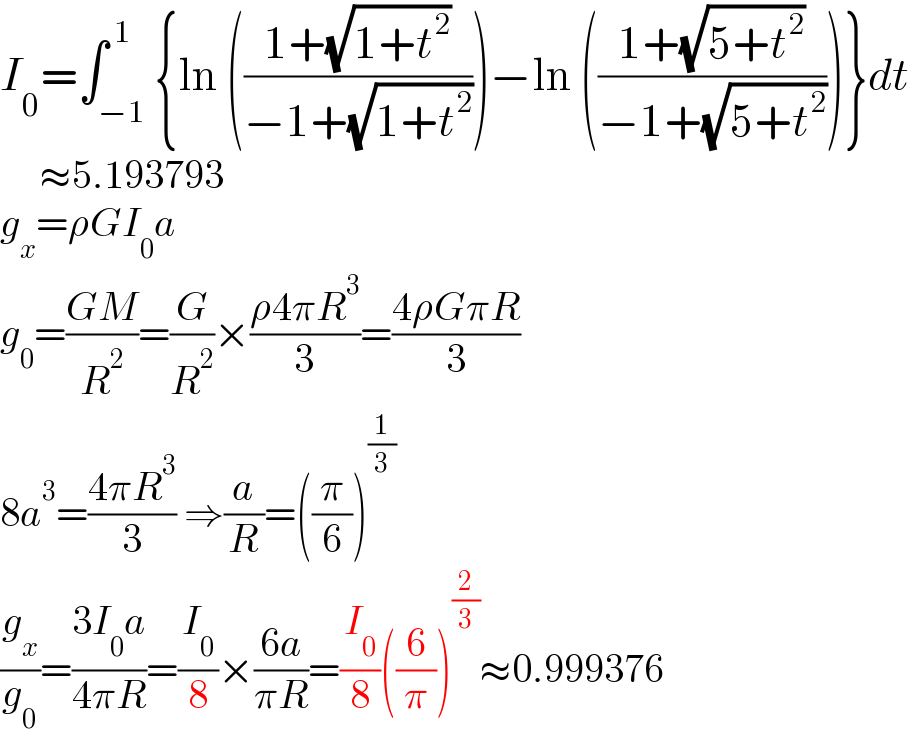
Commented by ajfour last updated on 20/Apr/21
$${If}\:{it}\:{is}\:{correct},\:{it}'{s}\:{rather}\:{strange}.. \\ $$$$\Rightarrow\:{I}_{\mathrm{0}} =\mathrm{8}\left(\frac{{g}_{{cube}} }{{g}_{{sphere}} }\right)_{{A}} \left(\frac{\pi}{\mathrm{6}}\right)^{\mathrm{2}/\mathrm{3}} \\ $$
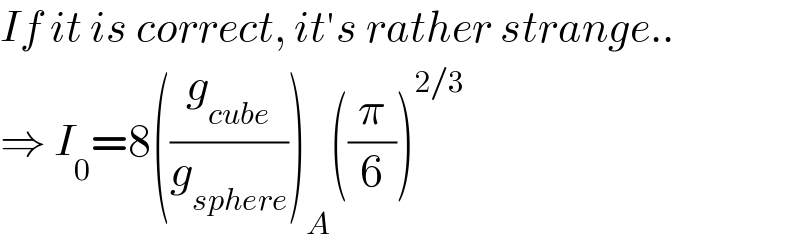
Commented by mr W last updated on 20/Apr/21
$${i}\:{see}\:{this}\:{result}\:{as}\:{understandable}. \\ $$$${the}\:{point}\:{A}\:{is}\:{closer}\:{to}\:{the}\:{center}\:{of} \\ $$$${earth},\:{so}\:{g}_{{x}} \:{should}\:{be}\:{larger}\:{than}\:{g}_{\mathrm{0}} \\ $$$${at}\:{the}\:{surface}\:{of}\:{spherical}\:{earth}.\:{but} \\ $$$${the}\:{mass}\:{of}\:{the}\:{cube}\:{is}\:{less}\: \\ $$$${concentrated}\:{as}\:{the}\:{sphere},\:{so}\:{g}_{{x}} \: \\ $$$${should}\:{be}\:{smaller}\:{than}\:{g}_{\mathrm{0}} .\:{both}\:{effects} \\ $$$${abrogate}\:{each}\:{other},\:{so}\:{g}_{{x}} \:{is}\:{almost} \\ $$$${the}\:{same}\:{as}\:{g}_{\mathrm{0}} \:{at}\:{point}\:{A}. \\ $$
Commented by mr W last updated on 20/Apr/21
Commented by mr W last updated on 20/Apr/21
Commented by mr W last updated on 20/Apr/21
https://possiblywrong.wordpress.com/2011/09/09/if-the-earth-were-a-cube/