
Question and Answers Forum
Question Number 138909 by bramlexs22 last updated on 19/Apr/21
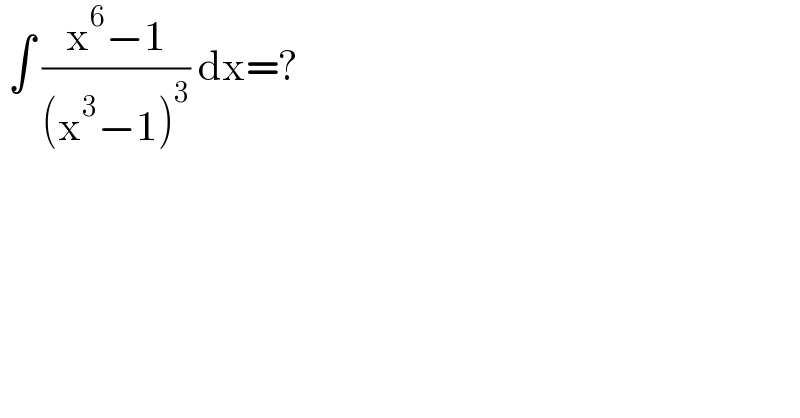
Answered by mathmax by abdo last updated on 20/Apr/21

Answered by phanphuoc last updated on 20/Apr/21

Answered by MJS_new last updated on 20/Apr/21
![∫(((x^3 −1)(x^3 +1))/((x^3 −1)^3 ))dx=∫((x^3 +1)/((x^3 −1)^2 ))dx= [Ostrogradski′s Method] =−((2x)/(3(x^3 −1)))−(1/3)∫(dx/(x^3 −1))= =−((2x)/(3(x^3 −1)))+(1/9)∫((x+2)/(x^2 +x+1))dx−(1/9)∫(dx/(x−1))= =−((2x)/(3(x^3 −1)))+((√3)/9)arctan ((2x+1)/( (√3))) +(1/(18))ln (x^2 +x+1) −(1/9)ln ∣x−1∣ +C](Q138923.png)
| ||
Question and Answers Forum | ||
Question Number 138909 by bramlexs22 last updated on 19/Apr/21 | ||
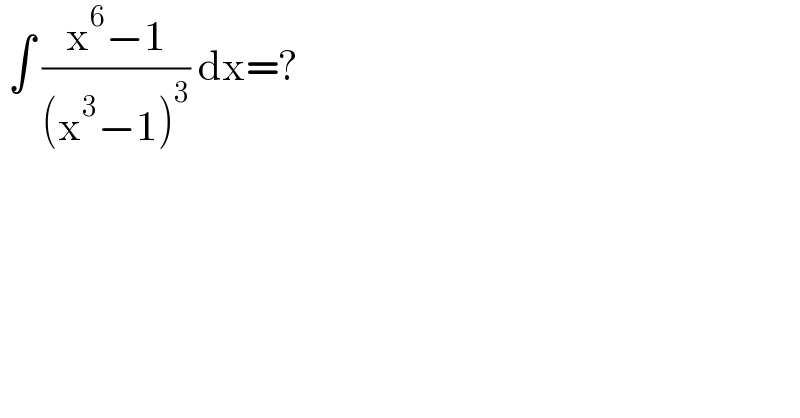 | ||
Answered by mathmax by abdo last updated on 20/Apr/21 | ||
 | ||
| ||
Answered by phanphuoc last updated on 20/Apr/21 | ||
 | ||
| ||
Answered by MJS_new last updated on 20/Apr/21 | ||
![∫(((x^3 −1)(x^3 +1))/((x^3 −1)^3 ))dx=∫((x^3 +1)/((x^3 −1)^2 ))dx= [Ostrogradski′s Method] =−((2x)/(3(x^3 −1)))−(1/3)∫(dx/(x^3 −1))= =−((2x)/(3(x^3 −1)))+(1/9)∫((x+2)/(x^2 +x+1))dx−(1/9)∫(dx/(x−1))= =−((2x)/(3(x^3 −1)))+((√3)/9)arctan ((2x+1)/( (√3))) +(1/(18))ln (x^2 +x+1) −(1/9)ln ∣x−1∣ +C](Q138923.png) | ||
| ||