
Question and Answers Forum
Question Number 138916 by mathsuji last updated on 20/Apr/21
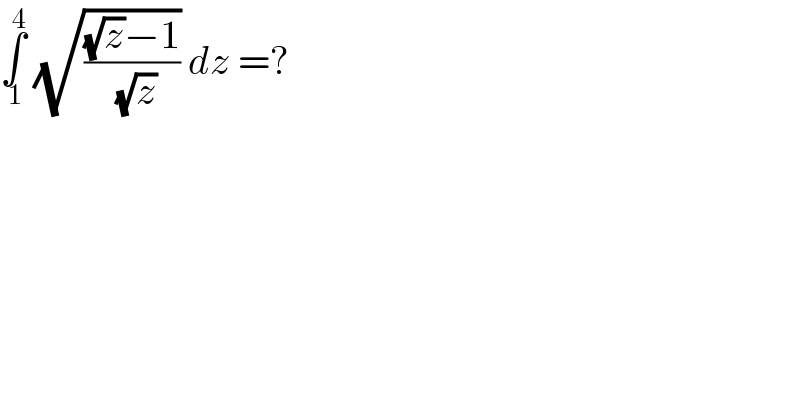
Answered by bramlexs22 last updated on 20/Apr/21
![(√(((√z)−1)/( (√z)))) = r ; (((√z) −1)/( (√z))) = r^2 → { ((z=1→r=0)),((z=4→r=(√(1/2)))) :} ⇒r^2 (√z) = (√z) −1 ⇒(√z) = (1/(1−r^2 )) ; z = (1−r^2 )^(−2) dz = −2(−2r)(1−r^2 )^(−3) dr dz = ((4r)/((1−r^2 )^3 )) dr I= ∫_0 ^((√2)/2) r(((4r)/((1−r^2 )^3 )))dr I=∫ 2r(((2r)/((1−r^2 )^3 )))dr by parts { ((u=2r⇒du=2dr)),((v=−∫ ((d(1−r^2 ))/((1−r^2 )^3 ))=(1/(2(1−r^2 )^2 )))) :} I= [ (r/((1−r^2 )^2 )) ]_0 ^((√2)/2) +∫_( 0) ^( ((√2)/2)) (dr/((1−r^2 )^2 )) now you can solve it](Q138922.png)
Answered by Ankushkumarparcha last updated on 20/Apr/21
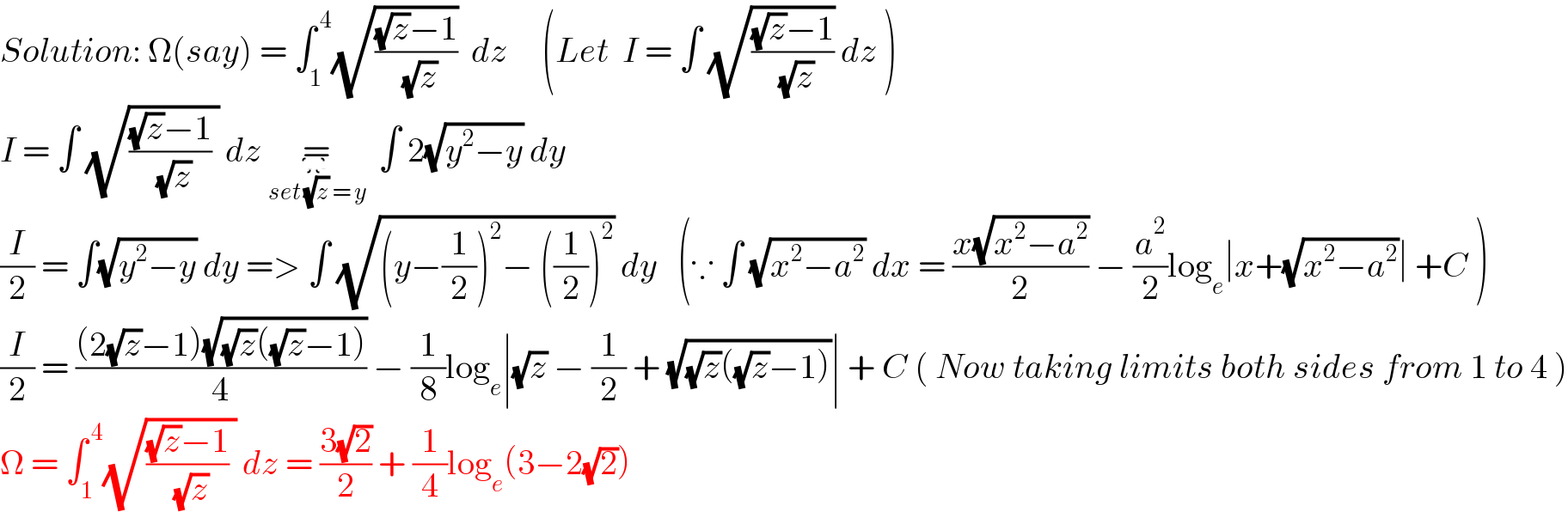
| ||
Question and Answers Forum | ||
Question Number 138916 by mathsuji last updated on 20/Apr/21 | ||
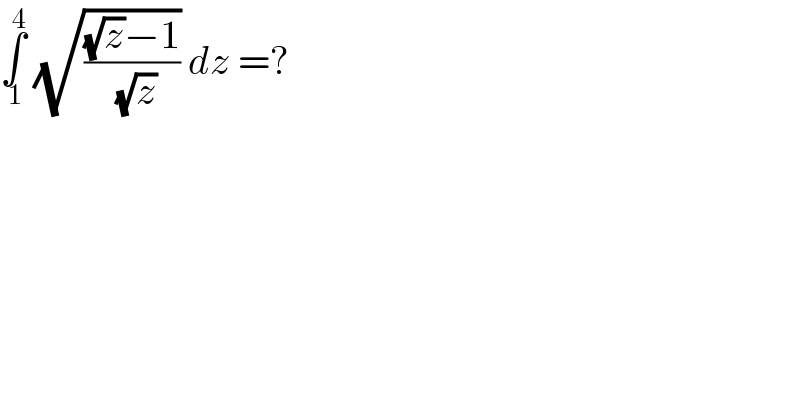 | ||
Answered by bramlexs22 last updated on 20/Apr/21 | ||
![(√(((√z)−1)/( (√z)))) = r ; (((√z) −1)/( (√z))) = r^2 → { ((z=1→r=0)),((z=4→r=(√(1/2)))) :} ⇒r^2 (√z) = (√z) −1 ⇒(√z) = (1/(1−r^2 )) ; z = (1−r^2 )^(−2) dz = −2(−2r)(1−r^2 )^(−3) dr dz = ((4r)/((1−r^2 )^3 )) dr I= ∫_0 ^((√2)/2) r(((4r)/((1−r^2 )^3 )))dr I=∫ 2r(((2r)/((1−r^2 )^3 )))dr by parts { ((u=2r⇒du=2dr)),((v=−∫ ((d(1−r^2 ))/((1−r^2 )^3 ))=(1/(2(1−r^2 )^2 )))) :} I= [ (r/((1−r^2 )^2 )) ]_0 ^((√2)/2) +∫_( 0) ^( ((√2)/2)) (dr/((1−r^2 )^2 )) now you can solve it](Q138922.png) | ||
| ||
Answered by Ankushkumarparcha last updated on 20/Apr/21 | ||
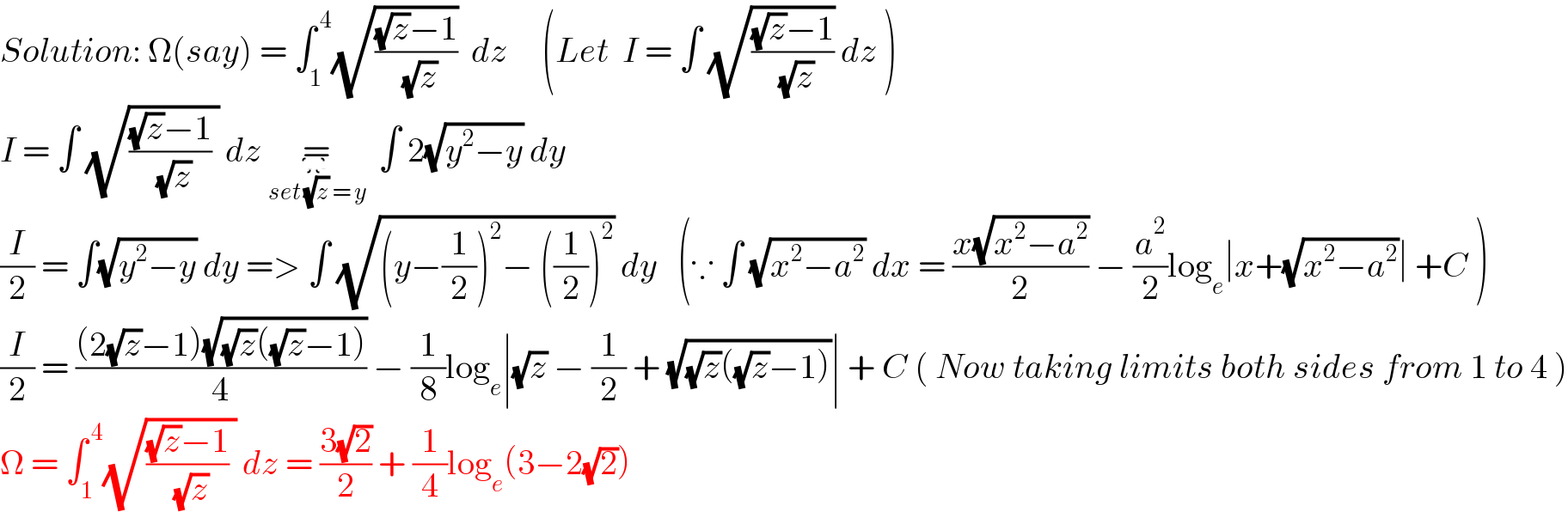 | ||
| ||