
Question and Answers Forum
Question Number 138989 by metamorfose last updated on 20/Apr/21
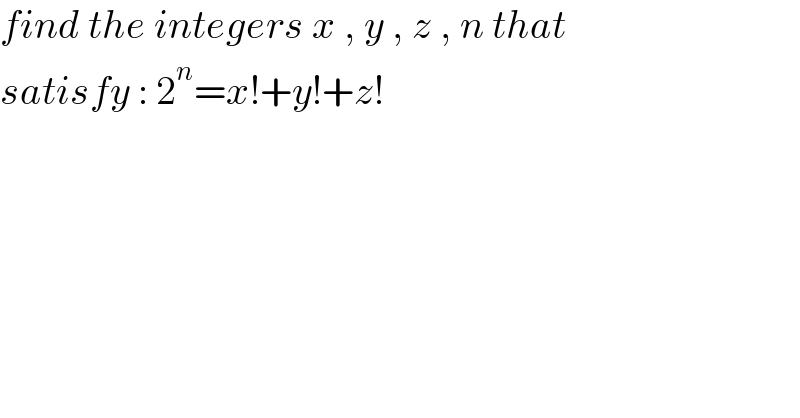
Answered by mindispower last updated on 21/Apr/21
![let m=min(x,y,z),if m≥3⇒ x!+y!+z!≡0[3]⇔2^n ≡0[3] impossib since 2,3 are coprime ⇒m∈{0,1,2} by symetrie of x!+y!+z! let m=x,x≤y≤z x=0,1⇒2^n −1=z!+y!≥2⇒n≥2 z!+y!≡1[2]⇒y={0,1} ⇒2^n −2=z!⇒2(2^(n−1) −1)=z!,we see z≥2 since 2∣2(2^(n−1) −1) the power of 2 in the 2(2^(n−1) −1)is one since 2^(n−1) −1≡1[2]⇒z<4⇒z∈{2,3} z=2⇒2^n −2=2⇒n=2 z=3⇒2^n =8⇒n=3 case 2 x=2 ⇒2^n −2=y!+z!⇒2(2^(n−1) −1)=y!+z!,2≤y<4 because power of 2 in 2(2^(n−1) −1)=1 and y≤z if y≥4⇒4∣(y!+z!) ⇒power of 2 in y!+z! is at less 2 impossibl if y=2 ⇒2^2 (2^(n−2) −1)=z!⇒no solution y=3⇒2(2^(n−1) −1)=6+z! ⇒2^3 (2^(n−3) −1)=z!⇒z={4,5} z=4⇒24=2^n −8⇒n=5 z=5⇒128=2^n ⇒n=7,ander permutation of x,y,z](Q139019.png)
Commented by metamorfose last updated on 21/Apr/21

| ||
Question and Answers Forum | ||
Question Number 138989 by metamorfose last updated on 20/Apr/21 | ||
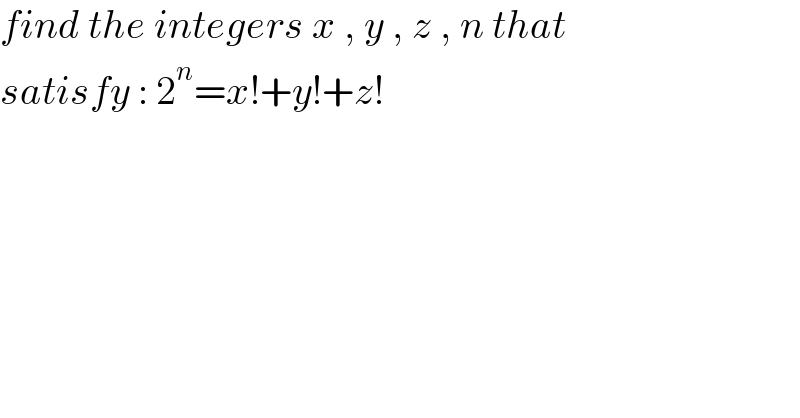 | ||
Answered by mindispower last updated on 21/Apr/21 | ||
![let m=min(x,y,z),if m≥3⇒ x!+y!+z!≡0[3]⇔2^n ≡0[3] impossib since 2,3 are coprime ⇒m∈{0,1,2} by symetrie of x!+y!+z! let m=x,x≤y≤z x=0,1⇒2^n −1=z!+y!≥2⇒n≥2 z!+y!≡1[2]⇒y={0,1} ⇒2^n −2=z!⇒2(2^(n−1) −1)=z!,we see z≥2 since 2∣2(2^(n−1) −1) the power of 2 in the 2(2^(n−1) −1)is one since 2^(n−1) −1≡1[2]⇒z<4⇒z∈{2,3} z=2⇒2^n −2=2⇒n=2 z=3⇒2^n =8⇒n=3 case 2 x=2 ⇒2^n −2=y!+z!⇒2(2^(n−1) −1)=y!+z!,2≤y<4 because power of 2 in 2(2^(n−1) −1)=1 and y≤z if y≥4⇒4∣(y!+z!) ⇒power of 2 in y!+z! is at less 2 impossibl if y=2 ⇒2^2 (2^(n−2) −1)=z!⇒no solution y=3⇒2(2^(n−1) −1)=6+z! ⇒2^3 (2^(n−3) −1)=z!⇒z={4,5} z=4⇒24=2^n −8⇒n=5 z=5⇒128=2^n ⇒n=7,ander permutation of x,y,z](Q139019.png) | ||
| ||
Commented by metamorfose last updated on 21/Apr/21 | ||
 | ||