Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 13903 by tawa tawa last updated on 24/May/17

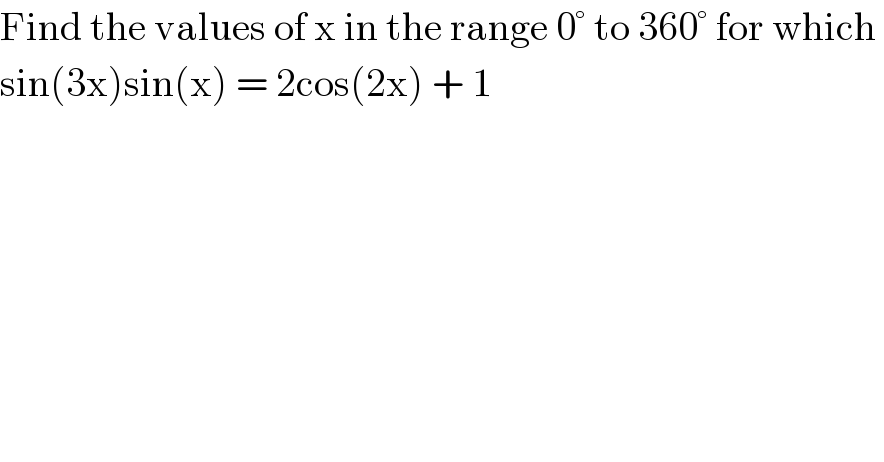
Find the values of x in the range 0° to 360° for which sin(3x)sin(x) = 2cos(2x) + 1

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{x}\:\mathrm{in}\:\mathrm{the}\:\mathrm{range}\:\mathrm{0}°\:\mathrm{to}\:\mathrm{360}°\:\mathrm{for}\:\mathrm{which}\: \\ $$$$\mathrm{sin}\left(\mathrm{3x}\right)\mathrm{sin}\left(\mathrm{x}\right)\:=\:\mathrm{2cos}\left(\mathrm{2x}\right)\:+\:\mathrm{1} \\ $$

Commented by myintkhaing last updated on 26/May/17

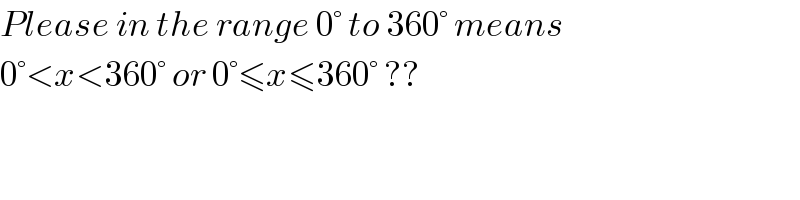
Please in the range 0° to 360° means 0°<x<360° or 0°≤x≤360° ??

$${Please}\:{in}\:{the}\:{range}\:\mathrm{0}°\:{to}\:\mathrm{360}°\:{means} \\ $$$$\mathrm{0}°<{x}<\mathrm{360}°\:{or}\:\mathrm{0}°\leqslant{x}\leqslant\mathrm{360}°\:?? \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/May/17

(3sinx−4sin^3 x)sinx=2(1−2sin^2 x)+1 sinx=t⇒3t^2 −4t^4 =−4t^2 +3⇒ 4t^4 −7t^2 +3=0⇒t^2 =1,(3/4)⇒t=sinx=±1,±((√3)/2) sinx=1⇒x=2kπ+(π/2) sinx=−1⇒x=2kπ+((3π)/2) sinx=((√3)/2)⇒x=2kπ+(π/3),2kπ+((2π)/3) sinx=−((√3)/2)⇒x=2kπ+((4π)/3),2kπ+((5π)/3) ⇒x=(π/3),(π/2),((2π)/3),((4π)/3),((3π)/2),((5π)/3)∈(0,2π) .■

$$\left(\mathrm{3}{sinx}−\mathrm{4}{sin}^{\mathrm{3}} {x}\right){sinx}=\mathrm{2}\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {x}\right)+\mathrm{1} \\ $$$${sinx}={t}\Rightarrow\mathrm{3}{t}^{\mathrm{2}} −\mathrm{4}{t}^{\mathrm{4}} =−\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}\Rightarrow \\ $$$$\mathrm{4}{t}^{\mathrm{4}} −\mathrm{7}{t}^{\mathrm{2}} +\mathrm{3}=\mathrm{0}\Rightarrow{t}^{\mathrm{2}} =\mathrm{1},\frac{\mathrm{3}}{\mathrm{4}}\Rightarrow{t}={sinx}=\pm\mathrm{1},\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${sinx}=\mathrm{1}\Rightarrow{x}=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{2}} \\ $$$${sinx}=−\mathrm{1}\Rightarrow{x}=\mathrm{2}{k}\pi+\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$${sinx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\Rightarrow{x}=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{3}},\mathrm{2}{k}\pi+\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$${sinx}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\Rightarrow{x}=\mathrm{2}{k}\pi+\frac{\mathrm{4}\pi}{\mathrm{3}},\mathrm{2}{k}\pi+\frac{\mathrm{5}\pi}{\mathrm{3}} \\ $$$$\Rightarrow{x}=\frac{\pi}{\mathrm{3}},\frac{\pi}{\mathrm{2}},\frac{\mathrm{2}\pi}{\mathrm{3}},\frac{\mathrm{4}\pi}{\mathrm{3}},\frac{\mathrm{3}\pi}{\mathrm{2}},\frac{\mathrm{5}\pi}{\mathrm{3}}\in\left(\mathrm{0},\mathrm{2}\pi\right)\:\:\:\:.\blacksquare \\ $$

Commented by tawa tawa last updated on 25/May/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by ajfour last updated on 25/May/17

i think x=((2π)/3), ((5π)/3) also qualify in the given range .

$${i}\:{think}\:\:\:{x}=\frac{\mathrm{2}\pi}{\mathrm{3}},\:\frac{\mathrm{5}\pi}{\mathrm{3}}\:{also}\:{qualify}\: \\ $$$${in}\:{the}\:{given}\:{range}\:. \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 25/May/17

you are right sir.thanks.

$${you}\:{are}\:{right}\:{sir}.{thanks}. \\ $$

Answered by ajfour last updated on 25/May/17

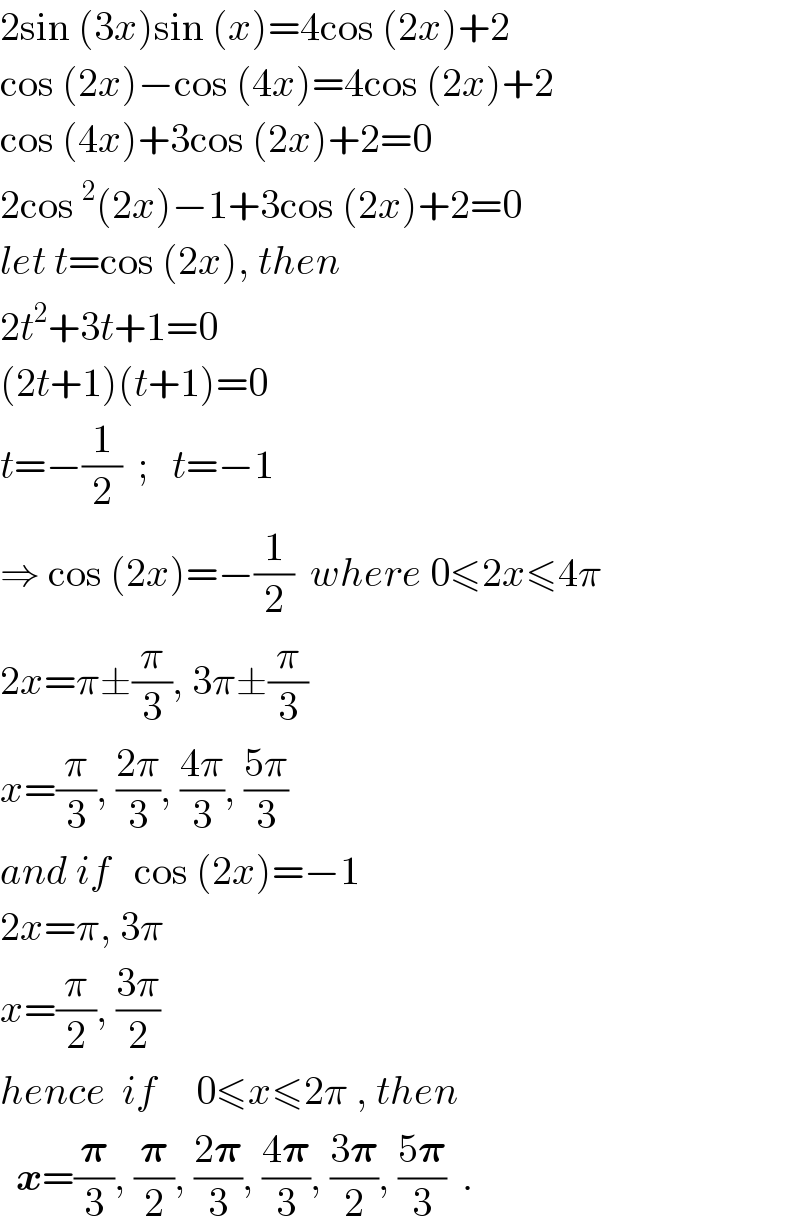
2sin (3x)sin (x)=4cos (2x)+2 cos (2x)−cos (4x)=4cos (2x)+2 cos (4x)+3cos (2x)+2=0 2cos^2 (2x)−1+3cos (2x)+2=0 let t=cos (2x), then 2t^2 +3t+1=0 (2t+1)(t+1)=0 t=−(1/2) ; t=−1 ⇒ cos (2x)=−(1/2) where 0≤2x≤4π 2x=π±(π/3), 3π±(π/3) x=(π/3), ((2π)/3), ((4π)/3), ((5π)/3) and if cos (2x)=−1 2x=π, 3π x=(π/2), ((3π)/2) hence if 0≤x≤2π , then x=(𝛑/3), (𝛑/2), ((2𝛑)/3), ((4𝛑)/3), ((3𝛑)/2), ((5𝛑)/3) .

$$\mathrm{2sin}\:\left(\mathrm{3}{x}\right)\mathrm{sin}\:\left({x}\right)=\mathrm{4cos}\:\left(\mathrm{2}{x}\right)+\mathrm{2} \\ $$$$\mathrm{cos}\:\left(\mathrm{2}{x}\right)−\mathrm{cos}\:\left(\mathrm{4}{x}\right)=\mathrm{4cos}\:\left(\mathrm{2}{x}\right)+\mathrm{2} \\ $$$$\mathrm{cos}\:\left(\mathrm{4}{x}\right)+\mathrm{3cos}\:\left(\mathrm{2}{x}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{2cos}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)−\mathrm{1}+\mathrm{3cos}\:\left(\mathrm{2}{x}\right)+\mathrm{2}=\mathrm{0} \\ $$$${let}\:{t}=\mathrm{cos}\:\left(\mathrm{2}{x}\right),\:{then} \\ $$$$\mathrm{2}{t}^{\mathrm{2}} +\mathrm{3}{t}+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}{t}+\mathrm{1}\right)\left({t}+\mathrm{1}\right)=\mathrm{0} \\ $$$${t}=−\frac{\mathrm{1}}{\mathrm{2}}\:\:;\:\:\:{t}=−\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{cos}\:\left(\mathrm{2}{x}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\:\:{where}\:\mathrm{0}\leqslant\mathrm{2}{x}\leqslant\mathrm{4}\pi \\ $$$$\mathrm{2}{x}=\pi\pm\frac{\pi}{\mathrm{3}},\:\mathrm{3}\pi\pm\frac{\pi}{\mathrm{3}} \\ $$$${x}=\frac{\pi}{\mathrm{3}},\:\frac{\mathrm{2}\pi}{\mathrm{3}},\:\frac{\mathrm{4}\pi}{\mathrm{3}},\:\frac{\mathrm{5}\pi}{\mathrm{3}} \\ $$$${and}\:{if}\:\:\:\mathrm{cos}\:\left(\mathrm{2}{x}\right)=−\mathrm{1} \\ $$$$\mathrm{2}{x}=\pi,\:\mathrm{3}\pi \\ $$$${x}=\frac{\pi}{\mathrm{2}},\:\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$${hence}\:\:{if}\:\:\:\:\:\mathrm{0}\leqslant{x}\leqslant\mathrm{2}\pi\:,\:{then} \\ $$$$\:\:\boldsymbol{{x}}=\frac{\boldsymbol{\pi}}{\mathrm{3}},\:\frac{\boldsymbol{\pi}}{\mathrm{2}},\:\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{3}},\:\frac{\mathrm{4}\boldsymbol{\pi}}{\mathrm{3}},\:\frac{\mathrm{3}\boldsymbol{\pi}}{\mathrm{2}},\:\frac{\mathrm{5}\boldsymbol{\pi}}{\mathrm{3}}\:\:. \\ $$

Commented by mrW1 last updated on 25/May/17

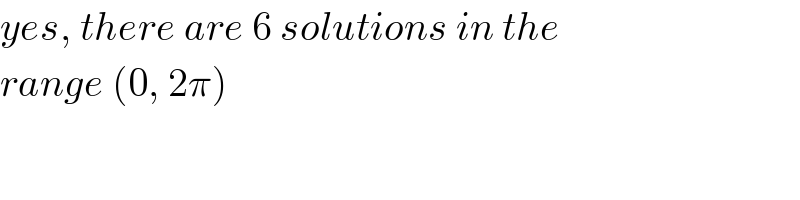
yes, there are 6 solutions in the range (0, 2π)

$${yes},\:{there}\:{are}\:\mathrm{6}\:{solutions}\:{in}\:{the} \\ $$$${range}\:\left(\mathrm{0},\:\mathrm{2}\pi\right) \\ $$

Commented by ajfour last updated on 25/May/17

thanks.

$${thanks}.\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com