
Question and Answers Forum
Question Number 139052 by EnterUsername last updated on 21/Apr/21
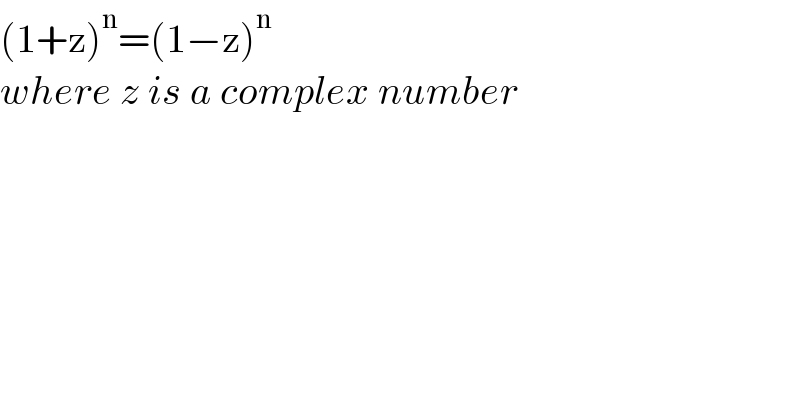
Answered by mathmax by abdo last updated on 21/Apr/21
![z=−1 is not solution let z≠−1 e⇒(((1−z)/(1+z)))^n =1 =e^(i(2kπ)) ⇒((1−z)/(1+z))=e^(i(((2kπ)/n))) k∈[[0,n−1]] ⇒1−z=e^((2ikπ)/n) +e^((2ikπ)/n) z ⇒1−e^((2ikπ)/n) =(1+e^((2ikπ)/n) )z ⇒ z_k =((1−e^((2ikπ)/n) )/(1+e^((2ikπ)/n) )) =((1−cos(((2kπ)/n))−isin(((2kπ)/n)))/(1+cos(((2kπ)/n))+isin(((2kπ)/n)))) =((2sin^2 (((kπ)/n))−2isin(((kπ)/n))cos(((kπ)/n)))/(2cos^2 (((kπ)/n))+2isin(((kπ)/n))cos(((kπ)/n)))) =((−isin(((kπ)/n))e^((ikπ)/n) )/(cos(((kπ)/n))e^((ikπ)/n) )) =−itan(((kπ)/n)) so the solution of this equation are z_k =−itan(((kπ)/n)) k∈[0,n−1]]](Q139064.png)
| ||
Question and Answers Forum | ||
Question Number 139052 by EnterUsername last updated on 21/Apr/21 | ||
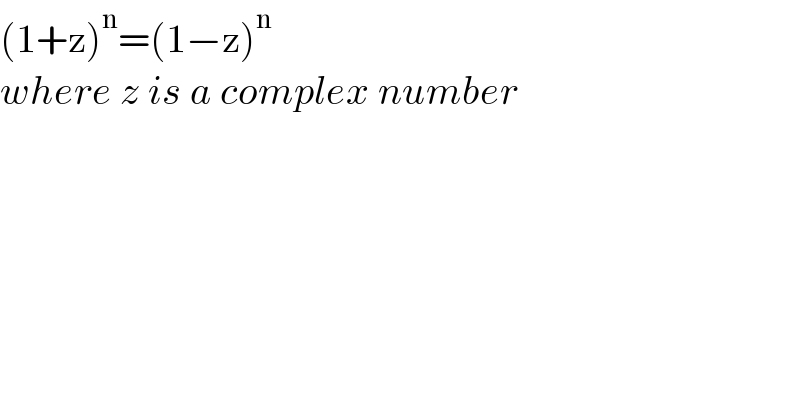 | ||
Answered by mathmax by abdo last updated on 21/Apr/21 | ||
![z=−1 is not solution let z≠−1 e⇒(((1−z)/(1+z)))^n =1 =e^(i(2kπ)) ⇒((1−z)/(1+z))=e^(i(((2kπ)/n))) k∈[[0,n−1]] ⇒1−z=e^((2ikπ)/n) +e^((2ikπ)/n) z ⇒1−e^((2ikπ)/n) =(1+e^((2ikπ)/n) )z ⇒ z_k =((1−e^((2ikπ)/n) )/(1+e^((2ikπ)/n) )) =((1−cos(((2kπ)/n))−isin(((2kπ)/n)))/(1+cos(((2kπ)/n))+isin(((2kπ)/n)))) =((2sin^2 (((kπ)/n))−2isin(((kπ)/n))cos(((kπ)/n)))/(2cos^2 (((kπ)/n))+2isin(((kπ)/n))cos(((kπ)/n)))) =((−isin(((kπ)/n))e^((ikπ)/n) )/(cos(((kπ)/n))e^((ikπ)/n) )) =−itan(((kπ)/n)) so the solution of this equation are z_k =−itan(((kπ)/n)) k∈[0,n−1]]](Q139064.png) | ||
| ||