
Question and Answers Forum
Question Number 139254 by mathdanisur last updated on 25/Apr/21
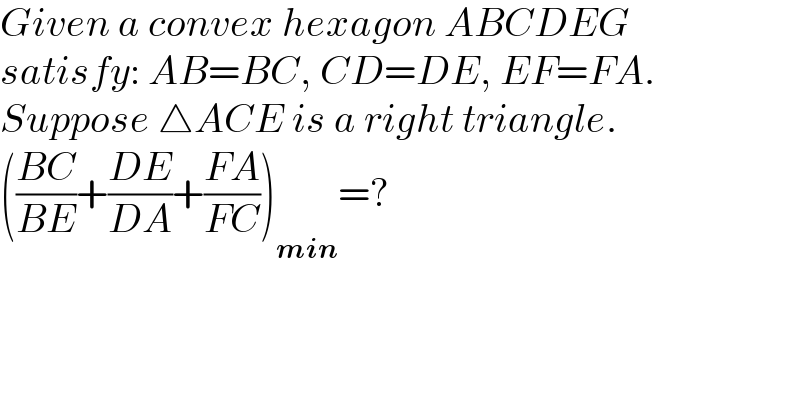
Answered by mr W last updated on 27/Apr/21

Commented by mr W last updated on 27/Apr/21
![BC=(√(a^2 +p^2 )) BE=(√(a^2 +(2b+p)^2 )) P=((BE)/(BC))=((√(a^2 +(2b+p)^2 ))/( (√(a^2 +p^2 ))))=((√(1+(((2b)/a)+(p/a))^2 ))/( (√(1+((p/a))^2 )))) let x=(p/a), λ=(b/a) P=((√(1+(2λ+x)^2 ))/( (√(1+x^2 )))) (dP/dx)=((2(2λ+x))/(2(√(1+(2λ+x)^2 ))(√(1+x^2 ))))−((2x(√(1+(2λ+x)^2 )))/(2(1+x^2 )(√(1+x^2 ))))=0 (((2λ+x))/( (√(1+(2λ+x)^2 ))))=((x(√(1+(2λ+x)^2 )))/((1+x^2 ))) (1+x^2 )(2λ+x)=x[1+(2λ+x)^2 ] x^2 +2λx−1=0 x=(√(λ^2 +1))−λ=1 for λ=(b/a)=1 P_(max) =((√(1+(2+1)^2 ))/( (√(1+1))))=(√5) (((BC)/(BE)))_(min) =(1/P_(max) )=(1/( (√5))) similarly (((DE)/(DA)))_(min) =(1/( (√5))) with b=a, c=(√2)a FA=(√(c^2 +r^2 )) FC=c+r S=((FA)/(FC))=((√(c^2 +r^2 ))/(c+r))=((√(1+((r/c))^2 ))/(1+(r/c))) y=(r/c) S=((√(1+y^2 ))/(1+y)) (dS/dy)=((2y)/(2(√(1+y^2 ))(1+y)))−((√(1+y^2 ))/((1+y)^2 ))=0 (y/( (√(1+y^2 ))))=((√(1+y^2 ))/(1+y)) y^2 +y=1+y^2 y=1 S_(min) =((√(1+1^2 ))/(1+1))=(1/( (√2))) (((BC)/(BE))+((DE)/(DA))+((FA)/(FC)))_(min) =(1/( (√5)))+(1/( (√5)))+(1/( (√2)))=((2(√2)+(√5))/( (√(10))))](Q139475.png)
Commented by mathdanisur last updated on 30/Apr/21

| ||
Question and Answers Forum | ||
Question Number 139254 by mathdanisur last updated on 25/Apr/21 | ||
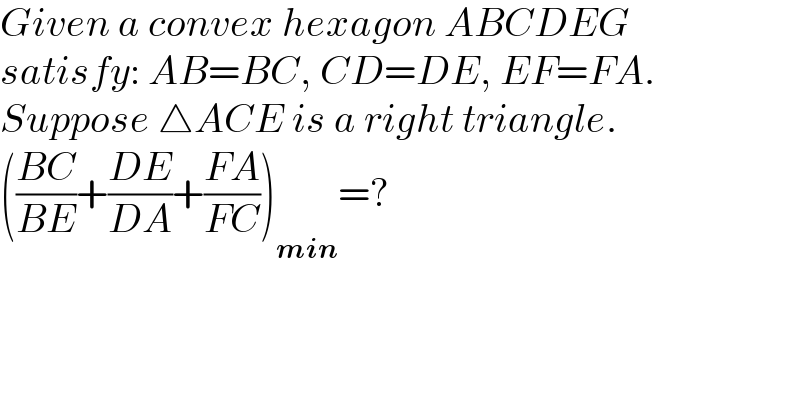 | ||
Answered by mr W last updated on 27/Apr/21 | ||
 | ||
Commented by mr W last updated on 27/Apr/21 | ||
![BC=(√(a^2 +p^2 )) BE=(√(a^2 +(2b+p)^2 )) P=((BE)/(BC))=((√(a^2 +(2b+p)^2 ))/( (√(a^2 +p^2 ))))=((√(1+(((2b)/a)+(p/a))^2 ))/( (√(1+((p/a))^2 )))) let x=(p/a), λ=(b/a) P=((√(1+(2λ+x)^2 ))/( (√(1+x^2 )))) (dP/dx)=((2(2λ+x))/(2(√(1+(2λ+x)^2 ))(√(1+x^2 ))))−((2x(√(1+(2λ+x)^2 )))/(2(1+x^2 )(√(1+x^2 ))))=0 (((2λ+x))/( (√(1+(2λ+x)^2 ))))=((x(√(1+(2λ+x)^2 )))/((1+x^2 ))) (1+x^2 )(2λ+x)=x[1+(2λ+x)^2 ] x^2 +2λx−1=0 x=(√(λ^2 +1))−λ=1 for λ=(b/a)=1 P_(max) =((√(1+(2+1)^2 ))/( (√(1+1))))=(√5) (((BC)/(BE)))_(min) =(1/P_(max) )=(1/( (√5))) similarly (((DE)/(DA)))_(min) =(1/( (√5))) with b=a, c=(√2)a FA=(√(c^2 +r^2 )) FC=c+r S=((FA)/(FC))=((√(c^2 +r^2 ))/(c+r))=((√(1+((r/c))^2 ))/(1+(r/c))) y=(r/c) S=((√(1+y^2 ))/(1+y)) (dS/dy)=((2y)/(2(√(1+y^2 ))(1+y)))−((√(1+y^2 ))/((1+y)^2 ))=0 (y/( (√(1+y^2 ))))=((√(1+y^2 ))/(1+y)) y^2 +y=1+y^2 y=1 S_(min) =((√(1+1^2 ))/(1+1))=(1/( (√2))) (((BC)/(BE))+((DE)/(DA))+((FA)/(FC)))_(min) =(1/( (√5)))+(1/( (√5)))+(1/( (√2)))=((2(√2)+(√5))/( (√(10))))](Q139475.png) | ||
Commented by mathdanisur last updated on 30/Apr/21 | ||
 | ||