Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 139342 by BHOOPENDRA last updated on 26/Apr/21

Commented by BHOOPENDRA last updated on 26/Apr/21

mr.W sir help me out this

$${mr}.{W}\:{sir}\:{help}\:{me}\:{out}\:{this} \\ $$

Answered by mr W last updated on 26/Apr/21

Commented by mr W last updated on 26/Apr/21

if n masses are in balance about the rotation point (origin), then Σ_(k=1) ^n m_k x_k =Σ_(k=1) ^n m_k r_k cos θ_k =0 Σ_(k=1) ^n m_k y_k =Σ_(k=1) ^n m_k r_k sin θ_k =0 in our case m_5 , θ_5 are unknown. Σ_(k=1) ^4 m_k r_k cos θ_k +m_5 r_5 cos θ_5 =0 ⇒m_5 cos θ_5 =−((Σ_(k=1) ^4 m_k r_k cos θ_k )/r_5 ) ...(i) Σ_(k=1) ^4 m_k r_k sin θ_k +m_5 r_5 sin θ_5 =0 ⇒m_5 sin θ_5 =−((Σ_(k=1) ^4 m_k r_k sin θ_k )/r_5 ) ...(ii) (i)^2 +(ii)^2 : m_5 =((√((Σ_(k=1) ^4 m_k r_k cos θ_k )^2 +(Σ_(k=1) ^4 m_k r_k sin θ_k )^2 ))/r_5 ^2 ) (ii)/(i): tan θ_5 =((Σ_(k=1) ^4 m_k r_k sin θ_k )/(Σ_(k=1) ^4 m_k r_k cos θ_k )) θ_5 =tan^(−1) (((Σ_(k=1) ^4 m_k r_k sin θ_k )/(Σ_(k=1) ^4 m_k r_k cos θ_k ))) ( +π ) determinant ((k,m_k ,r_k ,θ_k ),(1,(220),(0.22),(0°)),(2,(330),(0.18),(40°)),(3,(220),(0.24),(120°)),(4,(240),(0.32),(265°)),(5,?,(0.20),?)) Σ_(k=1) ^4 m_k r_k cos θ_k =60.809479 Σ_(k=1) ^4 m_k r_k sin θ_k =7.399973 ⇒m_5 =((√((60.809479)^2 +(7.399973)^2 ))/(0.20^2 ))=1531.452kg tan θ_5 =((7.399973)/(60.809473)) ⇒θ_5 =6.983°

$${if}\:{n}\:{masses}\:{are}\:{in}\:{balance}\:{about}\:{the} \\ $$$${rotation}\:{point}\:\left({origin}\right),\:{then} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{m}_{{k}} {x}_{{k}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{cos}\:\theta_{{k}} =\mathrm{0} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{m}_{{k}} {y}_{{k}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{sin}\:\theta_{{k}} =\mathrm{0} \\ $$$${in}\:{our}\:{case}\:{m}_{\mathrm{5}} ,\:\theta_{\mathrm{5}} \:{are}\:{unknown}. \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{cos}\:\theta_{{k}} +{m}_{\mathrm{5}} {r}_{\mathrm{5}} \mathrm{cos}\:\theta_{\mathrm{5}} =\mathrm{0} \\ $$$$\Rightarrow{m}_{\mathrm{5}} \mathrm{cos}\:\theta_{\mathrm{5}} =−\frac{\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{cos}\:\theta_{{k}} }{{r}_{\mathrm{5}} }\:\:\:\:...\left({i}\right) \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{sin}\:\theta_{{k}} +{m}_{\mathrm{5}} {r}_{\mathrm{5}} \mathrm{sin}\:\theta_{\mathrm{5}} =\mathrm{0} \\ $$$$\Rightarrow{m}_{\mathrm{5}} \mathrm{sin}\:\theta_{\mathrm{5}} =−\frac{\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{sin}\:\theta_{{k}} }{{r}_{\mathrm{5}} }\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)^{\mathrm{2}} +\left({ii}\right)^{\mathrm{2}} : \\ $$$${m}_{\mathrm{5}} =\frac{\sqrt{\left(\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{cos}\:\theta_{{k}} \right)^{\mathrm{2}} +\left(\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{sin}\:\theta_{{k}} \right)^{\mathrm{2}} }}{{r}_{\mathrm{5}} ^{\mathrm{2}} } \\ $$$$\left({ii}\right)/\left({i}\right): \\ $$$$\mathrm{tan}\:\theta_{\mathrm{5}} =\frac{\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{sin}\:\theta_{{k}} }{\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{cos}\:\theta_{{k}} } \\ $$$$\theta_{\mathrm{5}} =\mathrm{tan}^{−\mathrm{1}} \left(\frac{\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{sin}\:\theta_{{k}} }{\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{cos}\:\theta_{{k}} }\right)\:\:\:\left(\:+\pi\:\right) \\ $$$$\begin{array}{|c|c|c|c|c|c|}{{k}}&\hline{{m}_{{k}} }&\hline{{r}_{{k}} }&\hline{\theta_{{k}} }\\{\mathrm{1}}&\hline{\mathrm{220}}&\hline{\mathrm{0}.\mathrm{22}}&\hline{\mathrm{0}°}\\{\mathrm{2}}&\hline{\mathrm{330}}&\hline{\mathrm{0}.\mathrm{18}}&\hline{\mathrm{40}°}\\{\mathrm{3}}&\hline{\mathrm{220}}&\hline{\mathrm{0}.\mathrm{24}}&\hline{\mathrm{120}°}\\{\mathrm{4}}&\hline{\mathrm{240}}&\hline{\mathrm{0}.\mathrm{32}}&\hline{\mathrm{265}°}\\{\mathrm{5}}&\hline{?}&\hline{\mathrm{0}.\mathrm{20}}&\hline{?}\\\hline\end{array} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{cos}\:\theta_{{k}} =\mathrm{60}.\mathrm{809479} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}{m}_{{k}} {r}_{{k}} \mathrm{sin}\:\theta_{{k}} =\mathrm{7}.\mathrm{399973} \\ $$$$\Rightarrow{m}_{\mathrm{5}} =\frac{\sqrt{\left(\mathrm{60}.\mathrm{809479}\right)^{\mathrm{2}} +\left(\mathrm{7}.\mathrm{399973}\right)^{\mathrm{2}} }}{\mathrm{0}.\mathrm{20}^{\mathrm{2}} }=\mathrm{1531}.\mathrm{452}{kg} \\ $$$$\mathrm{tan}\:\theta_{\mathrm{5}} =\frac{\mathrm{7}.\mathrm{399973}}{\mathrm{60}.\mathrm{809473}} \\ $$$$\Rightarrow\theta_{\mathrm{5}} =\mathrm{6}.\mathrm{983}° \\ $$

Commented by BHOOPENDRA last updated on 26/Apr/21

thankyou

$${thankyou}\: \\ $$

Answered by TheSupreme last updated on 26/Apr/21

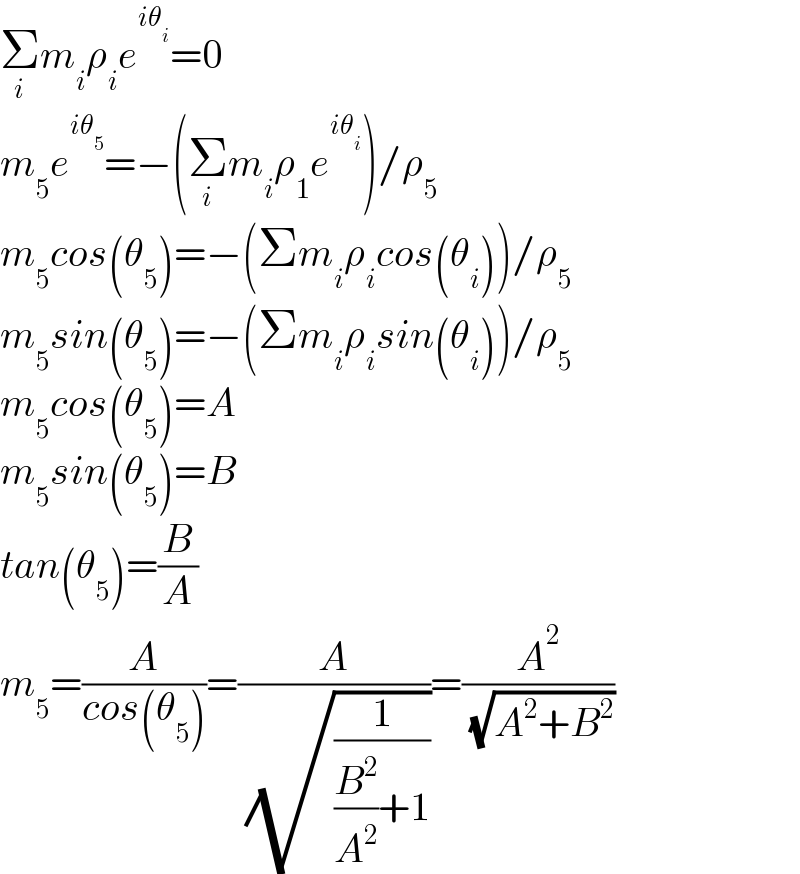
Σ_i m_i ρ_i e^(iθ_i ) =0 m_5 e^(iθ_5 ) =−(Σ_i m_i ρ_1 e^(iθ_i ) )/ρ_5 m_5 cos(θ_5 )=−(Σm_i ρ_i cos(θ_i ))/ρ_5 m_5 sin(θ_5 )=−(Σm_i ρ_i sin(θ_i ))/ρ_5 m_5 cos(θ_5 )=A m_5 sin(θ_5 )=B tan(θ_5 )=(B/A) m_5 =(A/(cos(θ_5 )))=(A/( (√(1/((B^2 /A^2 )+1)))))=(A^2 /( (√(A^2 +B^2 ))))

$$\underset{{i}} {\sum}{m}_{{i}} \rho_{{i}} {e}^{{i}\theta_{{i}} } =\mathrm{0} \\ $$$${m}_{\mathrm{5}} {e}^{{i}\theta_{\mathrm{5}} } =−\left(\underset{{i}} {\sum}{m}_{{i}} \rho_{\mathrm{1}} {e}^{{i}\theta_{{i}} } \right)/\rho_{\mathrm{5}} \\ $$$${m}_{\mathrm{5}} {cos}\left(\theta_{\mathrm{5}} \right)=−\left(\Sigma{m}_{{i}} \rho_{{i}} {cos}\left(\theta_{{i}} \right)\right)/\rho_{\mathrm{5}} \\ $$$${m}_{\mathrm{5}} {sin}\left(\theta_{\mathrm{5}} \right)=−\left(\Sigma{m}_{{i}} \rho_{{i}} {sin}\left(\theta_{{i}} \right)\right)/\rho_{\mathrm{5}} \\ $$$${m}_{\mathrm{5}} {cos}\left(\theta_{\mathrm{5}} \right)={A} \\ $$$${m}_{\mathrm{5}} {sin}\left(\theta_{\mathrm{5}} \right)={B} \\ $$$${tan}\left(\theta_{\mathrm{5}} \right)=\frac{{B}}{{A}} \\ $$$${m}_{\mathrm{5}} =\frac{{A}}{{cos}\left(\theta_{\mathrm{5}} \right)}=\frac{{A}}{\:\sqrt{\frac{\mathrm{1}}{\frac{{B}^{\mathrm{2}} }{{A}^{\mathrm{2}} }+\mathrm{1}}}}=\frac{{A}^{\mathrm{2}} }{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }} \\ $$

Commented by BHOOPENDRA last updated on 26/Apr/21

thankyou

$${thankyou} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com