
Question and Answers Forum
Question Number 139427 by Fikret last updated on 26/Apr/21
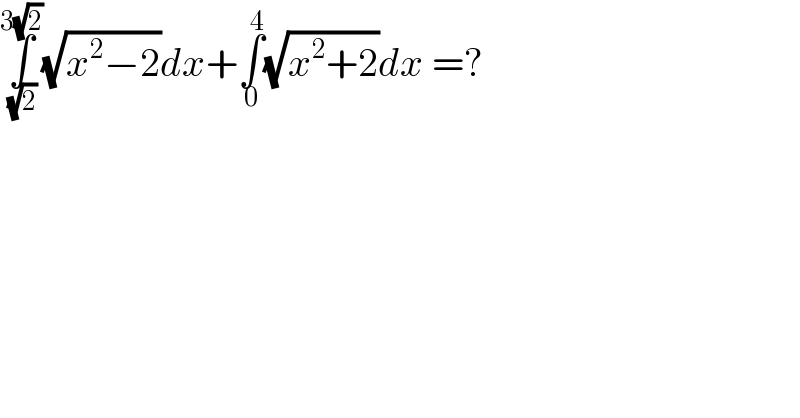
Answered by MJS_new last updated on 27/Apr/21
![∫(√(x^2 −2))dx= [t=((x+(√(x^2 −2)))/( (√2))) → dx=((√(2(x^2 −2)))/(x+(√(x^2 −2))))dt] =∫((t/2)−(1/t)+(1/(2t^3 )))dt= =((t^4 −1)/(4t^2 ))−ln t = =(1/2)x(√(x^2 −2))−ln (x+(√(x^2 −2))) +C_1 ∫(√(x^2 +2))dx= [u=((x+(√(x^2 +2)))/( (√2))) → dx=((√(2(x^2 +2)))/(x+(√(x^2 +2))))du] =∫((u/2)+(1/u)+(1/(2u^3 )))dt= =((u^4 −1)/(4u^2 ))+ln u = =(1/2)x(√(x^2 +2))−ln (x+(√(x^2 +2))) +C_2 ⇒ answer is 12(√2)](Q139430.png)
Answered by mathmax by abdo last updated on 27/Apr/21
![I = H +K H =∫_(√2) ^(3(√2)) (√(x^2 −2))dx =_(x=(√2)cht→t=argch((x/( (√2))))) ∫_(argch(1)) ^(argch(3)) (√2)sht .(√2)sht dt =2 ∫_0 ^(ln(3+2(√2))) ((ch(2t)−1)/2)dt=[((sh(2t))/2)]_0 ^(ln(3+2(√2))) −ln(3+2(√2)) =(1/2)[((e^(2t) −e^(−2t) )/2)]_0 ^(ln(3+2(√2))) −ln(3+2(√2)) =(1/4){(3+2(√2))^2 −(3+2(√2))^(−2) } −ln(3+2(√2)) K =∫_0 ^4 (√(x^2 +2))dx =_(x=(√2)sh(t)→t=argsh((x/( (√2))))) ∫_0 ^(argsh((4/( (√2))))) (√2)ch(t)(√2)ch(t) =2 ∫_0 ^(ln((4/( (√2)))+3)) ((1+ch(2t))/2)dt =ln((4/( (√2)))+3)+[(1/2)sh(2t)]_0 ^(ln(3+2(√2))) =ln(3+2(√2))+(1/4){(3+2(√2))^2 −(3+2(√2))^(−2) } ⇒ I =(1/2){(3+2(√2))^2 −(3+2(√2))^(−2) }−ln(3+2(√2))](Q139431.png)
| ||
Question and Answers Forum | ||
Question Number 139427 by Fikret last updated on 26/Apr/21 | ||
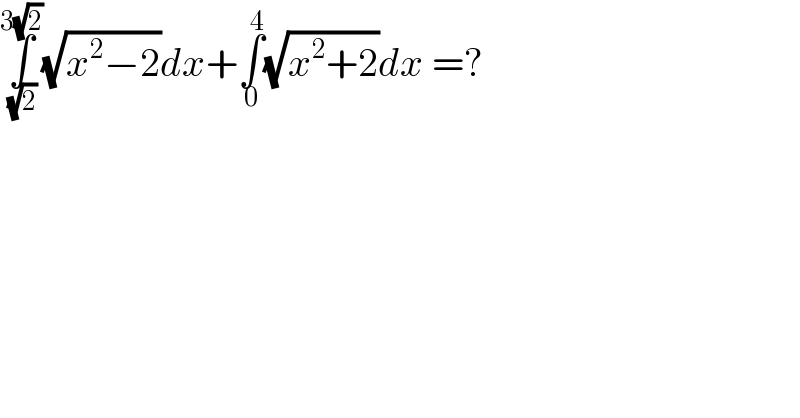 | ||
Answered by MJS_new last updated on 27/Apr/21 | ||
![∫(√(x^2 −2))dx= [t=((x+(√(x^2 −2)))/( (√2))) → dx=((√(2(x^2 −2)))/(x+(√(x^2 −2))))dt] =∫((t/2)−(1/t)+(1/(2t^3 )))dt= =((t^4 −1)/(4t^2 ))−ln t = =(1/2)x(√(x^2 −2))−ln (x+(√(x^2 −2))) +C_1 ∫(√(x^2 +2))dx= [u=((x+(√(x^2 +2)))/( (√2))) → dx=((√(2(x^2 +2)))/(x+(√(x^2 +2))))du] =∫((u/2)+(1/u)+(1/(2u^3 )))dt= =((u^4 −1)/(4u^2 ))+ln u = =(1/2)x(√(x^2 +2))−ln (x+(√(x^2 +2))) +C_2 ⇒ answer is 12(√2)](Q139430.png) | ||
| ||
Answered by mathmax by abdo last updated on 27/Apr/21 | ||
![I = H +K H =∫_(√2) ^(3(√2)) (√(x^2 −2))dx =_(x=(√2)cht→t=argch((x/( (√2))))) ∫_(argch(1)) ^(argch(3)) (√2)sht .(√2)sht dt =2 ∫_0 ^(ln(3+2(√2))) ((ch(2t)−1)/2)dt=[((sh(2t))/2)]_0 ^(ln(3+2(√2))) −ln(3+2(√2)) =(1/2)[((e^(2t) −e^(−2t) )/2)]_0 ^(ln(3+2(√2))) −ln(3+2(√2)) =(1/4){(3+2(√2))^2 −(3+2(√2))^(−2) } −ln(3+2(√2)) K =∫_0 ^4 (√(x^2 +2))dx =_(x=(√2)sh(t)→t=argsh((x/( (√2))))) ∫_0 ^(argsh((4/( (√2))))) (√2)ch(t)(√2)ch(t) =2 ∫_0 ^(ln((4/( (√2)))+3)) ((1+ch(2t))/2)dt =ln((4/( (√2)))+3)+[(1/2)sh(2t)]_0 ^(ln(3+2(√2))) =ln(3+2(√2))+(1/4){(3+2(√2))^2 −(3+2(√2))^(−2) } ⇒ I =(1/2){(3+2(√2))^2 −(3+2(√2))^(−2) }−ln(3+2(√2))](Q139431.png) | ||
| ||