Question Number 139738 by mathsuji last updated on 30/Apr/21
$$\underset{{n}\rightarrow\infty} {{lim}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{{n}\centerdot{x}^{{n}} }{\mathrm{2}+{x}^{{n}} }\:{dx}=? \\ $$
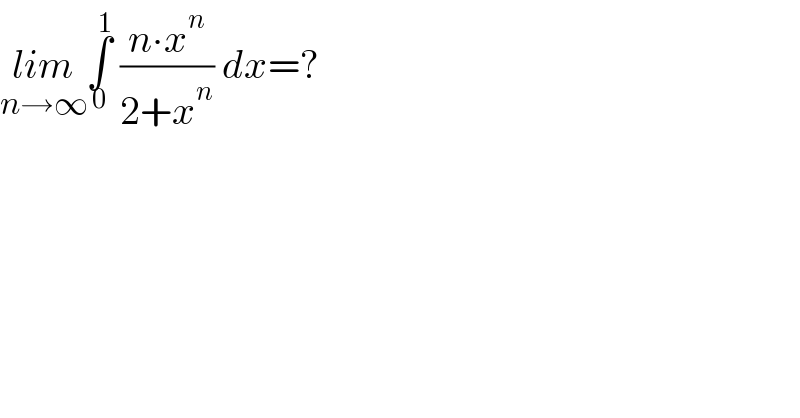
Answered by mindispower last updated on 01/May/21
![∫_0 ^1 ((nx^n )/(2+x^n ))dx=∫_0 ^1 x.((d(2+x^n ))/(2+x^n )) =[xln(2+x^n )]_0 ^1 −∫_0 ^1 ln(2+x^n )dx =ln(3)−∫_0 ^1 ln(2(1+(x^n /2)))dx =ln((3/2))−∫_0 ^1 ln(1+(x^n /2))dx 0≤ln(1+x)≤x...∀x∈[0,∞[ proof 0≤(1/(1+x))≤1⇒0≤∫_0 ^x (1/(1+t))≤∫_0 ^x 1dt ⇔0≤ln(1+x)≤x proved ⇒0≤ln(1+(x^n /2))≤(x^n /2)⇒0≤An=∫_0 ^1 ln(1+(x^n /2))dx≤∫_0 ^1 (x^n /2) ⇔0≤A_n ≤(1/(2(n+1)))⇒lim_(n→∞) An=0 ⇒lim_(n→∞) ∫_0 ^1 ((nx^n )/(1+x^n ))dx=lim_(n→∞) ln((3/2))+A_n =ln((3/2))](Q139748.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{nx}^{{n}} }{\mathrm{2}+{x}^{{n}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}.\frac{{d}\left(\mathrm{2}+{x}^{{n}} \right)}{\mathrm{2}+{x}^{{n}} } \\ $$$$=\left[{xln}\left(\mathrm{2}+{x}^{{n}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{2}+{x}^{{n}} \right){dx} \\ $$$$={ln}\left(\mathrm{3}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{2}\left(\mathrm{1}+\frac{{x}^{{n}} }{\mathrm{2}}\right)\right){dx} \\ $$$$={ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+\frac{{x}^{{n}} }{\mathrm{2}}\right){dx} \\ $$$$\mathrm{0}\leqslant{ln}\left(\mathrm{1}+{x}\right)\leqslant{x}...\forall{x}\in\left[\mathrm{0},\infty\left[\right.\right. \\ $$$${proof}\:\:\:\:\mathrm{0}\leqslant\frac{\mathrm{1}}{\mathrm{1}+{x}}\leqslant\mathrm{1}\Rightarrow\mathrm{0}\leqslant\int_{\mathrm{0}} ^{{x}} \frac{\mathrm{1}}{\mathrm{1}+{t}}\leqslant\int_{\mathrm{0}} ^{{x}} \mathrm{1}{dt} \\ $$$$\Leftrightarrow\mathrm{0}\leqslant{ln}\left(\mathrm{1}+{x}\right)\leqslant{x} \\ $$$${proved} \\ $$$$\Rightarrow\mathrm{0}\leqslant{ln}\left(\mathrm{1}+\frac{{x}^{{n}} }{\mathrm{2}}\right)\leqslant\frac{{x}^{{n}} }{\mathrm{2}}\Rightarrow\mathrm{0}\leqslant{An}=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+\frac{{x}^{{n}} }{\mathrm{2}}\right){dx}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}} }{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{0}\leqslant{A}_{{n}} \leqslant\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}{An}=\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{nx}^{{n}} }{\mathrm{1}+{x}^{{n}} }{dx}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\mathrm{A}_{{n}} ={ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$
Commented by mathsuji last updated on 02/May/21
$${thank}\:{you}\:{very}\:{much}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 01/May/21
![U_n =∫_0 ^1 ((nx^n )/(2+x^n ))dx ⇒U_n =n ∫_0 ^1 (x^n /(2+x^n ))dx =_(x^n =t) n ∫_0 ^1 (t/(2+t))×(1/n)t^((1/n)−1) dt =∫_0 ^1 ((t^(1/n) )/(2+t))dt ⇒lim_(n→+∞) U_n =lim_(n→+∞) ∫_0 ^1 (t^(1/n) /(2+t))dt =∫_0 ^1 (dt/(2+t)) =[ln(t+2)]_0 ^1 =ln(3)−ln(2)](Q139760.png)
$$\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{nx}^{\mathrm{n}} }{\mathrm{2}+\mathrm{x}^{\mathrm{n}} }\mathrm{dx}\:\Rightarrow\mathrm{U}_{\mathrm{n}} =\mathrm{n}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{2}+\mathrm{x}^{\mathrm{n}} }\mathrm{dx}\:=_{\mathrm{x}^{\mathrm{n}} =\mathrm{t}} \:\:\:\mathrm{n}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}}{\mathrm{2}+\mathrm{t}}×\frac{\mathrm{1}}{\mathrm{n}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \:\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}} \:}{\mathrm{2}+\mathrm{t}}\mathrm{dt}\:\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{U}_{\mathrm{n}} =\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{n}}} }{\mathrm{2}+\mathrm{t}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{2}+\mathrm{t}} \\ $$$$=\left[\mathrm{ln}\left(\mathrm{t}+\mathrm{2}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{ln}\left(\mathrm{3}\right)−\mathrm{ln}\left(\mathrm{2}\right) \\ $$
Commented by mathsuji last updated on 02/May/21
$${thank}\:{you}\:{very}\:{much}\:{sir} \\ $$