Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 139771 by Engr_Jidda last updated on 01/May/21

Commented by mohammad17 last updated on 01/May/21

yes sir realy im sory can you solve this?

$${yes}\:{sir}\:{realy}\:{im}\:{sory}\:{can}\:{you}\:{solve}\:{this}? \\ $$

Commented by mr W last updated on 01/May/21

take care! (3)^(1/(1/2)) =3^2 ≠3^(1/2)

$${take}\:{care}! \\ $$$$\sqrt[{\frac{\mathrm{1}}{\mathrm{2}}}]{\mathrm{3}}=\mathrm{3}^{\mathrm{2}} \neq\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$

Commented by mohammad17 last updated on 01/May/21

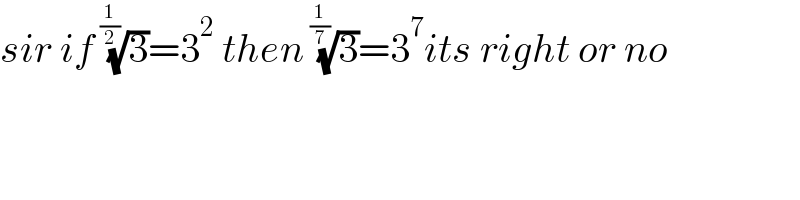
sir if (3)^(1/(1/2)) =3^2 then (3)^(1/(1/7)) =3^7 its right or no

$${sir}\:{if}\:\sqrt[{\frac{\mathrm{1}}{\mathrm{2}}}]{\mathrm{3}}=\mathrm{3}^{\mathrm{2}} \:{then}\:\sqrt[{\frac{\mathrm{1}}{\mathrm{7}}}]{\mathrm{3}}=\mathrm{3}^{\mathrm{7}} {its}\:{right}\:{or}\:{no} \\ $$

Commented by mr W last updated on 01/May/21

yes. it′s right.

$${yes}.\:{it}'{s}\:{right}. \\ $$

Commented by mohammad17 last updated on 01/May/21

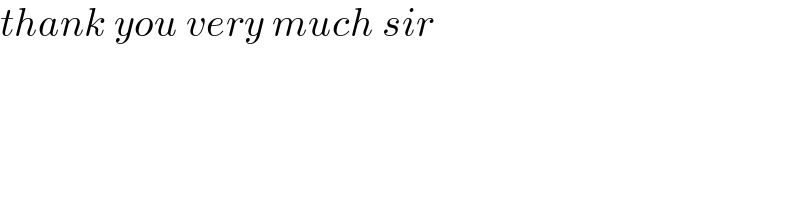
thank you very much sir

$${thank}\:{you}\:{very}\:{much}\:{sir}\: \\ $$

Answered by mr W last updated on 01/May/21

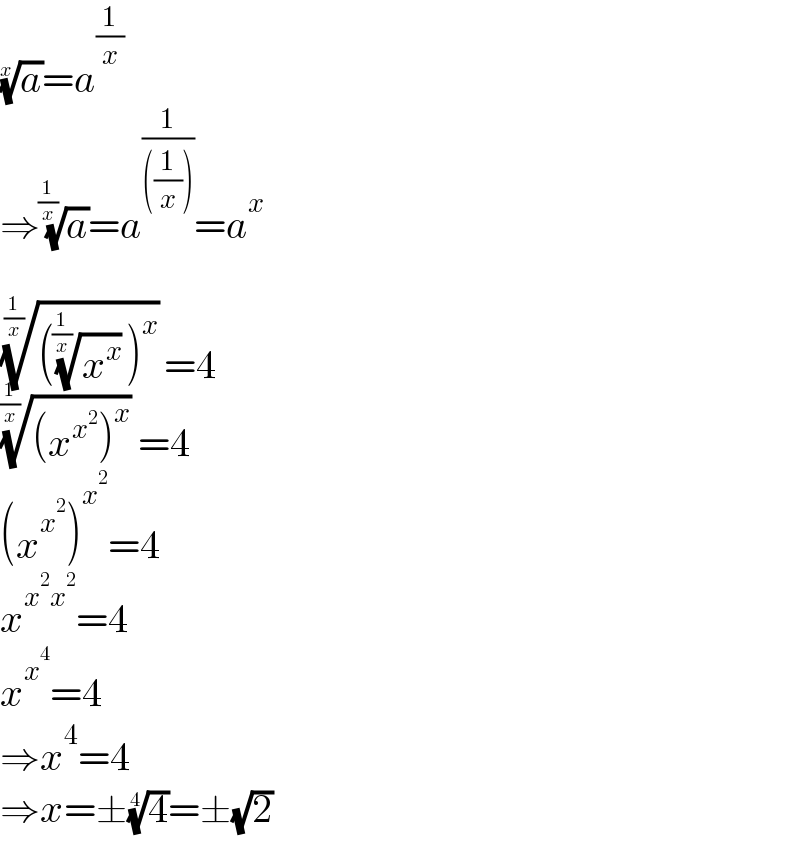
(a)^(1/x) =a^(1/x) ⇒(a)^(1/(1/x)) =a^(1/(((1/x)))) =a^x ((((x^x )^(1/(1/x)) )^x ))^(1/(1/x)) =4 (((x^x^2 )^x ))^(1/(1/x)) =4 (x^x^2 )^x^2 =4 x^(x^2 x^2 ) =4 x^x^4 =4 ⇒x^4 =4 ⇒x=±(4)^(1/4) =±(√2)

$$\sqrt[{{x}}]{{a}}={a}^{\frac{\mathrm{1}}{{x}}} \\ $$$$\Rightarrow\sqrt[{\frac{\mathrm{1}}{{x}}}]{{a}}={a}^{\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{{x}}\right)}} ={a}^{{x}} \\ $$$$ \\ $$$$\sqrt[{\frac{\mathrm{1}}{{x}}}]{\left(\sqrt[{\frac{\mathrm{1}}{{x}}}]{{x}^{{x}} }\right)^{{x}} }=\mathrm{4} \\ $$$$\sqrt[{\frac{\mathrm{1}}{{x}}}]{\left({x}^{{x}^{\mathrm{2}} } \right)^{{x}} }=\mathrm{4} \\ $$$$\left({x}^{{x}^{\mathrm{2}} } \right)^{{x}^{\mathrm{2}} } =\mathrm{4} \\ $$$${x}^{{x}^{\mathrm{2}} {x}^{\mathrm{2}} } =\mathrm{4} \\ $$$${x}^{{x}^{\mathrm{4}} } =\mathrm{4} \\ $$$$\Rightarrow{x}^{\mathrm{4}} =\mathrm{4} \\ $$$$\Rightarrow{x}=\pm\sqrt[{\mathrm{4}}]{\mathrm{4}}=\pm\sqrt{\mathrm{2}} \\ $$

Commented by Ankushkumarparcha last updated on 01/May/21

if u use power tower then this equation has no solution ∵ range R ∈ [(1/e) , e]

$${if}\:{u}\:{use}\:{power}\:{tower}\:{then}\:{this}\:{equation}\:{has}\:{no}\:{solution} \\ $$$$\because\:{range}\:{R}\:\in\:\left[\frac{\mathrm{1}}{{e}}\:,\:{e}\right] \\ $$

Commented by mr W last updated on 01/May/21

i didn′t use power tower. the original equation is equivalent to x^x^4 =4. and eqn. x^x^4 =a has always solution if a≥≈0.9121

$${i}\:{didn}'{t}\:{use}\:{power}\:{tower}. \\ $$$${the}\:{original}\:{equation}\:{is}\:{equivalent}\:{to} \\ $$$${x}^{{x}^{\mathrm{4}} } =\mathrm{4}. \\ $$$${and}\:{eqn}.\:{x}^{{x}^{\mathrm{4}} } ={a}\:{has}\:{always}\:{solution}\:{if} \\ $$$${a}\geqslant\approx\mathrm{0}.\mathrm{9121} \\ $$

Answered by Ankushkumarparcha last updated on 01/May/21

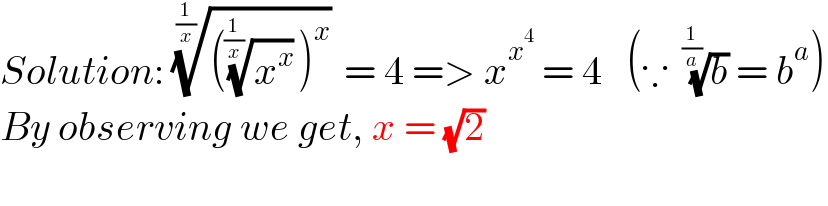
Solution: ((((x^x )^(1/(1/x)) )^x ))^(1/(1/x)) = 4 => x^x^4 = 4 (∵ (b)^(1/(1/a)) = b^a ) By observing we get, x = (√2)

$${Solution}:\:\sqrt[{\frac{\mathrm{1}}{{x}}}]{\left(\sqrt[{\frac{\mathrm{1}}{{x}}}]{{x}^{{x}} }\right)^{{x}} }\:=\:\mathrm{4}\:=>\:{x}^{{x}^{\mathrm{4}} } \:=\:\mathrm{4}\:\:\:\left(\because\:\:\sqrt[{\frac{\mathrm{1}}{{a}}}]{{b}}\:=\:{b}^{{a}} \right) \\ $$$${By}\:{observing}\:{we}\:{get},\:{x}\:=\:\sqrt{\mathrm{2}}\: \\ $$$$ \\ $$

Commented by mr W last updated on 01/May/21

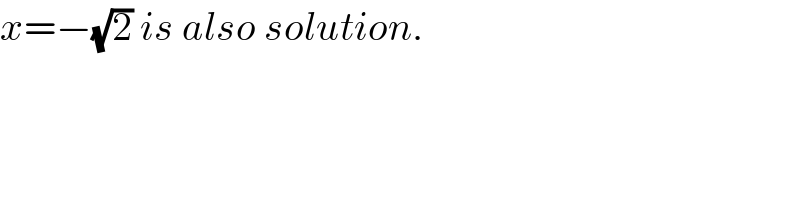
x=−(√2) is also solution.

$${x}=−\sqrt{\mathrm{2}}\:{is}\:{also}\:{solution}. \\ $$

Answered by Ar Brandon last updated on 01/May/21

x^x^4 =4⇒x^4 lnx=ln4 ⇒4x^4 lnx=4ln4 ⇒4lnx∙e^(4lnx) =ln4∙e^(ln4) ⇒W_0 (4lnx)=W_0 (ln4) ⇒4lnx=ln4⇒x^4 =4⇒x=±(√2)

$$\mathrm{x}^{\mathrm{x}^{\mathrm{4}} } =\mathrm{4}\Rightarrow\mathrm{x}^{\mathrm{4}} \mathrm{lnx}=\mathrm{ln4} \\ $$$$\Rightarrow\mathrm{4x}^{\mathrm{4}} \mathrm{lnx}=\mathrm{4ln4} \\ $$$$\Rightarrow\mathrm{4lnx}\centerdot\mathrm{e}^{\mathrm{4lnx}} =\mathrm{ln4}\centerdot\mathrm{e}^{\mathrm{ln4}} \\ $$$$\Rightarrow\mathrm{W}_{\mathrm{0}} \left(\mathrm{4lnx}\right)=\mathrm{W}_{\mathrm{0}} \left(\mathrm{ln4}\right) \\ $$$$\Rightarrow\mathrm{4lnx}=\mathrm{ln4}\Rightarrow\mathrm{x}^{\mathrm{4}} =\mathrm{4}\Rightarrow\mathrm{x}=\pm\sqrt{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com