𝛗:=∫_0 ^( 1) (√x) ln((1/(1−x)))dx solution: 𝛗:= ∫_0 ^( 1) (√x) Σ_(n=1) ^∞ (x^n /n) dx :=Σ_(n=1) ^∞ (1/n)∫_0 ^( 1) x^(n+(1/2)) dx := Σ_(n=1) ^∞ (1/(n(n+(3/2)))) = (2/3)Σ_(n=1) ^∞ ((1/n)−(1/(n+(3/2)))) :=(2/3){γ −γ+Σ_(n=1) ^∞ ((1/n)−(1/(n+(3/2)))) } := (2/3) γ +(2/3) ψ(1+(3/2))=(2/3) γ +(2/3)((2/3)+ψ((3/2))) :=(2/3) γ +(4/9) +(2/3)(2+ψ((1/2))) :=(2/3) γ +((16)/9) −(2/3) γ−(4/3) ln(2) :=((16)/9) −(4/3) ln(2) .....✓


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 139811 by mnjuly1970 last updated on 01/May/21
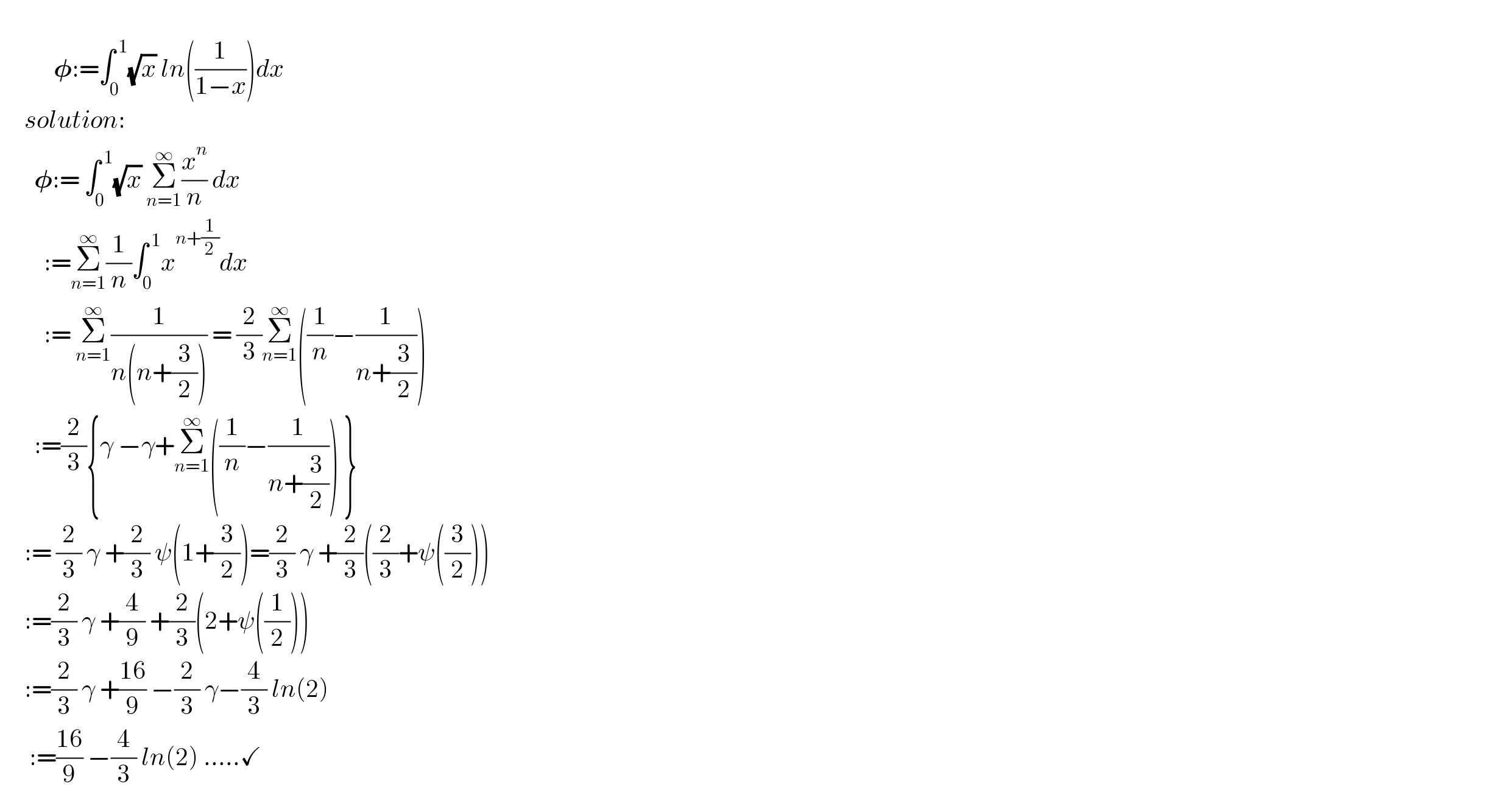
$𝛗:=∫_0 ^( 1) (√x) ln((1/(1−x)))dx solution: 𝛗:= ∫_0 ^( 1) (√x) Σ_(n=1) ^∞ (x^n /n) dx :=Σ_(n=1) ^∞ (1/n)∫_0 ^( 1) x^(n+(1/2)) dx := Σ_(n=1) ^∞ (1/(n(n+(3/2)))) = (2/3)Σ_(n=1) ^∞ ((1/n)−(1/(n+(3/2)))) :=(2/3){γ −γ+Σ_(n=1) ^∞ ((1/n)−(1/(n+(3/2)))) } := (2/3) γ +(2/3) ψ(1+(3/2))=(2/3) γ +(2/3)((2/3)+ψ((3/2))) :=(2/3) γ +(4/9) +(2/3)(2+ψ((1/2))) :=(2/3) γ +((16)/9) −(2/3) γ−(4/3) ln(2) :=((16)/9) −(4/3) ln(2) .....✓$
$ϕ := \int_{0}^{1} \sqrt{x} l n (\frac{1}{1 - x}) d x$ $s o l u t i o n :$ $ϕ := \int_{0}^{1} \sqrt{x} \underset{n = 1}{\sum^{\infty}} \frac{x^{n}}{n} d x$ $:= \underset{n = 1}{\sum^{\infty}} \frac{1}{n} \int_{0}^{1} x^{n + \frac{1}{2}} d x$ $:= \underset{n = 1}{\sum^{\infty}} \frac{1}{n (n + \frac{3}{2})} = \frac{2}{3} \underset{n = 1}{\sum^{\infty}} (\frac{1}{n} - \frac{1}{n + \frac{3}{2}})$ $:= \frac{2}{3} {γ - γ + \underset{n = 1}{\sum^{\infty}} (\frac{1}{n} - \frac{1}{n + \frac{3}{2}})}$ $:= \frac{2}{3} γ + \frac{2}{3} ψ (1 + \frac{3}{2}) = \frac{2}{3} γ + \frac{2}{3} (\frac{2}{3} + ψ (\frac{3}{2}))$ $:= \frac{2}{3} γ + \frac{4}{9} + \frac{2}{3} (2 + ψ (\frac{1}{2}))$ $:= \frac{2}{3} γ + \frac{16}{9} - \frac{2}{3} γ - \frac{4}{3} l n (2)$ $:= \frac{16}{9} - \frac{4}{3} l n (2) . . . . . ✓$
	Answered by mathmax by abdo last updated on 01/May/21
	$Φ=∫_0 ^1 (√x)log((1/(1−x)))dx ⇒Φ=−∫_0 ^1 (√x)log(1−x)dx =_((√x)=t) −∫_0 ^1 t log(1−t^2 )(2t)dt =−2∫_0 ^1 t^2 log(1−t^2 )dt =−2{ [((t^3 −1)/3)log(1−t^2 )]_0 ^1 −∫_0 ^1 ((t^3 −1)/3)×((−2t)/(1−t^2 ))dt} =−(4/3) ∫_0 ^1 ((t^4 −t)/(1−t^2 ))dt =(4/3)∫_0 ^1 ((t(t^3 −1))/((t−1)(t+1)))dt =(4/3) ∫_0 ^1 ((t(t^2 +t+1))/(t+1))dt =(4/3)∫_0 ^1 ((t^3 +t^2 +t)/(t+1))dt =_(t+1=y) (4/3)∫_1 ^2 (((y−1)^3 +(y−1)^2 +y−1)/y)dy =(4/3)∫_1 ^2 ((y^3 −3y^2 +3y−1+y^2 −2y+1+y−1)/y)dy =(4/3)∫_1 ^2 ((y^3 −2y^2 +2y−1)/y)dy =(4/3)∫_1 ^2 (y^2 −2y+2−(1/y))dy =(4/3)[(y^3 /3)−y^2 +2y−log∣y∣]_1 ^2 =(4/3){(8/3)−4+4−log2−(1/3)+1−2} =(4/3){(7/3)−1−log2} =(4/3)((4/3)−log2) =((16)/9)−(4/3)log2$
	$Φ = \int_{0}^{1} \sqrt{x} \log (\frac{1}{1 - x}) dx \Rightarrow Φ = - \int_{0}^{1} \sqrt{x} \log (1 - x) dx$ $=_{\sqrt{x} = t} - \int_{0}^{1} t \log (1 - t^{2}) (2 t) dt$ $= - 2 \int_{0}^{1} t^{2} \log (1 - t^{2}) dt$ $= - 2 {{[\frac{t^{3} - 1}{3} \log (1 - t^{2})]}_{0}^{1} - \int_{0}^{1} \frac{t^{3} - 1}{3} \times \frac{- 2 t}{1 - t^{2}} dt}$ $= - \frac{4}{3} \int_{0}^{1} \frac{t^{4} - t}{1 - t^{2}} dt = \frac{4}{3} \int_{0}^{1} \frac{t (t^{3} - 1)}{(t - 1) (t + 1)} dt$ $= \frac{4}{3} \int_{0}^{1} \frac{t (t^{2} + t + 1)}{t + 1} dt = \frac{4}{3} \int_{0}^{1} \frac{t^{3} + t^{2} + t}{t + 1} dt$ $=_{t + 1 = y} \frac{4}{3} \int_{1}^{2} \frac{{(y - 1)}^{3} + {(y - 1)}^{2} + y - 1}{y} dy$ $= \frac{4}{3} \int_{1}^{2} \frac{y^{3} - {3 y}^{2} + 3 y - 1 + y^{2} - 2 y + 1 + y - 1}{y} dy$ $= \frac{4}{3} \int_{1}^{2} \frac{y^{3} - {2 y}^{2} + 2 y - 1}{y} dy$ $= \frac{4}{3} \int_{1}^{2} (y^{2} - 2 y + 2 - \frac{1}{y}) dy$ $= \frac{4}{3} {[\frac{y^{3}}{3} - y^{2} + 2 y - \log ∣ y ∣]}_{1}^{2}$ $= \frac{4}{3} {\frac{8}{3} - 4 + 4 - \log 2 - \frac{1}{3} + 1 - 2}$ $= \frac{4}{3} {\frac{7}{3} - 1 - \log 2} = \frac{4}{3} (\frac{4}{3} - \log 2) = \frac{16}{9} - \frac{4}{3} \log 2$
	Commented by mnjuly1970 last updated on 01/May/21

	$t h x s i r m a x . . .$
	Commented by mathmax by abdo last updated on 02/May/21

	$you are welcome sir$
	Answered by Ar Brandon last updated on 16/May/21
	$φ=∫_0 ^1 (√x)ln((1/(1−x)))dx=−∫_0 ^1 (√x)ln(1−x)dx ∫_0 ^1 x^(m−1) (1−x)^(n−1) dx=β(m,n)=((Γ(m)Γ(n))/(Γ(m+n))) lnβ(m,n)=lnΓ(m)+lnΓ(n)−lnΓ(m+n) (1/(β(m,n)))∙((∂β(m,n))/∂n)=ψ(n)−ψ(m+n) ⇒((∂β((3/2),1))/∂n)=β((3/2),1){ψ(1)−ψ((5/2))} =((Γ((3/2)))/(Γ((5/2)))){−γ−((2/3)+2−γ−2ln2)} φ=−(2/3)(2ln2−(8/3))=((16)/9)−((4ln2)/3)$
	$ϕ = \int_{0}^{1} \sqrt{x} \ln (\frac{1}{1 - x}) dx = - \int_{0}^{1} \sqrt{x} \ln (1 - x) dx$ $\int_{0}^{1} x^{m - 1} {(1 - x)}^{n - 1} dx = β (m, n) = \frac{Γ (m) Γ (n)}{Γ (m + n)}$ $\ln β (m, n) = \ln Γ (m) + \ln Γ (n) - \ln Γ (m + n)$ $\frac{1}{β (m, n)} \cdot \frac{\partial β (m, n)}{\partial n} = ψ (n) - ψ (m + n)$ $\Rightarrow \frac{\partial β (\frac{3}{2}, 1)}{\partial n} = β (\frac{3}{2}, 1) {ψ (1) - ψ (\frac{5}{2})}$ $= \frac{Γ (\frac{3}{2})}{Γ (\frac{5}{2})} {- γ - (\frac{2}{3} + 2 - γ - 2 \ln 2)}$ $ϕ = - \frac{2}{3} (2 \ln 2 - \frac{8}{3}) = \frac{16}{9} - \frac{4 \ln 2}{3}$
	Commented by mnjuly1970 last updated on 01/May/21

	$g r a t e f u l m r b r a n d o n . . .$
	Commented by SLVR last updated on 01/May/21

	$c o u l d y o u e x p l a i n w h a t ψ (1) ? ψ (5 / 2)$ $T h a n k s m r . B r a n d o n s i r$
	Commented by Ar Brandon last updated on 01/May/21

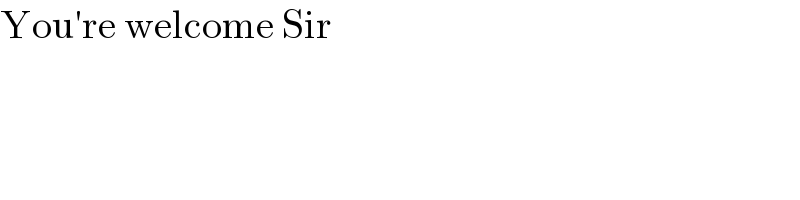
	${You}^{'} re welcome Sir$
	Commented by Ar Brandon last updated on 01/May/21

	$Γ^{'} (x) = Γ (x) ψ (x) \Rightarrow \frac{Γ^{'} (x)}{Γ (x)} = ψ (x)$ $ψ (s + 1) = \frac{1}{s} + ψ (s), ψ (\frac{1}{2}) = - γ - 2 \ln 2$ $ψ (x) = - γ + \underset{n = 0}{\sum^{\infty}} (\frac{1}{n + 1} - \frac{1}{n + x}) \Rightarrow ψ (1) = - γ$ $ψ (x) represents digamma function .$
	Commented by SLVR last updated on 01/May/21

	$S o . . . . k i n d y o u . . s i r G r e a t . . . e x p l a n a t i o n$ $G o d . . . b l e s s y o u f o r e v e r$
	Commented by Ar Brandon last updated on 01/May/21

	$Thanks!$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum