
Question and Answers Forum
Question Number 139826 by qaz last updated on 01/May/21
![Σ_(n=0) ^∞ ((sin [(n−1)x])/4^(n+1) )=?](Q139826.png)
Answered by mnjuly1970 last updated on 01/May/21
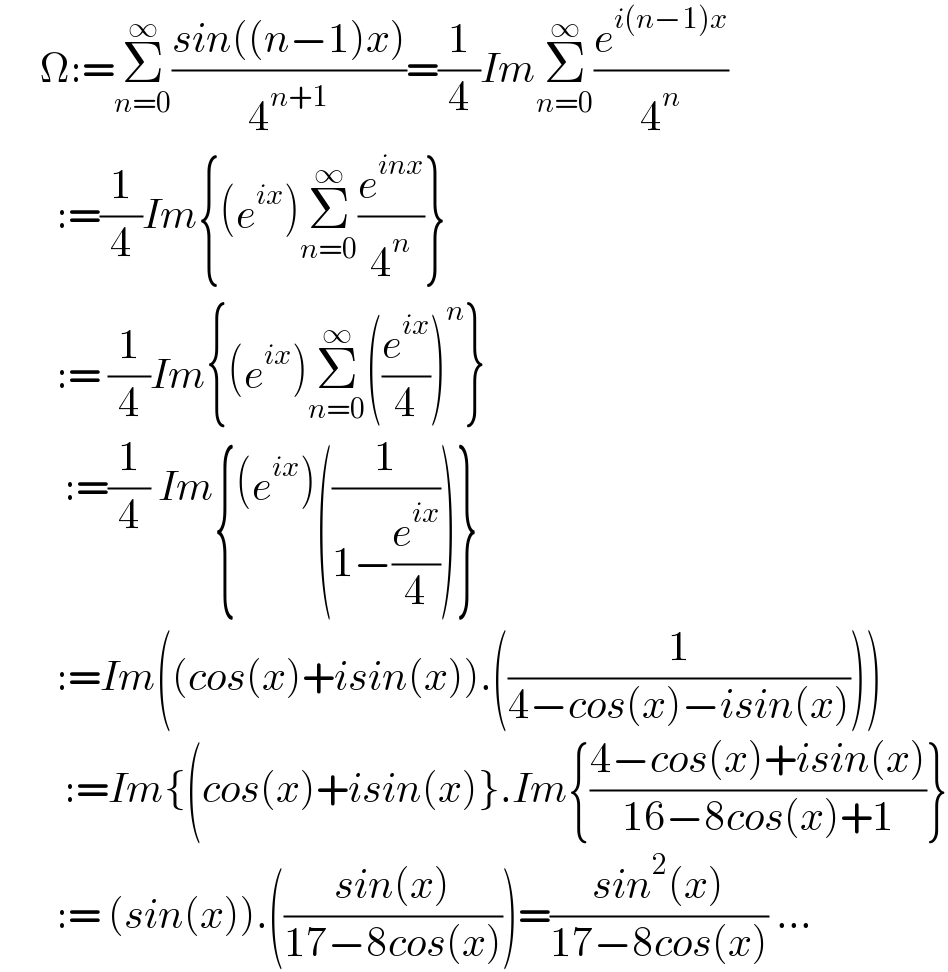
Answered by Dwaipayan Shikari last updated on 01/May/21
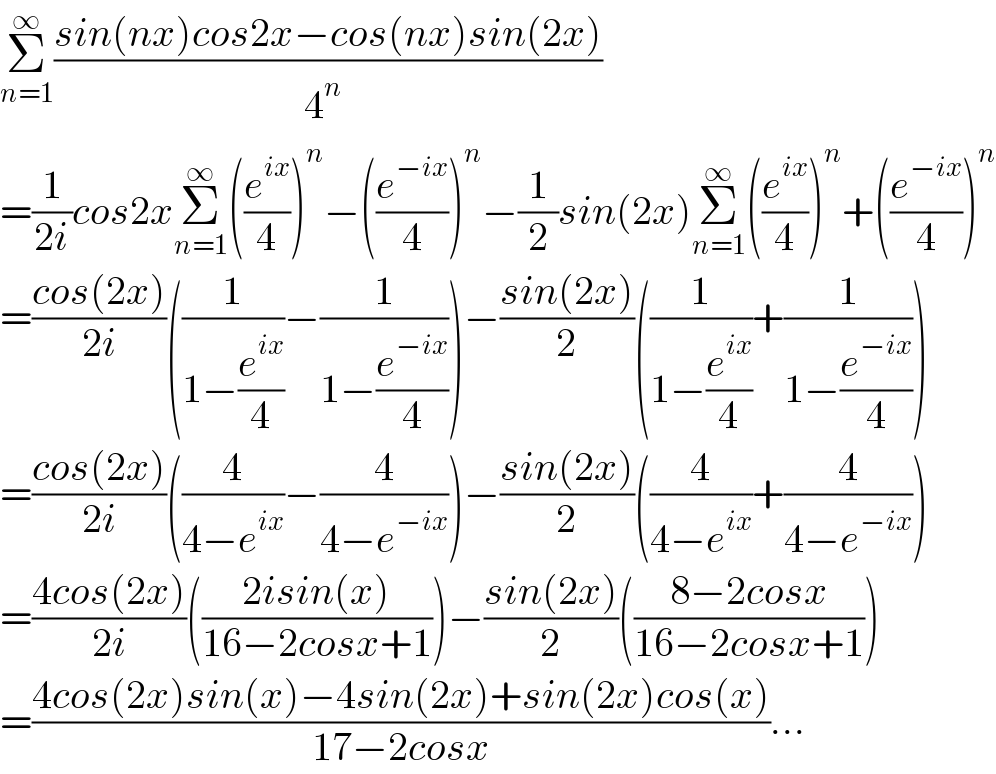
| ||
Question and Answers Forum | ||
Question Number 139826 by qaz last updated on 01/May/21 | ||
![Σ_(n=0) ^∞ ((sin [(n−1)x])/4^(n+1) )=?](Q139826.png) | ||
Answered by mnjuly1970 last updated on 01/May/21 | ||
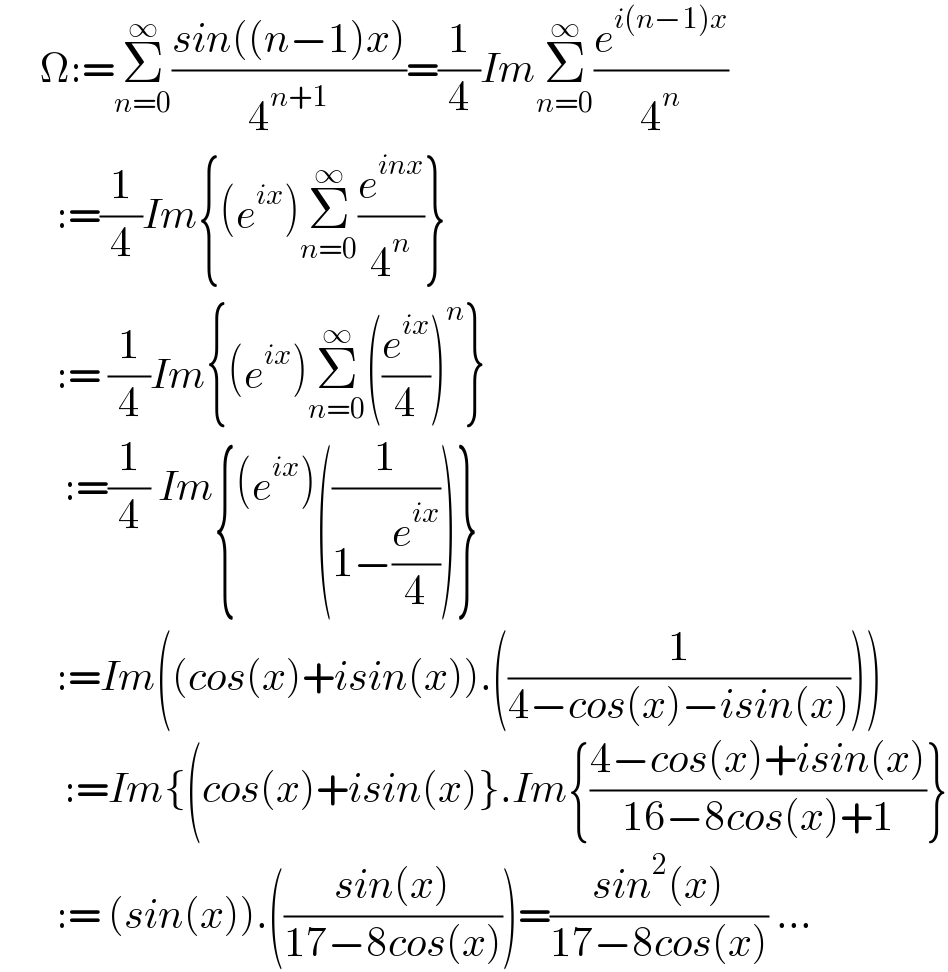 | ||
| ||
Answered by Dwaipayan Shikari last updated on 01/May/21 | ||
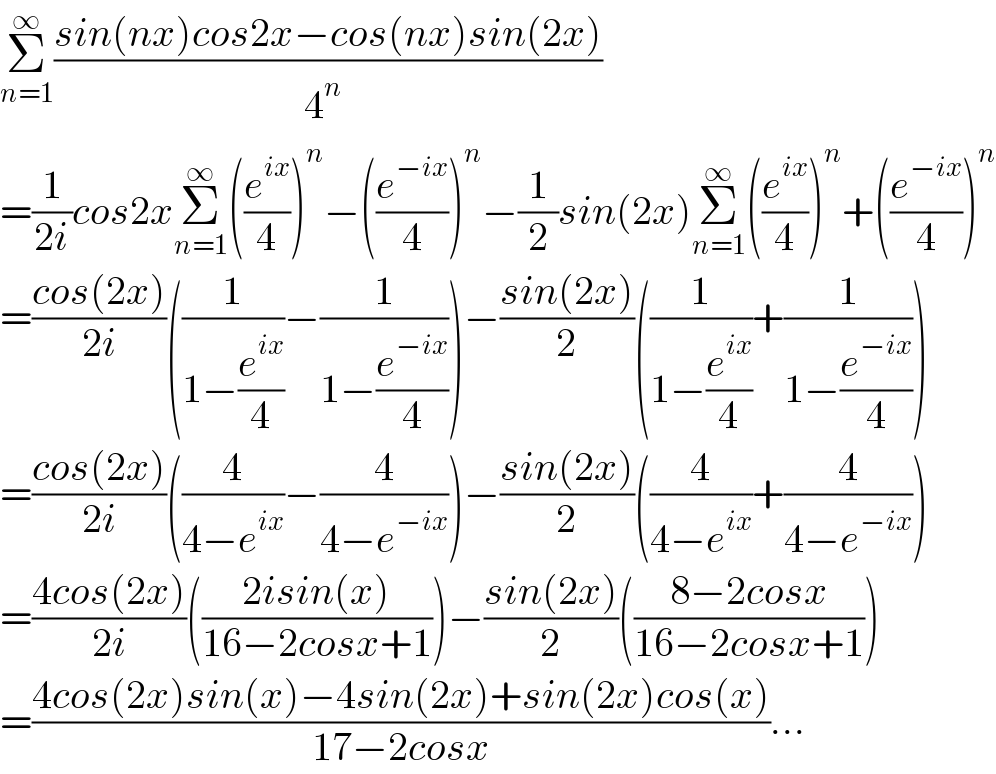 | ||
| ||