
Question and Answers Forum
Question Number 139878 by bramlexs22 last updated on 02/May/21
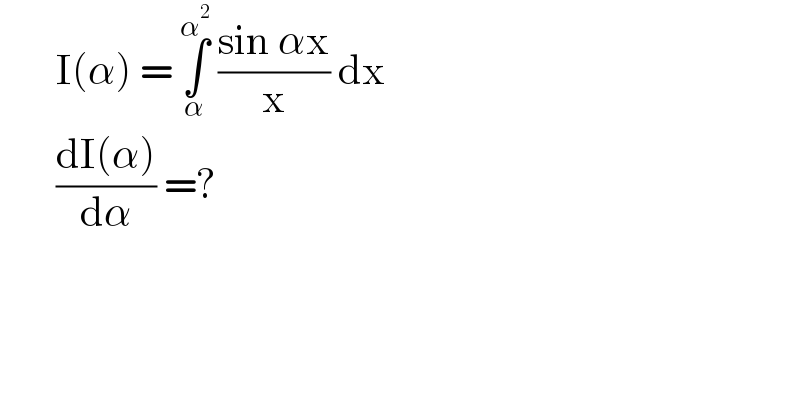
Answered by EDWIN88 last updated on 02/May/21
![(dI/dα) = ∫_α ^α^2 (∂/∂α)(((sin αx)/x)) dx + ((sin α^3 )/α^2 )(2α)−((sin α^2 )/α)(1) = ∫_α ^α^2 cos αx dx + ((2sin α^3 −sin α^2 )/α) = [ (1/α)sin αx ]_α ^α^2 + ((2sin α^3 −sin α^2 )/α) = ((sin α^3 −sin α^2 )/α)+((2sin α^3 −sin α^2 )/α) = ((3sin α^3 −2sin α^2 )/α)](Q139879.png)
Answered by mathmax by abdo last updated on 02/May/21
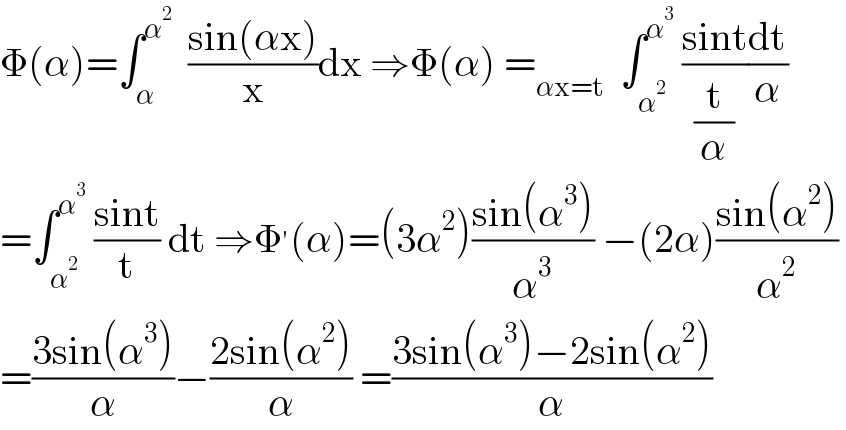
| ||
Question and Answers Forum | ||
Question Number 139878 by bramlexs22 last updated on 02/May/21 | ||
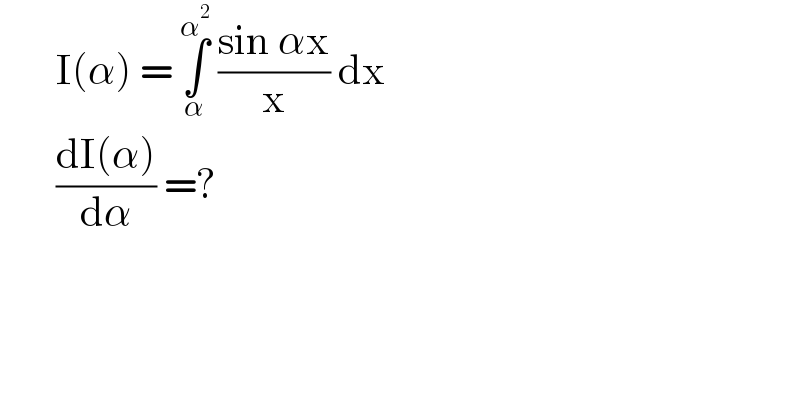 | ||
Answered by EDWIN88 last updated on 02/May/21 | ||
![(dI/dα) = ∫_α ^α^2 (∂/∂α)(((sin αx)/x)) dx + ((sin α^3 )/α^2 )(2α)−((sin α^2 )/α)(1) = ∫_α ^α^2 cos αx dx + ((2sin α^3 −sin α^2 )/α) = [ (1/α)sin αx ]_α ^α^2 + ((2sin α^3 −sin α^2 )/α) = ((sin α^3 −sin α^2 )/α)+((2sin α^3 −sin α^2 )/α) = ((3sin α^3 −2sin α^2 )/α)](Q139879.png) | ||
| ||
Answered by mathmax by abdo last updated on 02/May/21 | ||
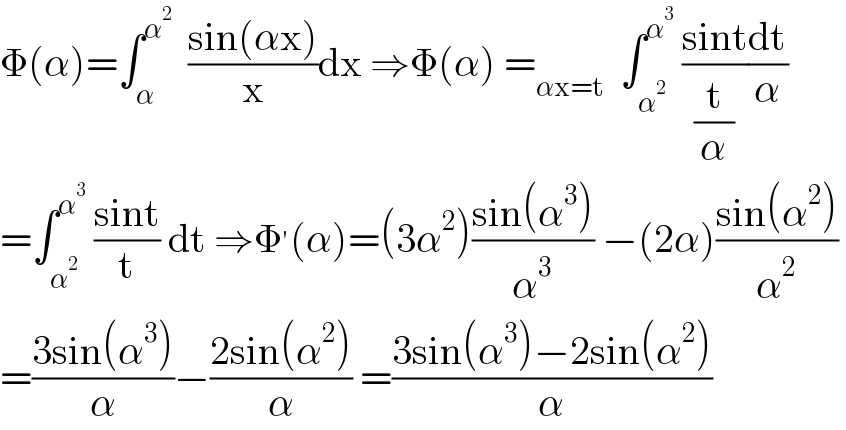 | ||
| ||