Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 139948 by qaz last updated on 02/May/21

$$If{x}^2+xy+y^2=0$$$$find::{\left(\frac{x}{x+y}\right)}^{2023}+{\left(\frac{y}{x+y}\right)}^{2023}$$

Answered by Rasheed.Sindhi last updated on 04/May/21

$$\frac{x}{y}+\frac{y}{x}=-1\Rightarrow \frac{y}{x}=-(1+\frac{x}{y})$$$$\frac{x}{y}=-(1+\frac{y}{x})$$$${\left(\frac{x}{x+y}\right)}^{2023}+{\left(\frac{y}{x+y}\right)}^{2023}$$$$={(1+\frac{y}{x})}^{-2023}+{(1+\frac{x}{y})}^{-2023}$$$$={(1-(1+\frac{x}{y}))}^{-2023}+(1-{(1+\frac{y}{x})}^{-2023}$$$$={(-\frac{x}{y})}^{-2023}+{(-\frac{y}{x})}^{-2023}$$$$={(-\frac{y}{x})}^{2023}+{(-\frac{x}{y})}^{2023}$$$$=-{\left(\frac{y}{x}\right)}^{2023}-{\left(\frac{x}{y}\right)}^{2023}$$$$\mathrm{Continue}$$

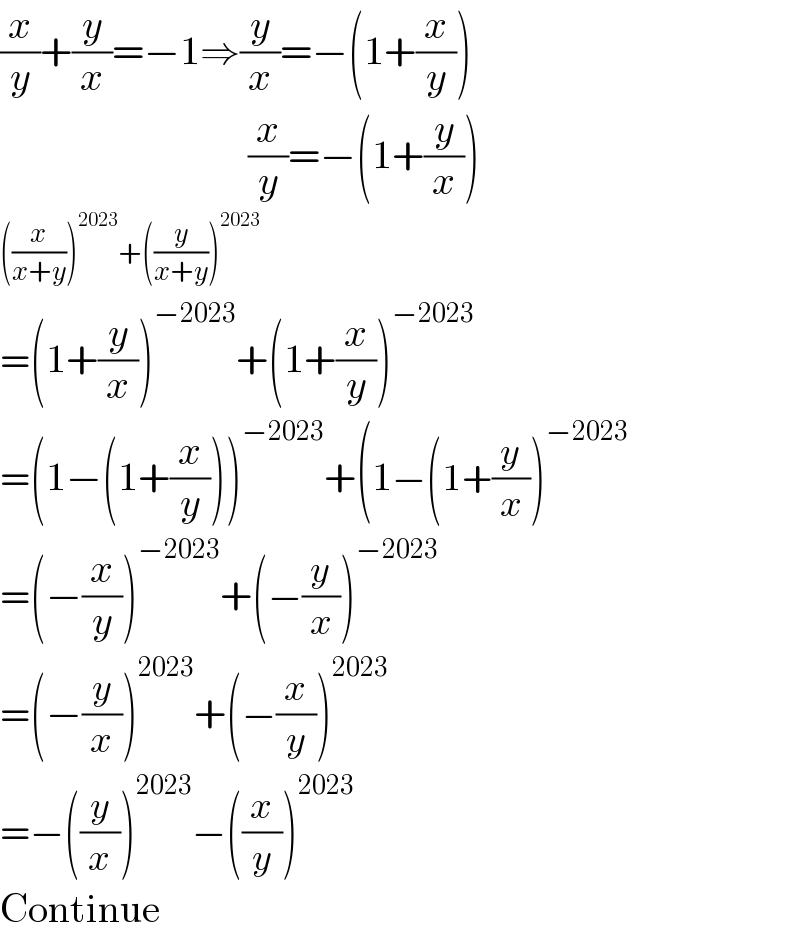
Answered by mathmax by abdo last updated on 02/May/21

$${\mathrm{x}}^2+\mathrm{xy}+{\mathrm{y}}^2=0\mathrm{for}\mathrm{unknown}\mathrm{x}$$$$\mathrm{\Delta }={\mathrm{y}}^2-{4\mathrm{y}}^2=-{3\mathrm{y}}^2\Rightarrow {\mathrm{x}}_1=\frac{-\mathrm{y}+\mathrm{i}\sqrt{3}\mathrm{y}}{2}=\mathrm{y}{\mathrm{e}}^{\frac{\mathrm{i}2\pi }{3}}\mathrm{and}{\mathrm{x}}_2={\mathrm{ye}}^{-\frac{\mathrm{i}2\pi }{3}}$$$$\mathrm{for}\mathrm{x}={\mathrm{x}}_1\mathrm{we}\mathrm{get}\mathrm{\Phi }(\mathrm{x},\mathrm{y})={\left(\frac{\mathrm{x}}{\mathrm{x}+\mathrm{y}}\right)}^{2023}+{\left(\frac{\mathrm{y}}{\mathrm{x}+\mathrm{y}}\right)}^{2023}$$$$={\left(\frac{{\mathrm{ye}}^{\frac{2\mathrm{i}\pi }{3}}}{\mathrm{y}{\mathrm{e}}^{\frac{\mathrm{i}2\pi }{3}}+\mathrm{y}}\right)}^{2023}+{\left(\frac{\mathrm{y}}{{\mathrm{ye}}^{\frac{\mathrm{i}2\pi }{3}}+\mathrm{y}}\right)}^{2023}={\left(\frac{{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}{1+{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}\right)}^{2023}+{\left(\frac{1}{1+{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}\right)}^{2023}$$$$=\frac{{\left({\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}\right)}^{2023}+1}{{(1+{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}})}^{2023}}\mathrm{we}\mathrm{have}1+\mathrm{j}+{\mathrm{j}}^2=0\Rightarrow 1+\mathrm{j}=-{\mathrm{j}}^2\Rightarrow {(1+\mathrm{j})}^{2023}=-{\mathrm{j}}^{4046}$$$$\Rightarrow \mathrm{\Phi }(\mathrm{x},\mathrm{y})=-\frac{1+{\mathrm{e}}^{\frac{4046\mathrm{i}\pi }{3}}}{{\left({\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}\right)}^{4046}}=-\frac{1+{\mathrm{e}}^{\frac{4046\mathrm{i}\pi }{3}}}{{\mathrm{e}}^{\frac{8092\mathrm{i}\pi }{3}}}$$$$=-{\mathrm{e}}^{\frac{8092\mathrm{i}\pi }{3}}(1+{\mathrm{e}}^{\frac{4046\mathrm{i}\pi }{3}})\mathrm{rest}\mathrm{simplification}\mathrm{of}\mathrm{\Phi }(\mathrm{x},\mathrm{y})....$$

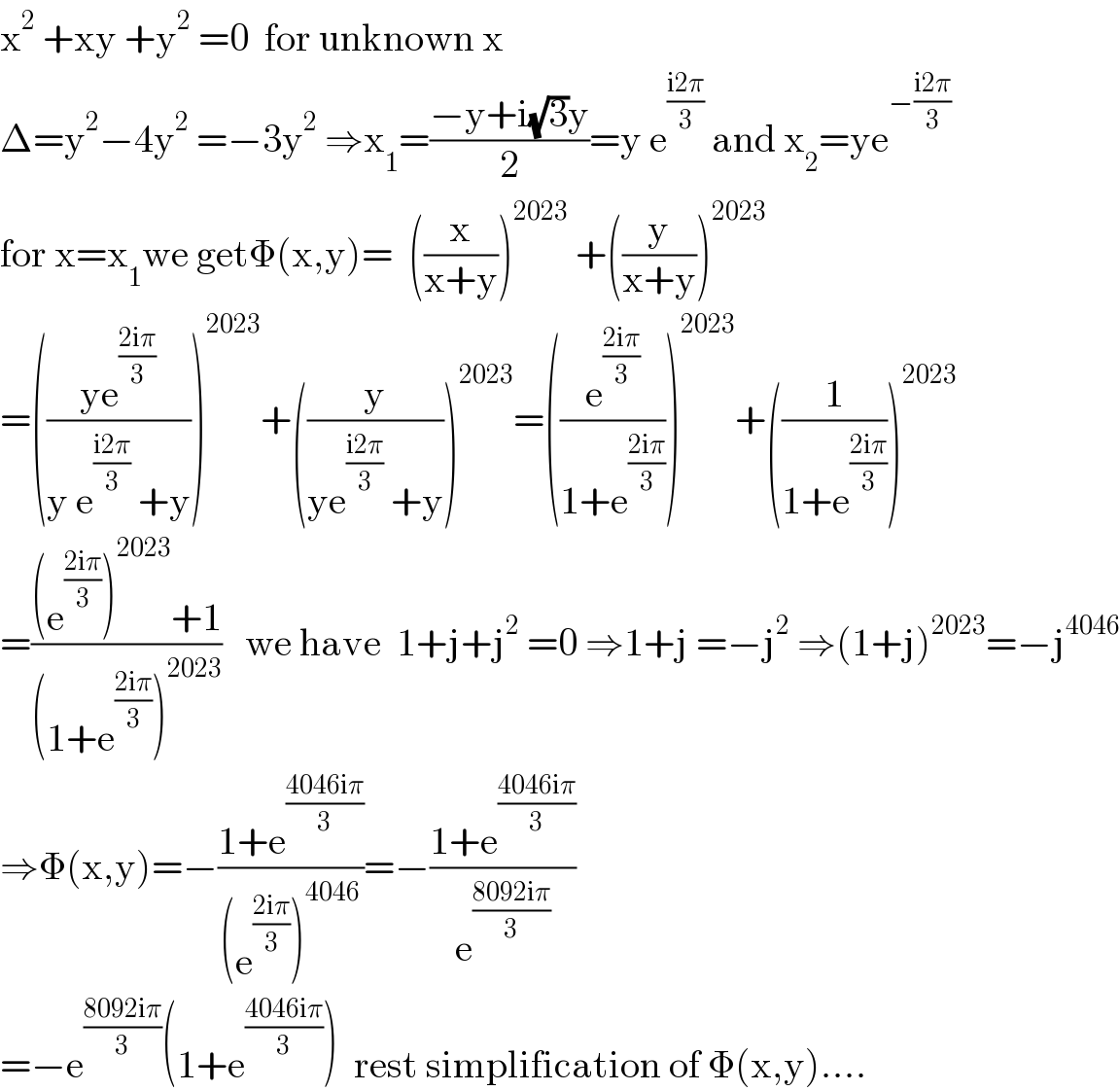
Answered by mr W last updated on 02/May/21

$$lett=\frac{y}{x}$$$$x^2+{tx}^2+t^2{x}^2=0$$$$t^2+t+1=0\Rightarrow t+1=-t^2$$$$\frac{1}{t^2}+\frac{1}{t}+1=0$$$$\frac{1}{t}\ne 1$$$$(\frac{1}{t^2}+\frac{1}{t}+1)(\frac{1}{t}-1)=0$$$${\left(\frac{1}{t}\right)}^3-1=0$$$$\Rightarrow {\left(\frac{1}{t}\right)}^3=1$$$$$$$${\left(\frac{x}{x+y}\right)}^{2023}+{\left(\frac{y}{x+y}\right)}^{2023}$$$$={\left(\frac{1}{1+t}\right)}^{2023}+{\left(\frac{t}{1+t}\right)}^{2023}$$$$={(-\frac{1}{t^2})}^{2023}+{(-\frac{1}{t})}^{2023}$$$$=-{\left(\frac{1}{t^2}\right)}^{2023}-{\left(\frac{1}{t}\right)}^{2023}$$$$=-{\left(\frac{1}{t}\right)}^{3\times 1348}{\left(\frac{1}{t}\right)}^2-{\left(\frac{1}{t}\right)}^{3\times 674}\left(\frac{1}{t}\right)$$$$=-{\left(\frac{1}{t}\right)}^2-\left(\frac{1}{t}\right)$$$$=-[{\left(\frac{1}{t}\right)}^2+\left(\frac{1}{t}\right)+1]+1$$$$=-0+1$$$$=1$$

Commented by qaz last updated on 04/May/21

$$thankyouSirs.mr{W}^{\prime }swayiscorrect.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com