Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 139973 by ajfour last updated on 02/May/21

Commented by ajfour last updated on 02/May/21

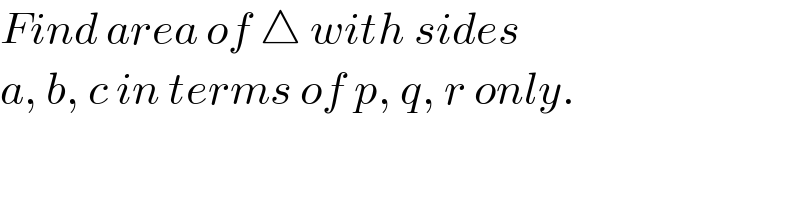
Find area of △ with sides a, b, c in terms of p, q, r only.

$${Find}\:{area}\:{of}\:\bigtriangleup\:{with}\:{sides}\: \\ $$$${a},\:{b},\:{c}\:{in}\:{terms}\:{of}\:{p},\:{q},\:{r}\:{only}. \\ $$

Answered by ajfour last updated on 02/May/21

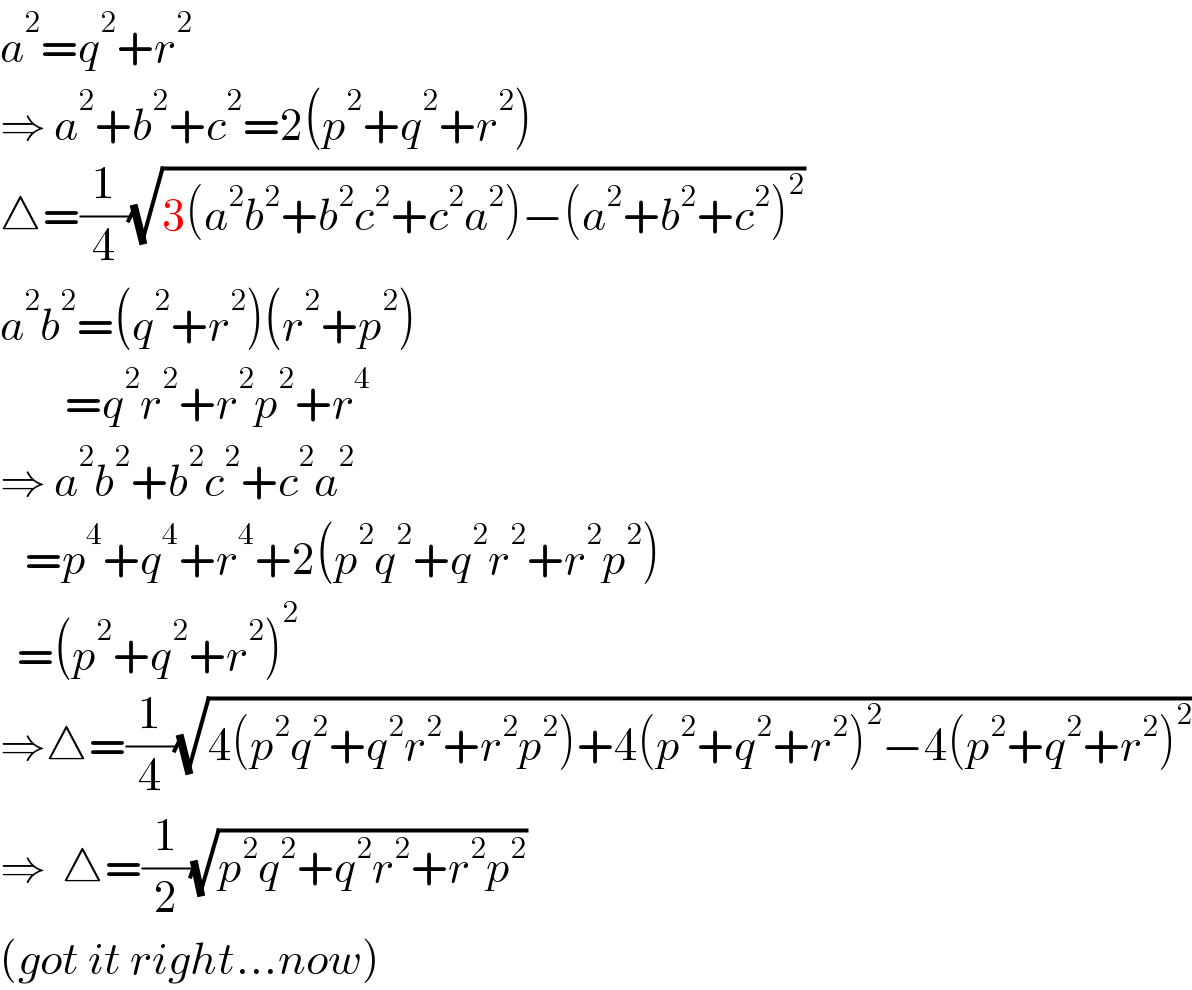
a^2 =q^2 +r^2 ⇒ a^2 +b^2 +c^2 =2(p^2 +q^2 +r^2 ) △=(1/4)(√(3(a^2 b^2 +b^2 c^2 +c^2 a^2 )−(a^2 +b^2 +c^2 )^2 )) a^2 b^2 =(q^2 +r^2 )(r^2 +p^2 ) =q^2 r^2 +r^2 p^2 +r^4 ⇒ a^2 b^2 +b^2 c^2 +c^2 a^2 =p^4 +q^4 +r^4 +2(p^2 q^2 +q^2 r^2 +r^2 p^2 ) =(p^2 +q^2 +r^2 )^2 ⇒△=(1/4)(√(4(p^2 q^2 +q^2 r^2 +r^2 p^2 )+4(p^2 +q^2 +r^2 )^2 −4(p^2 +q^2 +r^2 )^2 )) ⇒ △=(1/2)(√(p^2 q^2 +q^2 r^2 +r^2 p^2 )) (got it right...now)

$${a}^{\mathrm{2}} ={q}^{\mathrm{2}} +{r}^{\mathrm{2}} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right) \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{3}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} =\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} +{p}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:={q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} +{r}^{\mathrm{4}} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \\ $$$$\:\:\:={p}^{\mathrm{4}} +{q}^{\mathrm{4}} +{r}^{\mathrm{4}} +\mathrm{2}\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} \right) \\ $$$$\:\:=\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\bigtriangleup=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{4}\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} \right)+\mathrm{4}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\bigtriangleup=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} } \\ $$$$\left({got}\:{it}\:{right}...{now}\right) \\ $$

Commented by ajfour last updated on 02/May/21

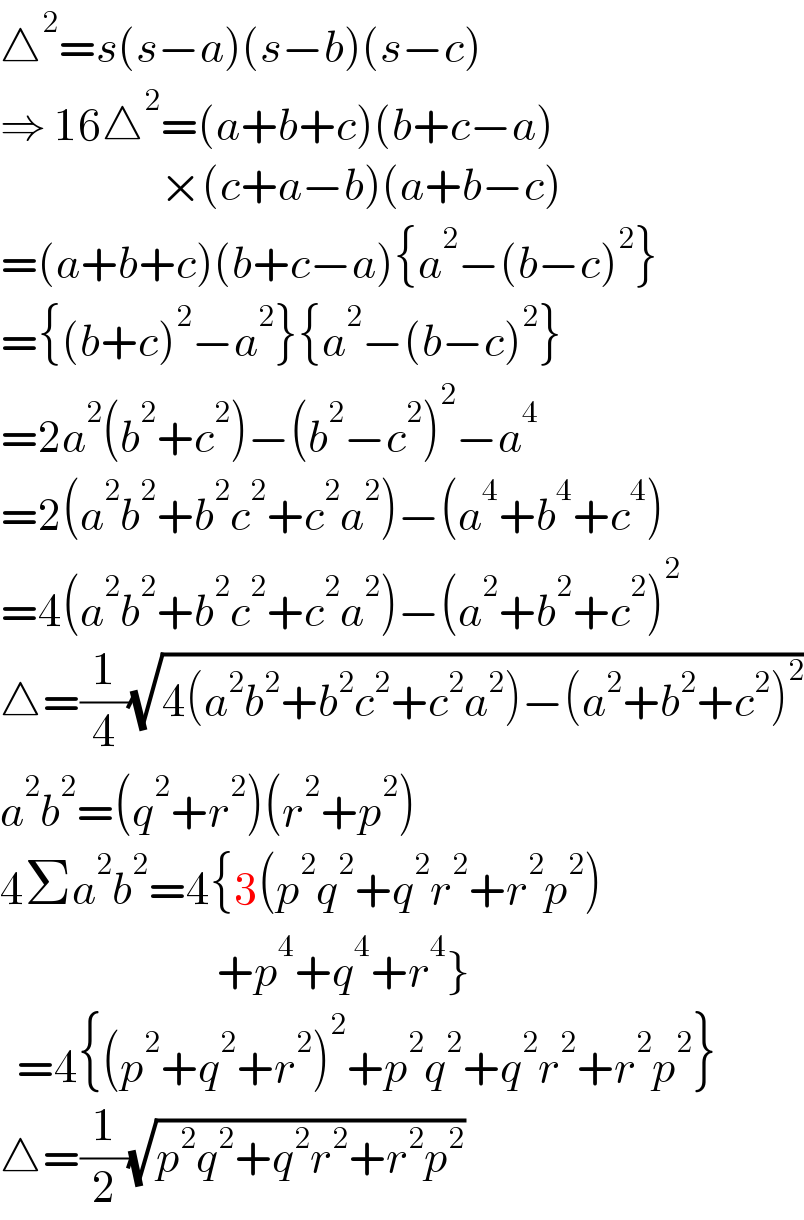
△^2 =s(s−a)(s−b)(s−c) ⇒ 16△^2 =(a+b+c)(b+c−a) ×(c+a−b)(a+b−c) =(a+b+c)(b+c−a){a^2 −(b−c)^2 } ={(b+c)^2 −a^2 }{a^2 −(b−c)^2 } =2a^2 (b^2 +c^2 )−(b^2 −c^2 )^2 −a^4 =2(a^2 b^2 +b^2 c^2 +c^2 a^2 )−(a^4 +b^4 +c^4 ) =4(a^2 b^2 +b^2 c^2 +c^2 a^2 )−(a^2 +b^2 +c^2 )^2 △=(1/4)(√(4(a^2 b^2 +b^2 c^2 +c^2 a^2 )−(a^2 +b^2 +c^2 )^2 )) a^2 b^2 =(q^2 +r^2 )(r^2 +p^2 ) 4Σa^2 b^2 =4{3(p^2 q^2 +q^2 r^2 +r^2 p^2 ) +p^4 +q^4 +r^4 } =4{(p^2 +q^2 +r^2 )^2 +p^2 q^2 +q^2 r^2 +r^2 p^2 } △=(1/2)(√(p^2 q^2 +q^2 r^2 +r^2 p^2 ))

$$\bigtriangleup^{\mathrm{2}} ={s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right) \\ $$$$\Rightarrow\:\mathrm{16}\bigtriangleup^{\mathrm{2}} =\left({a}+{b}+{c}\right)\left({b}+{c}−{a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\left({c}+{a}−{b}\right)\left({a}+{b}−{c}\right) \\ $$$$=\left({a}+{b}+{c}\right)\left({b}+{c}−{a}\right)\left\{{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} \right\} \\ $$$$=\left\{\left({b}+{c}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right\}\left\{{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} \right\} \\ $$$$=\mathrm{2}{a}^{\mathrm{2}} \left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)^{\mathrm{2}} −{a}^{\mathrm{4}} \\ $$$$=\mathrm{2}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right) \\ $$$$=\mathrm{4}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{4}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} =\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} +{p}^{\mathrm{2}} \right) \\ $$$$\mathrm{4}\Sigma{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{4}\left\{\mathrm{3}\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} \right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{p}^{\mathrm{4}} +{q}^{\mathrm{4}} +{r}^{\mathrm{4}} \right\} \\ $$$$\:\:=\mathrm{4}\left\{\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{2}} +{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} \right\} \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} } \\ $$

Answered by mr W last updated on 02/May/21

Commented by mr W last updated on 02/May/21

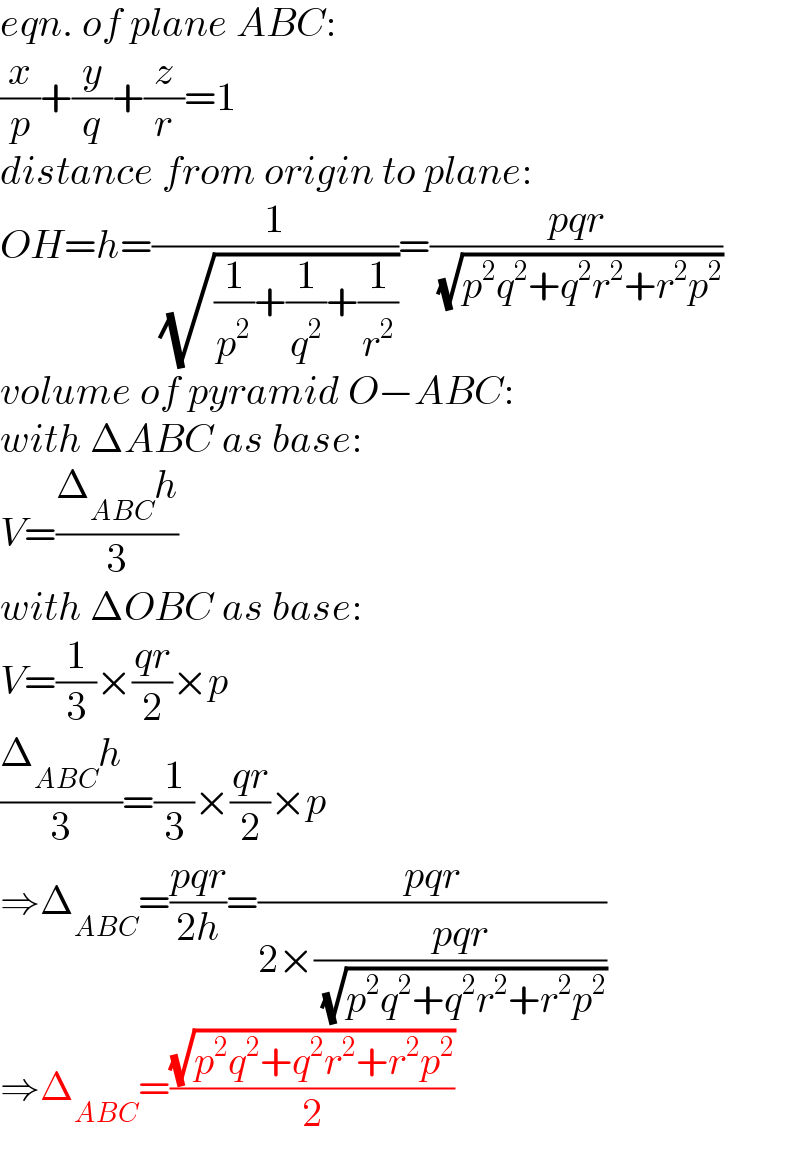
eqn. of plane ABC: (x/p)+(y/q)+(z/r)=1 distance from origin to plane: OH=h=(1/( (√((1/p^2 )+(1/q^2 )+(1/r^2 )))))=((pqr)/( (√(p^2 q^2 +q^2 r^2 +r^2 p^2 )))) volume of pyramid O−ABC: with ΔABC as base: V=((Δ_(ABC) h)/3) with ΔOBC as base: V=(1/3)×((qr)/2)×p ((Δ_(ABC) h)/3)=(1/3)×((qr)/2)×p ⇒Δ_(ABC) =((pqr)/(2h))=((pqr)/(2×((pqr)/( (√(p^2 q^2 +q^2 r^2 +r^2 p^2 )))))) ⇒Δ_(ABC) =((√(p^2 q^2 +q^2 r^2 +r^2 p^2 ))/2)

$${eqn}.\:{of}\:{plane}\:{ABC}: \\ $$$$\frac{{x}}{{p}}+\frac{{y}}{{q}}+\frac{{z}}{{r}}=\mathrm{1} \\ $$$${distance}\:{from}\:{origin}\:{to}\:{plane}: \\ $$$${OH}={h}=\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }}}=\frac{{pqr}}{\:\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} }} \\ $$$${volume}\:{of}\:{pyramid}\:{O}−{ABC}: \\ $$$${with}\:\Delta{ABC}\:{as}\:{base}: \\ $$$${V}=\frac{\Delta_{{ABC}} {h}}{\mathrm{3}} \\ $$$${with}\:\Delta{OBC}\:{as}\:{base}: \\ $$$${V}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{{qr}}{\mathrm{2}}×{p} \\ $$$$\frac{\Delta_{{ABC}} {h}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{{qr}}{\mathrm{2}}×{p} \\ $$$$\Rightarrow\Delta_{{ABC}} =\frac{{pqr}}{\mathrm{2}{h}}=\frac{{pqr}}{\mathrm{2}×\frac{{pqr}}{\:\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} }}} \\ $$$$\Rightarrow\Delta_{{ABC}} =\frac{\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} }}{\mathrm{2}} \\ $$

Commented by ajfour last updated on 02/May/21

Thanks Sir!

Commented by ajfour last updated on 21/May/21

what's the expression for circumradius of ∆ABC in terms of p, q, r Sir ?

Answered by ajfour last updated on 02/May/21

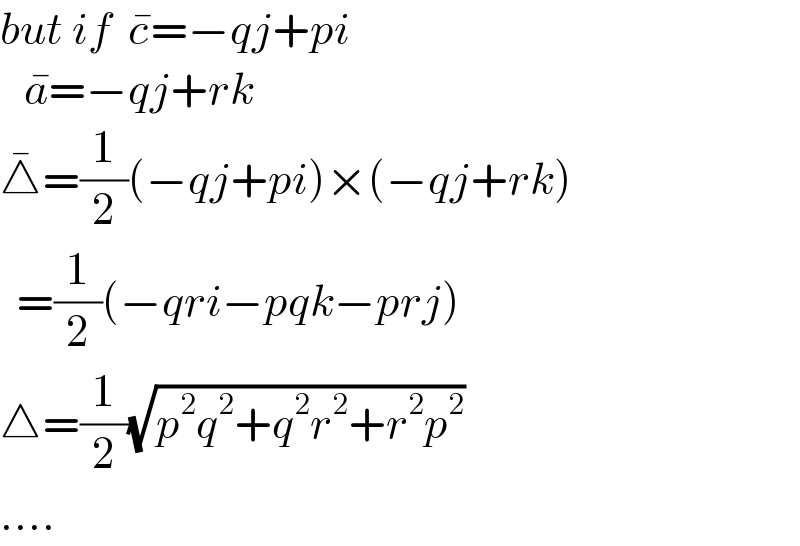
but if c^� =−qj+pi a^� =−qj+rk △^� =(1/2)(−qj+pi)×(−qj+rk) =(1/2)(−qri−pqk−prj) △=(1/2)(√(p^2 q^2 +q^2 r^2 +r^2 p^2 )) ....

$${but}\:{if}\:\:\bar {{c}}=−{qj}+{pi} \\ $$$$\:\:\:\bar {{a}}=−{qj}+{rk} \\ $$$$\bar {\bigtriangleup}=\frac{\mathrm{1}}{\mathrm{2}}\left(−{qj}+{pi}\right)×\left(−{qj}+{rk}\right) \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(−{qri}−{pqk}−{prj}\right) \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} } \\ $$$$.... \\ $$

Commented by mr W last updated on 02/May/21

vector way is best!

$${vector}\:{way}\:{is}\:{best}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com