Question Number 14014 by tawa tawa last updated on 26/May/17
$$\int\mathrm{cos}^{\mathrm{n}} \left(\mathrm{x}\right)\:\:\mathrm{dx} \\ $$$$\mathrm{please}\:\mathrm{i}\:\mathrm{need}\:\mathrm{workings}. \\ $$
Answered by mrW1 last updated on 26/May/17
![I_n =∫cos^n (x) dx=∫cos^(n−1) (x) dsin (x) using ∫udv=uv−∫vdu =sin (x) cos^(n−1) (x)+(n−1)∫sin^2 (x) cos^(n−2) (x)dx =sin (x) cos^(n−1) (x)+(n−1)∫[1−cos^2 (x)] cos^(n−2) (x)dx =sin (x) cos^(n−1) (x)+(n−1)∫cos^(n−2) (x) dx−(n−1)∫cos^n (x) dx ⇒I_n =sin (x) cos^(n−1) (x)+(n−1)∫cos^(n−2) (x) dx−(n−1)I_n ⇒nI_n =sin (x) cos^(n−1) (x)+(n−1)I_(n−2) ⇒I_n =(1/n)sin (x) cos^(n−1) (x)+((n−1)/n)I_(n−2) ⇒I_(n−2) =(1/(n−2))sin (x) cos^(n−3) (x)+((n−3)/(n−2))I_(n−4) ...... if n=even .... ⇒I_2 =(1/2)sin (x) cos (x)+(1/2)I_0 ⇒I_0 =∫dx=x+C ...... if n=odd .... ⇒I_3 =(1/3)sin (x) cos^2 (x)+(2/3)I_1 ⇒I_1 =∫cos (x) dx=sin (x)+C](Q14017.png)
$${I}_{{n}} =\int\mathrm{cos}^{\mathrm{n}} \left(\mathrm{x}\right)\:\:\mathrm{dx}=\int\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)\:{d}\mathrm{sin}\:\left({x}\right) \\ $$$${using}\:\int{udv}={uv}−\int{vdu} \\ $$$$=\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\left({n}−\mathrm{1}\right)\int\mathrm{sin}^{\mathrm{2}} \:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{2}} \:\left({x}\right){dx} \\ $$$$=\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\left({n}−\mathrm{1}\right)\int\left[\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\left({x}\right)\right]\:\mathrm{cos}^{{n}−\mathrm{2}} \:\left({x}\right){dx} \\ $$$$=\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\left({n}−\mathrm{1}\right)\int\mathrm{cos}^{{n}−\mathrm{2}} \:\left({x}\right)\:{dx}−\left({n}−\mathrm{1}\right)\int\mathrm{cos}^{{n}} \:\left({x}\right)\:{dx} \\ $$$$\Rightarrow{I}_{{n}} =\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\left({n}−\mathrm{1}\right)\int\mathrm{cos}^{{n}−\mathrm{2}} \:\left({x}\right)\:{dx}−\left({n}−\mathrm{1}\right){I}_{{n}} \\ $$$$\Rightarrow{nI}_{{n}} =\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\left({n}−\mathrm{1}\right){I}_{{n}−\mathrm{2}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{1}}{{n}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right)+\frac{{n}−\mathrm{1}}{{n}}{I}_{{n}−\mathrm{2}} \\ $$$$\Rightarrow{I}_{{n}−\mathrm{2}} =\frac{\mathrm{1}}{{n}−\mathrm{2}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{3}} \:\left({x}\right)+\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}{I}_{{n}−\mathrm{4}} \\ $$$$......\:{if}\:{n}={even}\:.... \\ $$$$\Rightarrow{I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}\:\left({x}\right)+\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{0}} \\ $$$$\Rightarrow{I}_{\mathrm{0}} =\int{dx}={x}+{C} \\ $$$$ \\ $$$$......\:{if}\:{n}={odd}\:.... \\ $$$$\Rightarrow{I}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{\mathrm{2}} \:\left({x}\right)+\frac{\mathrm{2}}{\mathrm{3}}{I}_{\mathrm{1}} \\ $$$$\Rightarrow{I}_{\mathrm{1}} =\int\mathrm{cos}\:\left({x}\right)\:{dx}=\mathrm{sin}\:\left({x}\right)+{C} \\ $$
Commented by tawa tawa last updated on 26/May/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mrW1 last updated on 27/May/17
$${If}\:{n}\:{is}\:{even}\:{we}\:{get}: \\ $$$${I}_{{n}} =\int\mathrm{cos}^{{n}} \:\left({x}\right)\:{dx} \\ $$$$=\frac{\mathrm{1}}{{n}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{\mathrm{1}}{{n}−\mathrm{2}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{3}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{\mathrm{1}}{{n}−\mathrm{4}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{5}} \:\left({x}\right) \\ $$$$+...... \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{{n}−\mathrm{5}}{{n}−\mathrm{4}}\centerdot\centerdot\centerdot\frac{\mathrm{5}}{\mathrm{6}}\centerdot\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{\mathrm{3}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{{n}−\mathrm{5}}{{n}−\mathrm{4}}\centerdot\centerdot\centerdot\frac{\mathrm{5}}{\mathrm{6}}\centerdot\frac{\mathrm{3}}{\mathrm{4}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}\:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{{n}−\mathrm{5}}{{n}−\mathrm{4}}\centerdot\centerdot\centerdot\frac{\mathrm{5}}{\mathrm{6}}\centerdot\frac{\mathrm{3}}{\mathrm{4}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}{x}+{C} \\ $$$$=\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\frac{\boldsymbol{{n}}}{\mathrm{2}}} {\boldsymbol{\sum}}}\frac{\overset{=\mathrm{1}\:{if}\:{k}=\mathrm{1}} {\left(\boldsymbol{{n}}−\mathrm{1}\right)\left(\boldsymbol{{n}}−\mathrm{3}\right)\centerdot\centerdot\centerdot\left(\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{3}\right)}}{\boldsymbol{{n}}\left(\boldsymbol{{n}}−\mathrm{2}\right)\centerdot\centerdot\centerdot\left(\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{2}\right)}\centerdot\:\boldsymbol{\mathrm{sin}}\:\left(\boldsymbol{{x}}\right)\:\boldsymbol{\mathrm{cos}}^{\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{1}} \:\left(\boldsymbol{{x}}\right) \\ $$$$+\frac{\left(\boldsymbol{{n}}−\mathrm{1}\right)!!}{\boldsymbol{{n}}!!}\boldsymbol{{x}}+\boldsymbol{{C}} \\ $$$$ \\ $$$${if}\:{n}\:{is}\:{odd}\:{we}\:{get}: \\ $$$${I}_{{n}} =\int\mathrm{cos}^{{n}} \:\left({x}\right)\:{dx} \\ $$$$=\frac{\mathrm{1}}{{n}}\:\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{1}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{\mathrm{1}}{{n}−\mathrm{2}}\:\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{3}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{\mathrm{1}}{{n}−\mathrm{4}}\:\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{{n}−\mathrm{5}} \:\left({x}\right) \\ $$$$+...... \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{{n}−\mathrm{5}}{{n}−\mathrm{4}}\centerdot\centerdot\centerdot\frac{\mathrm{4}}{\mathrm{5}}\centerdot\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{\mathrm{2}} \:\left({x}\right) \\ $$$$+\frac{{n}−\mathrm{1}}{{n}}\centerdot\frac{{n}−\mathrm{3}}{{n}−\mathrm{2}}\centerdot\frac{{n}−\mathrm{5}}{{n}−\mathrm{4}}\centerdot\centerdot\centerdot\frac{\mathrm{4}}{\mathrm{5}}\centerdot\frac{\mathrm{2}}{\mathrm{3}}\centerdot\frac{\mathrm{1}}{\mathrm{1}}\:\mathrm{sin}\:\left({x}\right)\:\mathrm{cos}^{\mathrm{0}} \:\left({x}\right)+{C} \\ $$$$=\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\frac{\boldsymbol{{n}}+\mathrm{1}}{\mathrm{2}}} {\boldsymbol{\sum}}}\frac{\overset{=\mathrm{1}\:{if}\:{k}=\mathrm{1}} {\left(\boldsymbol{{n}}−\mathrm{1}\right)\left(\boldsymbol{{n}}−\mathrm{3}\right)\centerdot\centerdot\centerdot\left(\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{1}\right)}}{\boldsymbol{{n}}\left(\boldsymbol{{n}}−\mathrm{2}\right)\centerdot\centerdot\centerdot\left(\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{2}\right)}\centerdot\:\boldsymbol{\mathrm{sin}}\:\left(\boldsymbol{{x}}\right)\:\boldsymbol{\mathrm{cos}}^{\boldsymbol{{n}}−\mathrm{2}\boldsymbol{{k}}+\mathrm{1}} \:\left(\boldsymbol{{x}}\right)+\boldsymbol{{C}} \\ $$
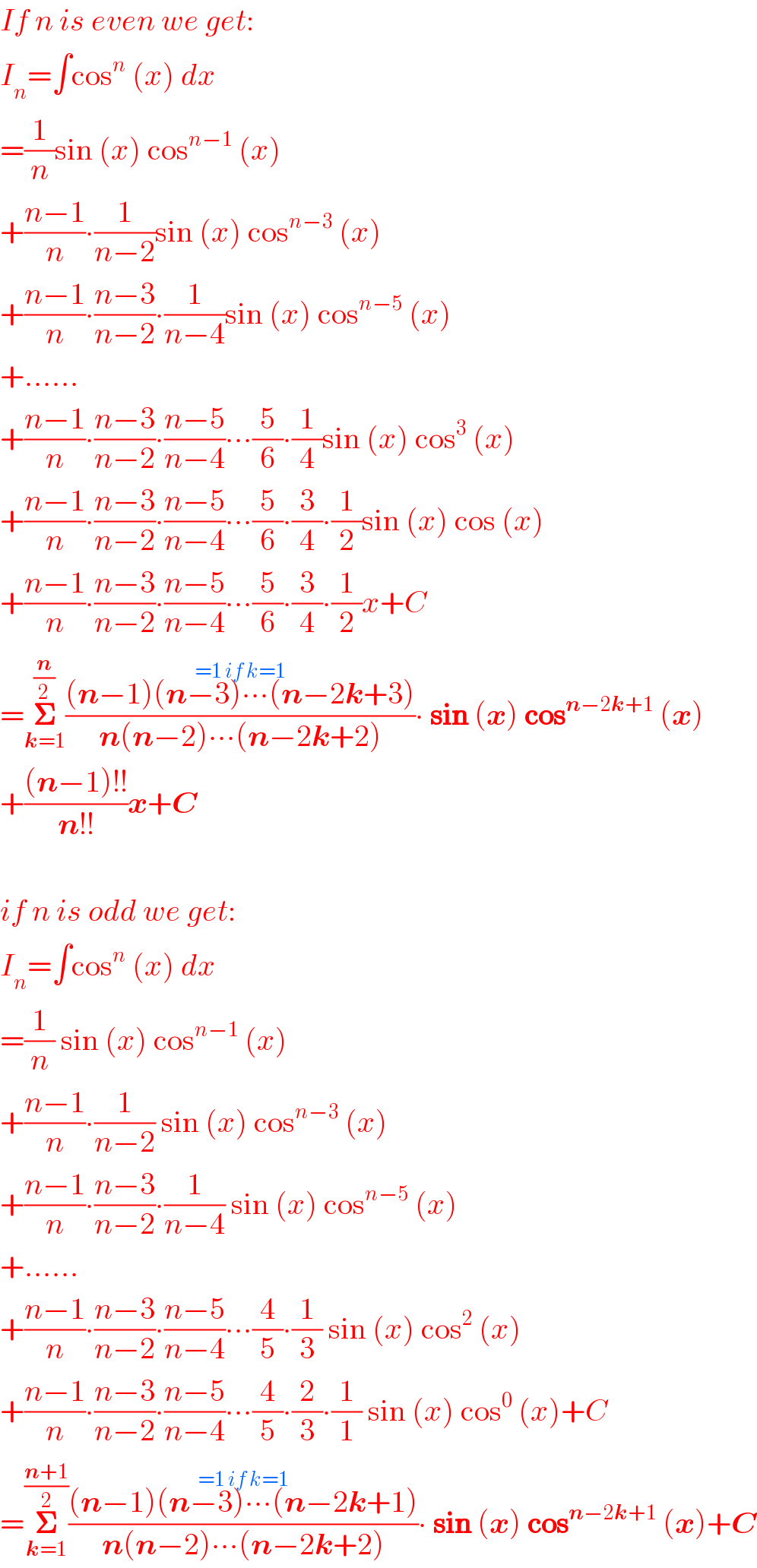
Commented by tawa tawa last updated on 27/May/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 27/May/17
$${I}_{{n}} =\int{cos}^{\mathrm{2}} {x}.{cos}^{{n}−\mathrm{2}} {xdx}= \\ $$$$=\int{cos}^{{n}−\mathrm{2}} {xdx}−\int{sin}^{\mathrm{2}} {x}.{cos}^{{n}−\mathrm{2}} {xdx}= \\ $$$$={I}_{{n}−\mathrm{2}} −\left[\frac{−\mathrm{1}}{{n}−\mathrm{1}}{sinx}.{cos}^{{n}−\mathrm{1}} {x}+\frac{\mathrm{1}}{{n}−\mathrm{1}}\int{cosx}.{cos}^{{n}−\mathrm{1}} {xdx}=\right. \\ $$$$={I}_{{n}−\mathrm{2}} +\frac{\mathrm{1}}{{n}−\mathrm{1}}{sinx}.{cos}^{{n}−\mathrm{1}} {x}−\frac{\mathrm{1}}{{n}−\mathrm{1}}{I}_{{n}} +\boldsymbol{{C}}. \\ $$$$\Rightarrow{I}_{{n}} +\frac{\mathrm{1}}{{n}−\mathrm{1}}{I}_{{n}} ={I}_{{n}−\mathrm{2}} +\frac{\mathrm{1}}{{n}−\mathrm{1}}{sinx}.{cos}^{{n}−\mathrm{1}} {x}+\boldsymbol{{C}}\:\Rightarrow \\ $$$$\frac{{n}}{{n}−\mathrm{1}}{I}_{{n}} ={I}_{{n}−\mathrm{2}} +\frac{\mathrm{1}}{{n}−\mathrm{1}}{sinx}.{cos}^{{n}−\mathrm{1}} {x}+{C} \\ $$$$\Rightarrow{I}_{{n}} =\frac{{n}−\mathrm{1}}{{n}}.{I}_{{n}−\mathrm{2}} +\frac{\mathrm{1}}{{n}}{sinx}.{cos}^{{n}−\mathrm{1}} {x}+{C}. \\ $$$$\left.\mathrm{0}\right){I}_{\mathrm{0}} =\int{dx}={x}+{C}. \\ $$$$\left.\mathrm{1}\right){I}_{\mathrm{1}} =\int{cosxdx}={sinx}+\boldsymbol{{C}} \\ $$$$\left.\mathrm{2}\right){I}_{\mathrm{2}} =\int{cos}^{\mathrm{2}} {xdx}=\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\mathrm{1}}{\mathrm{4}}{sin}\mathrm{2}{x}+\boldsymbol{{C}} \\ $$$$\left.\mathrm{3}\right){n}>\mathrm{2}\Rightarrow{formula}\:{given}\:{above}. \\ $$$${example}:{I}_{\mathrm{3}} \\ $$$${I}_{\mathrm{3}} =\int{cos}^{\mathrm{3}} {xdx}=\int{cosx}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right){dx}= \\ $$$$={sinx}−\frac{\mathrm{1}}{\mathrm{3}}{sin}^{\mathrm{3}} {x}+\boldsymbol{{C}} \\ $$$${I}_{\mathrm{3}} =\frac{\mathrm{3}−\mathrm{1}}{\mathrm{3}}{I}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{3}}{sinx}.{cos}^{\mathrm{2}} {x}=\frac{\mathrm{2}}{\mathrm{3}}{I}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{3}}{sinx}.{cos}^{\mathrm{2}} {x}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}{sinx}+\frac{\mathrm{1}}{\mathrm{3}}{sinx}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)={sinx}−\frac{\mathrm{1}}{\mathrm{3}}{sin}^{\mathrm{3}} {x}+{C} \\ $$
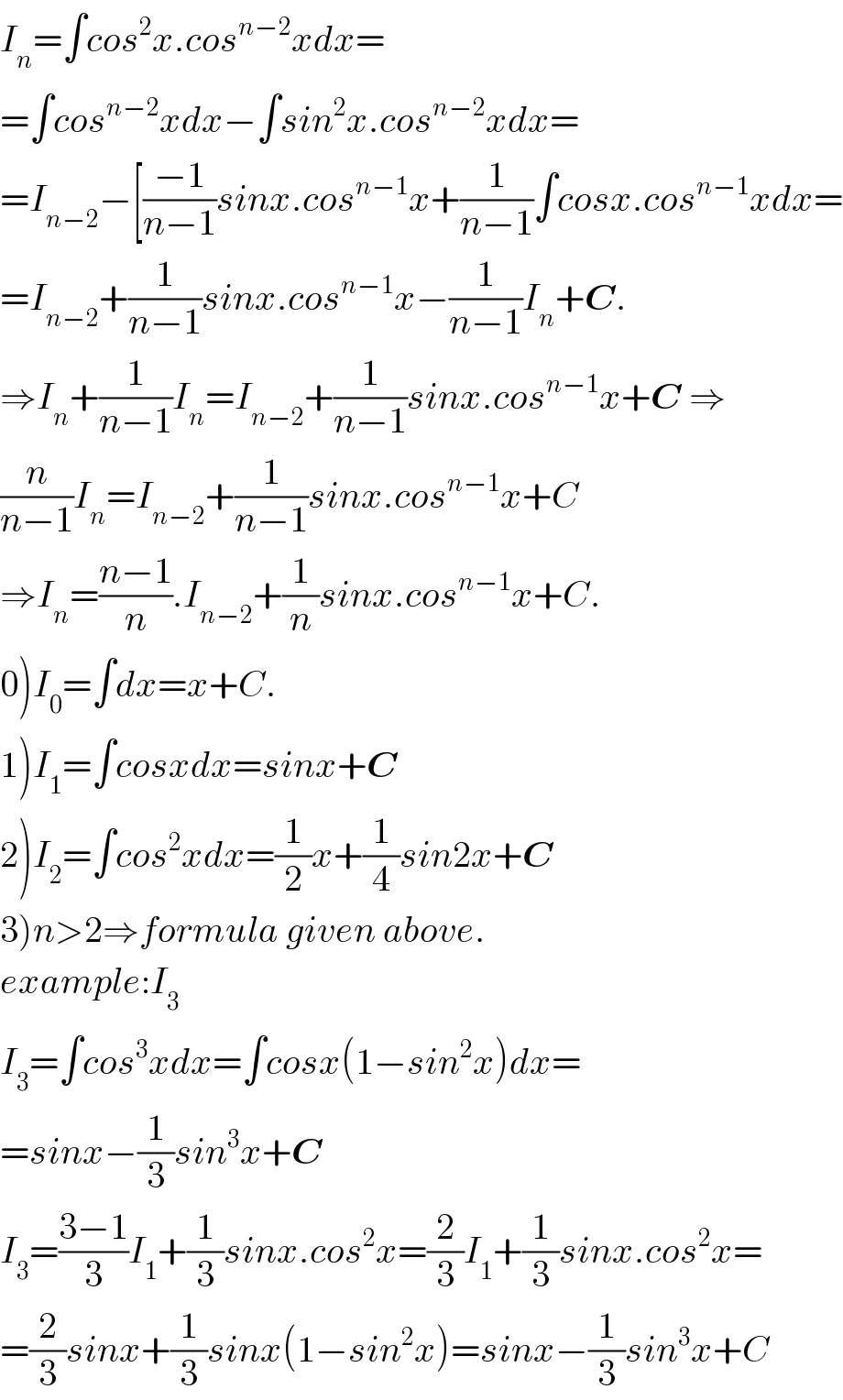
Commented by tawa tawa last updated on 27/May/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$