Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 14078 by Tinkutara last updated on 27/May/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 27/May/17

4cos^3 x−3cosx−(√3)sinx.cosx+cos^2 x−(1/2)=−2 8cos^3 x+2cos^2 x−2(√3)sinx.cosx−6cosx+3=0 cosx=t⇒ 8t^3 +2t^2 −6t+3=2(√3)t(√(1−t^2 )) 64t^6 +4t^4 +36t^2 +9+32t^5 −96t^4 +48t^3 −24t^3 +12t^2 −36t=12t^2 −12t^4 ⇒64t^6 +32t^5 −80t^4 +24t^3 +36t^2 −36t+9=0 ⇒t=cosx=(1/2)⇒x=2kπ±(π/3) .■

$$\mathrm{4}{cos}^{\mathrm{3}} {x}−\mathrm{3}{cosx}−\sqrt{\mathrm{3}}{sinx}.{cosx}+{cos}^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{2}}=−\mathrm{2} \\ $$$$\mathrm{8}{cos}^{\mathrm{3}} {x}+\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{2}\sqrt{\mathrm{3}}{sinx}.{cosx}−\mathrm{6}{cosx}+\mathrm{3}=\mathrm{0} \\ $$$${cosx}={t}\Rightarrow \\ $$$$\mathrm{8}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{6}{t}+\mathrm{3}=\mathrm{2}\sqrt{\mathrm{3}}{t}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\mathrm{64}{t}^{\mathrm{6}} +\mathrm{4}{t}^{\mathrm{4}} +\mathrm{36}{t}^{\mathrm{2}} +\mathrm{9}+\mathrm{32}{t}^{\mathrm{5}} −\mathrm{96}{t}^{\mathrm{4}} +\mathrm{48}{t}^{\mathrm{3}} −\mathrm{24}{t}^{\mathrm{3}} +\mathrm{12}{t}^{\mathrm{2}} −\mathrm{36}{t}=\mathrm{12}{t}^{\mathrm{2}} −\mathrm{12}{t}^{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{64}{t}^{\mathrm{6}} +\mathrm{32}{t}^{\mathrm{5}} −\mathrm{80}{t}^{\mathrm{4}} +\mathrm{24}{t}^{\mathrm{3}} +\mathrm{36}{t}^{\mathrm{2}} −\mathrm{36}{t}+\mathrm{9}=\mathrm{0} \\ $$$$\Rightarrow{t}={cosx}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{x}=\mathrm{2}{k}\pi\pm\frac{\pi}{\mathrm{3}}\:\:.\blacksquare \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 27/May/17

Commented by ajfour last updated on 28/May/17

• sin [2(2kπ−(π/3))−((7π)/6)] =sin (4kπ−((11π)/6))=sin (π/6)≠−1 . • sin [2(2kπ+(π/3))−((7π)/6)] =sin (4kπ−(π/2))=−1.

$$\bullet\:\:\:\mathrm{sin}\:\left[\mathrm{2}\left(\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{3}}\right)−\frac{\mathrm{7}\pi}{\mathrm{6}}\right] \\ $$$$\:\:\:\:\:\:=\mathrm{sin}\:\left(\mathrm{4}{k}\pi−\frac{\mathrm{11}\pi}{\mathrm{6}}\right)=\mathrm{sin}\:\frac{\pi}{\mathrm{6}}\neq−\mathrm{1}\:. \\ $$$$\bullet\:\:\:\:\mathrm{sin}\:\left[\mathrm{2}\left(\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{3}}\right)−\frac{\mathrm{7}\pi}{\mathrm{6}}\right] \\ $$$$\:\:\:\:\:\:\:=\mathrm{sin}\:\left(\mathrm{4}{k}\pi−\frac{\pi}{\mathrm{2}}\right)=−\mathrm{1}. \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 28/May/17

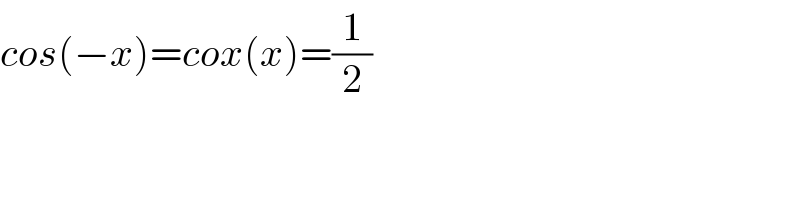
cos(−x)=cox(x)=(1/2)

$${cos}\left(−{x}\right)={cox}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Answered by ajfour last updated on 27/May/17

x=2nπ+(π/3) .

$${x}=\mathrm{2}{n}\pi+\frac{\pi}{\mathrm{3}}\:. \\ $$

Commented by Tinkutara last updated on 27/May/17

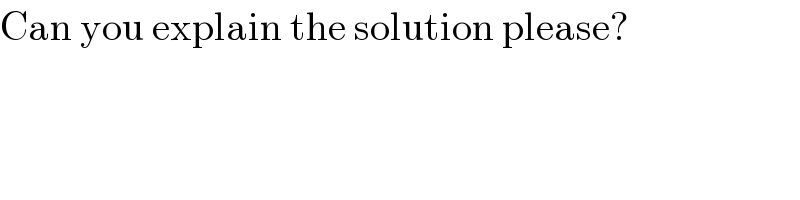
Can you explain the solution please?

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{please}? \\ $$

Answered by ajfour last updated on 27/May/17

above equation implies that cos 3x=−1 and sin (2x−((7π)/6))=−1 ⇒3x=π+2kπ ; k ∈ Z x=(π/3)+k(((2π)/3)) .....(i) also 2x−((7π)/6)=2nπ−(π/2) ⇒ x=(π/3)+nπ .....(ii) for eqns. (i) and (ii) to be simultaneously true: x=2n𝛑+𝛑/3 .

$${above}\:{equation}\:{implies}\:{that} \\ $$$$\mathrm{cos}\:\mathrm{3}{x}=−\mathrm{1}\:\:{and}\:\mathrm{sin}\:\left(\mathrm{2}{x}−\frac{\mathrm{7}\pi}{\mathrm{6}}\right)=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{3}{x}=\pi+\mathrm{2}{k}\pi\:;\:{k}\:\in\:{Z} \\ $$$$\:\:\:\:\:\:\:{x}=\frac{\pi}{\mathrm{3}}+{k}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\:\:\:\:\:\:.....\left({i}\right) \\ $$$${also}\:\:\mathrm{2}{x}−\frac{\mathrm{7}\pi}{\mathrm{6}}=\mathrm{2}{n}\pi−\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=\frac{\pi}{\mathrm{3}}+{n}\pi\:\:\:.....\left({ii}\right) \\ $$$$\:{for}\:{eqns}.\:\left({i}\right)\:{and}\:\left({ii}\right)\:{to}\:{be} \\ $$$${simultaneously}\:{true}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{x}}=\mathrm{2}\boldsymbol{{n}\pi}+\boldsymbol{\pi}/\mathrm{3}\:. \\ $$

Commented by Tinkutara last updated on 27/May/17

But since cos 3x = −1 = cos π, ∴ 3x = 2nπ ± π and similarly sin x = sin y implies x = nπ + (−1)^n y Why you don′t use these conditions?

$$\mathrm{But}\:\mathrm{since}\:\mathrm{cos}\:\mathrm{3}{x}\:=\:−\mathrm{1}\:=\:\mathrm{cos}\:\pi, \\ $$$$\therefore\:\mathrm{3}{x}\:=\:\mathrm{2}{n}\pi\:\pm\:\pi \\ $$$$\mathrm{and}\:\mathrm{similarly}\:\mathrm{sin}\:{x}\:=\:\mathrm{sin}\:{y}\:\mathrm{implies} \\ $$$${x}\:=\:{n}\pi\:+\:\left(−\mathrm{1}\right)^{{n}} \:{y} \\ $$$$\mathrm{Why}\:\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{use}\:\mathrm{these}\:\mathrm{conditions}? \\ $$

Commented by ajfour last updated on 27/May/17

Commented by mrW1 last updated on 27/May/17

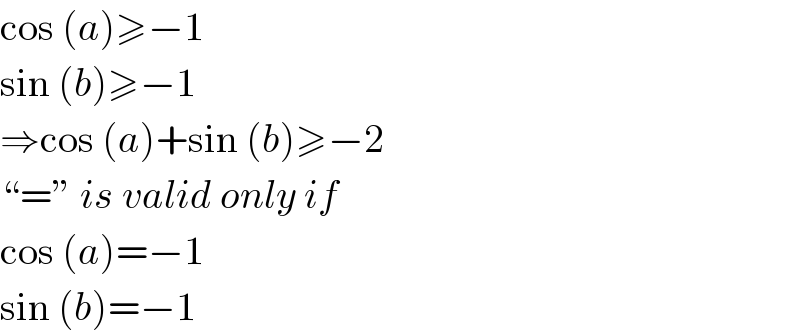
cos (a)≥−1 sin (b)≥−1 ⇒cos (a)+sin (b)≥−2 “=” is valid only if cos (a)=−1 sin (b)=−1

$$\mathrm{cos}\:\left({a}\right)\geqslant−\mathrm{1} \\ $$$$\mathrm{sin}\:\left({b}\right)\geqslant−\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:\left({a}\right)+\mathrm{sin}\:\left({b}\right)\geqslant−\mathrm{2} \\ $$$$``=''\:{is}\:{valid}\:{only}\:{if} \\ $$$$\mathrm{cos}\:\left({a}\right)=−\mathrm{1} \\ $$$$\mathrm{sin}\:\left({b}\right)=−\mathrm{1} \\ $$

Commented by RasheedSindhi last updated on 27/May/17

above equation implies^(?) that cos 3x=−1 and sin (2x−((7π)/6))=−1 −−−−−−−−−−−−− Why the above eq implies? a+b=c[=d+e (say) ] ⇒a=d∧b=e?

$${above}\:{equation}\:\overset{?} {{implies}}\:{that} \\ $$$$\mathrm{cos}\:\mathrm{3}{x}=−\mathrm{1}\:\:{and}\:\mathrm{sin}\:\left(\mathrm{2}{x}−\frac{\mathrm{7}\pi}{\mathrm{6}}\right)=−\mathrm{1} \\ $$$$−−−−−−−−−−−−− \\ $$$$\mathrm{Why}\:\mathrm{the}\:\mathrm{above}\:\mathrm{eq}\:\mathrm{implies}? \\ $$$$\mathrm{a}+\mathrm{b}=\mathrm{c}\left[=\mathrm{d}+\mathrm{e}\:\left(\mathrm{say}\right)\:\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{a}=\mathrm{d}\wedge\mathrm{b}=\mathrm{e}? \\ $$

Answered by mrW1 last updated on 27/May/17

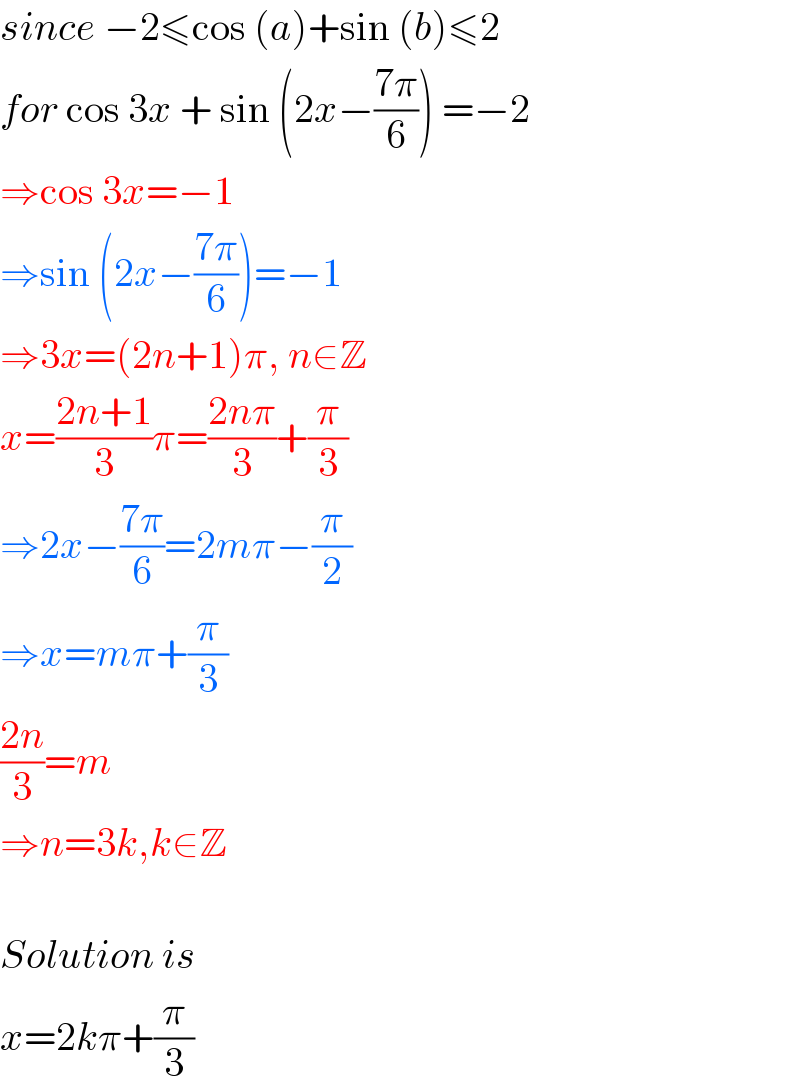
since −2≤cos (a)+sin (b)≤2 for cos 3x + sin (2x−((7π)/6)) =−2 ⇒cos 3x=−1 ⇒sin (2x−((7π)/6))=−1 ⇒3x=(2n+1)π, n∈Z x=((2n+1)/3)π=((2nπ)/3)+(π/3) ⇒2x−((7π)/6)=2mπ−(π/2) ⇒x=mπ+(π/3) ((2n)/3)=m ⇒n=3k,k∈Z Solution is x=2kπ+(π/3)

$${since}\:−\mathrm{2}\leqslant\mathrm{cos}\:\left({a}\right)+\mathrm{sin}\:\left({b}\right)\leqslant\mathrm{2} \\ $$$${for}\:\mathrm{cos}\:\mathrm{3}{x}\:+\:\mathrm{sin}\:\left(\mathrm{2}{x}−\frac{\mathrm{7}\pi}{\mathrm{6}}\right)\:=−\mathrm{2} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{3}{x}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\mathrm{2}{x}−\frac{\mathrm{7}\pi}{\mathrm{6}}\right)=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{3}{x}=\left(\mathrm{2}{n}+\mathrm{1}\right)\pi,\:{n}\in\mathbb{Z} \\ $$$${x}=\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{3}}\pi=\frac{\mathrm{2}{n}\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{2}{x}−\frac{\mathrm{7}\pi}{\mathrm{6}}=\mathrm{2}{m}\pi−\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{x}={m}\pi+\frac{\pi}{\mathrm{3}} \\ $$$$\frac{\mathrm{2}{n}}{\mathrm{3}}={m} \\ $$$$\Rightarrow{n}=\mathrm{3}{k},{k}\in\mathbb{Z} \\ $$$$ \\ $$$${Solution}\:{is} \\ $$$${x}=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{3}} \\ $$

Commented by Tinkutara last updated on 28/May/17

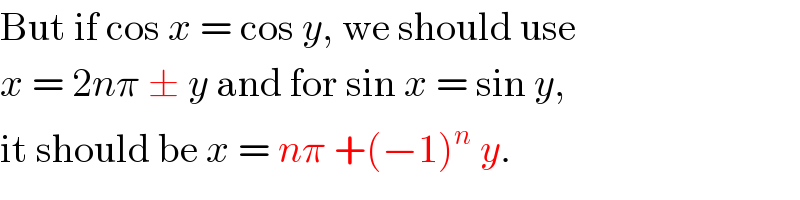
But if cos x = cos y, we should use x = 2nπ ± y and for sin x = sin y, it should be x = nπ +(−1)^n y.

$$\mathrm{But}\:\mathrm{if}\:\mathrm{cos}\:{x}\:=\:\mathrm{cos}\:{y},\:\mathrm{we}\:\mathrm{should}\:\mathrm{use} \\ $$$${x}\:=\:\mathrm{2}{n}\pi\:\pm\:{y}\:\mathrm{and}\:\mathrm{for}\:\mathrm{sin}\:{x}\:=\:\mathrm{sin}\:{y}, \\ $$$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:{x}\:=\:{n}\pi\:+\left(−\mathrm{1}\right)^{{n}} \:{y}. \\ $$

Commented by ajfour last updated on 28/May/17

when we have special values of y such as y=n((π/2)) we should prefer writing in that manner (you are asking justification for). if cos x=−1 x=2kπ+π or x=2nπ±π are equivalent since for n=0, you have x=−π, π both can be obtained with k=−1 and k=0 for n=1, x=π,3π same values obtained with k=0, k=1 what is common to both expressions is that x=(odd integer)×π this only is necessary for cos x=−1. Along similar lines, if sin x=−1 x=2kπ−(π/2) or x=nπ+(−1)^n (−(π/2)) would again be equivalent representations.

$${when}\:{we}\:{have}\:{special}\:{values}\: \\ $$$${of}\:{y}\:{such}\:{as}\:{y}={n}\left(\frac{\pi}{\mathrm{2}}\right)\:{we}\: \\ $$$${should}\:{prefer}\:{writing}\:{in}\:{that} \\ $$$${manner}\:\left({you}\:{are}\:{asking}\right. \\ $$$$\left.{justification}\:{for}\right). \\ $$$$ \\ $$$${if}\:\:\mathrm{cos}\:{x}=−\mathrm{1} \\ $$$${x}=\mathrm{2}{k}\pi+\pi \\ $$$${or}\:\:{x}=\mathrm{2}{n}\pi\pm\pi\:\:\:{are}\:{equivalent} \\ $$$${since}\:{for}\:{n}=\mathrm{0},\:{you}\:{have}\: \\ $$$${x}=−\pi,\:\pi \\ $$$${both}\:{can}\:{be}\:{obtained}\:{with}\:{k}=−\mathrm{1} \\ $$$${and}\:{k}=\mathrm{0} \\ $$$${for}\:{n}=\mathrm{1},\:{x}=\pi,\mathrm{3}\pi \\ $$$${same}\:{values}\:{obtained}\:{with}\:{k}=\mathrm{0}, \\ $$$${k}=\mathrm{1} \\ $$$${what}\:{is}\:{common}\:{to}\:{both}\:{expressions} \\ $$$${is}\:{that}\:{x}=\left({odd}\:{integer}\right)×\pi \\ $$$${this}\:{only}\:{is}\:{necessary}\:{for} \\ $$$$\mathrm{cos}\:{x}=−\mathrm{1}. \\ $$$${Along}\:{similar}\:{lines}, \\ $$$${if}\:\mathrm{sin}\:{x}=−\mathrm{1} \\ $$$${x}=\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{2}} \\ $$$${or}\:{x}={n}\pi+\left(−\mathrm{1}\right)^{{n}} \left(−\frac{\pi}{\mathrm{2}}\right)\:{would}\: \\ $$$${again}\:{be}\:{equivalent}\:{representations}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com