Question Number 141249 by bramlexs22 last updated on 17/May/21
Commented by Rozix last updated on 17/May/21
$${kindly}\:{drop}\:{me}\:{your}\:{whatsapp}\:{numbers}\:{if}\:{interested}\:{in}\:{having}\:{a}\:{maths}\:{group} \\ $$
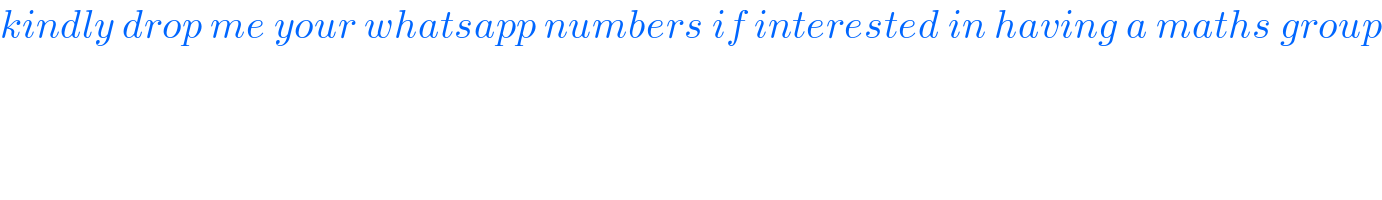
Answered by MJS_new last updated on 17/May/21
![−∫_0 ^(π/2) ((1−cos 2x)/(3+cos 4x))dx= [t=tan x → dx=cos^2 x dt] =−(1/2)∫_0 ^∞ (t^2 /(t^4 +1))dt= =[((√2)/(16))ln ((t^2 +(√2)t+1)/(t^2 −(√2)t+1)) −((√2)/8)(arctan ((√2)t−1) +arctan ((√2)t+1))]_0 ^∞ = =−(((√2)π)/8)](Q141251.png)
$$−\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{3}+\mathrm{cos}\:\mathrm{4}{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\mathrm{cos}^{\mathrm{2}} \:{x}\:{dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} +\mathrm{1}}{dt}= \\ $$$$=\left[\frac{\sqrt{\mathrm{2}}}{\mathrm{16}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\left(\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{t}−\mathrm{1}\right)\:+\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)\right)\right]_{\mathrm{0}} ^{\infty} = \\ $$$$=−\frac{\sqrt{\mathrm{2}}\pi}{\mathrm{8}} \\ $$
Commented by MJS_new last updated on 17/May/21
$$−\frac{\sqrt{\mathrm{2}}\pi}{\mathrm{8}}=−\frac{\sqrt{\mathrm{2}}\pi\sqrt{\mathrm{2}}}{\mathrm{8}\sqrt{\mathrm{2}}}=−\frac{\mathrm{2}\pi}{\mathrm{8}\sqrt{\mathrm{2}}}=−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$
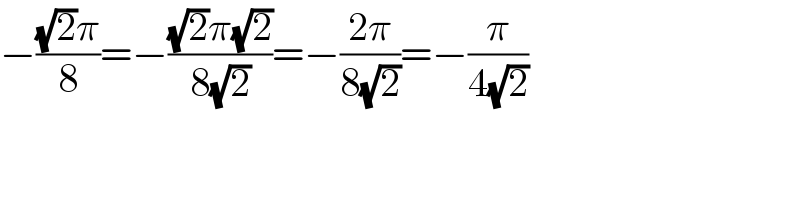
Answered by bemath last updated on 17/May/21
![I=∫_0 ^(π/2) ((cos 2x−1)/(2cos^2 2x+2)) dx 2I=∫_0 ^(π/2) ((cos 2x−1)/(cos^2 2x+1)) let u=(π/2)−x 2I=∫_0 ^(π/2) ((−cos 2x−1)/(cos^2 2x+1)) dx 4I= ∫_0 ^(π/2) ((−2)/(cos^2 2x+1)) dx −2I=∫_0 ^(π/2) ((sec^2 2x)/(sec^2 2x+1)) dx −2I=∫_0 ^(π/2) ((sec^2 2x)/(tan^2 2x +((√2))^2 )) dx −2I=(1/( 2)) ∫_0 ^∞ (dx/(x^2 +((√2))^2 )) −2I=(1/( 2)). (1/( (√2))) [ arctan ((x/( (√2))))]_0 ^∞ I=−(1/(4(√2))).(π/2) = −((π(√2))/8)](Q141268.png)
$${I}=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{cos}\:\mathrm{2}{x}−\mathrm{1}}{\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{2}}\:{dx}\: \\ $$$$\mathrm{2}{I}=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{cos}\:\mathrm{2}{x}−\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{1}} \\ $$$${let}\:{u}=\frac{\pi}{\mathrm{2}}−{x}\: \\ $$$$\mathrm{2}{I}=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{−\mathrm{cos}\:\mathrm{2}{x}−\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{1}}\:{dx} \\ $$$$\mathrm{4}{I}=\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{−\mathrm{2}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{1}}\:{dx} \\ $$$$−\mathrm{2}{I}=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{2}{x}}{\mathrm{sec}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{1}}\:{dx} \\ $$$$−\mathrm{2}{I}=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{2}{x}}{\mathrm{tan}\:^{\mathrm{2}} \mathrm{2}{x}\:+\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\:{dx} \\ $$$$−\mathrm{2}{I}=\frac{\mathrm{1}}{\:\mathrm{2}}\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{{dx}}{{x}^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$−\mathrm{2}{I}=\frac{\mathrm{1}}{\:\mathrm{2}}.\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\left[\:\mathrm{arctan}\:\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{\infty} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}.\frac{\pi}{\mathrm{2}}\:=\:−\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$