
Question Number 141328 by mnjuly1970 last updated on 17/May/21
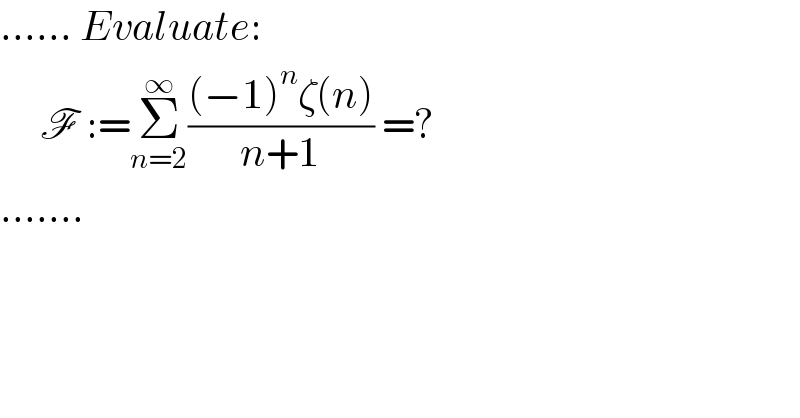
$$......\:{Evaluate}: \\ $$$$\:\:\:\:\:\mathscr{F}\::=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \zeta\left({n}\right)}{{n}+\mathrm{1}}\:=? \\ $$$$....... \\ $$
Answered by Dwaipayan Shikari last updated on 17/May/21
![ψ(z+1)=−γ+Σ_(n=2) ^∞ (−1)^n ζ(n)z^(n−1) ∫_0 ^1 zψ(z+1)=−∫_0 ^1 γzdz+Σ_(n=2) ^∞ (((−1)^n ζ(n))/(n+1)) ⇒[logΓ(z+1)]_0 ^1 −∫_0 ^1 log(Γ(z+1))+(γ/2)=Σ_(n=2) ^∞ (−1)^n ((ζ(n))/(n+1)) ⇒∫_0 ^1 log(Γ(z))+log(z)dz+(γ/2)=Σ_(n=2) ^∞ (((−1)^n )/(n+1))ζ(n) −((log(2π))/2)+1+(γ/2)=Σ_(n=2) ^∞ (((−1)^n )/(n+1))ζ(n)=log((e^(1+(γ/2)) /( (√(2π)))))](Q141332.png)
$$\psi\left({z}+\mathrm{1}\right)=−\gamma+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \zeta\left({n}\right){z}^{{n}−\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {z}\psi\left({z}+\mathrm{1}\right)=−\int_{\mathrm{0}} ^{\mathrm{1}} \gamma{zdz}+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \zeta\left({n}\right)}{{n}+\mathrm{1}} \\ $$$$\Rightarrow\left[{log}\Gamma\left({z}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\Gamma\left({z}+\mathrm{1}\right)\right)+\frac{\gamma}{\mathrm{2}}=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\zeta\left({n}\right)}{{n}+\mathrm{1}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left(\Gamma\left({z}\right)\right)+{log}\left({z}\right){dz}+\frac{\gamma}{\mathrm{2}}=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\zeta\left({n}\right) \\ $$$$−\frac{{log}\left(\mathrm{2}\pi\right)}{\mathrm{2}}+\mathrm{1}+\frac{\gamma}{\mathrm{2}}=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\zeta\left({n}\right)={log}\left(\frac{{e}^{\mathrm{1}+\frac{\gamma}{\mathrm{2}}} }{\:\sqrt{\mathrm{2}\pi}}\right) \\ $$
Commented by mnjuly1970 last updated on 17/May/21

$$\:{grateful}\:{mr}\:{payan}. \\ $$$${very}\:{nice}....{thank}\:{you}\:{for}\:{your} \\ $$$${constan}\:{cooperation}... \\ $$
Commented by Dwaipayan Shikari last updated on 17/May/21

$${Thanks}\:{sir} \\ $$
Answered by mnjuly1970 last updated on 17/May/21
![ln(Γ(x+1))=−γx+Σ_(n=2) ^∞ (((−1)^n x^n ζ(n))/n) diff both sides respect to ”x” ψ(x+1)=−γ+Σ(−1)^n x^(n−1) ζ(n) xψ(x+1)=−γx+Σ_(n=2) ^∞ (−1)^n x^n ζ(n) ∫_0 ^1 x((1/x)+ψ(x))dx=−(γ^2 /2)+Σ(−1)^n ζ(n).(1/(n+1)) 1+[xln(Γ(x))]_0 ^1 −∫_0 ^1 ln(Γ(x))dx=((−γ^2 )/2)+F 1+lim_(x→0^+ ) [(xln(Γ(x)))=^? 0]−(1/2)ln(2π))+(γ^2 /2)=F F:=1+(γ^2 /2)−ln(√(2π)) .......✓✓ ? :: lim_(x→0^+ ) (xln(((Γ(x+1))/x)))= =lim_(x→0^+ ) xln(Γ(x+1))−lim_(x→0^+ ) xln(x) =0](Q141343.png)
$$\:\:{ln}\left(\Gamma\left({x}+\mathrm{1}\right)\right)=−\gamma{x}+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \zeta\left({n}\right)}{{n}} \\ $$$$\:\:\:{diff}\:{both}\:{sides}\:{respect}\:{to}\:''{x}'' \\ $$$$\:\:\:\psi\left({x}+\mathrm{1}\right)=−\gamma+\Sigma\left(−\mathrm{1}\right)^{{n}} {x}^{{n}−\mathrm{1}} \zeta\left({n}\right) \\ $$$${x}\psi\left({x}+\mathrm{1}\right)=−\gamma{x}+\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \zeta\left({n}\right) \\ $$$$\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left(\frac{\mathrm{1}}{{x}}+\psi\left({x}\right)\right){dx}=−\frac{\gamma^{\mathrm{2}} }{\mathrm{2}}+\Sigma\left(−\mathrm{1}\right)^{{n}} \zeta\left({n}\right).\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\:\:\mathrm{1}+\left[{xln}\left(\Gamma\left({x}\right)\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\Gamma\left({x}\right)\right){dx}=\frac{−\gamma^{\mathrm{2}} }{\mathrm{2}}+\mathscr{F} \\ $$$$\left.\mathrm{1}+{lim}_{{x}\rightarrow\mathrm{0}^{+} } \left[\left({xln}\left(\Gamma\left({x}\right)\right)\right)\overset{?} {=}\mathrm{0}\right]−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\pi\right)\right)+\frac{\gamma^{\mathrm{2}} }{\mathrm{2}}=\mathscr{F} \\ $$$$\:\:\mathscr{F}:=\mathrm{1}+\frac{\gamma^{\mathrm{2}} }{\mathrm{2}}−{ln}\sqrt{\mathrm{2}\pi}\:.......\checkmark\checkmark \\ $$$$\:\:\:?\:::\:\:{lim}_{{x}\rightarrow\mathrm{0}^{+} } \left({xln}\left(\frac{\Gamma\left({x}+\mathrm{1}\right)}{{x}}\right)\right)= \\ $$$$\:\:\:\:\:\:\:\:\:={lim}_{{x}\rightarrow\mathrm{0}^{+} } {xln}\left(\Gamma\left({x}+\mathrm{1}\right)\right)−{lim}_{{x}\rightarrow\mathrm{0}^{+} } {xln}\left({x}\right) \\ $$$$\:\:=\mathrm{0} \\ $$$$ \\ $$
