Question and Answers Forum

All Questions      Topic List

Probability and Statistics Questions

Previous in All Question      Next in All Question      

Previous in Probability and Statistics      Next in Probability and Statistics      

Question Number 141409 by Willson last updated on 18/May/21

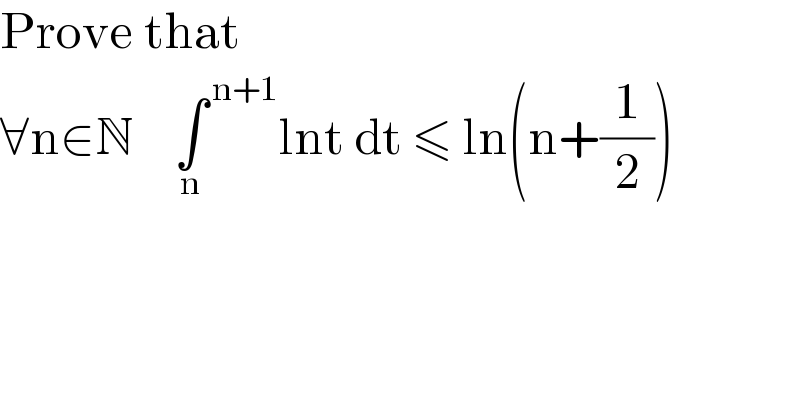
Prove that ∀n∈N ∫^( n+1) _n lnt dt ≤ ln(n+(1/2))

$$\mathrm{Prove}\:\mathrm{that}\: \\ $$$$\forall\mathrm{n}\in\mathbb{N}\:\:\:\:\underset{\mathrm{n}} {\int}^{\:\mathrm{n}+\mathrm{1}} \mathrm{lnt}\:\mathrm{dt}\:\leqslant\:\mathrm{ln}\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$

Answered by TheSupreme last updated on 19/May/21

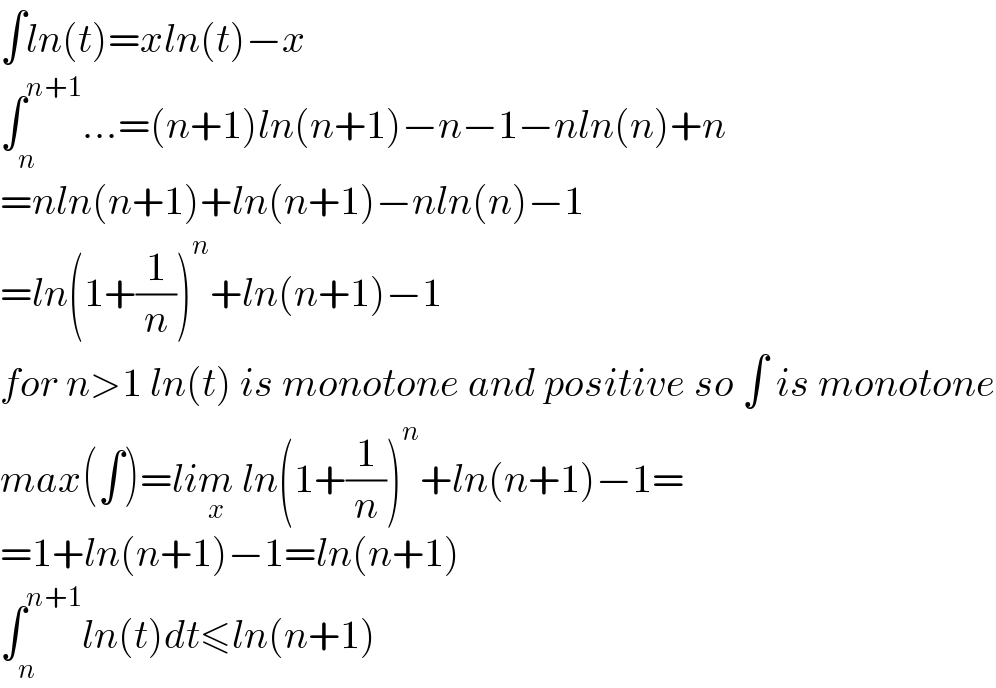
∫ln(t)=xln(t)−x ∫_n ^(n+1) ...=(n+1)ln(n+1)−n−1−nln(n)+n =nln(n+1)+ln(n+1)−nln(n)−1 =ln(1+(1/n))^n +ln(n+1)−1 for n>1 ln(t) is monotone and positive so ∫ is monotone max(∫)=lim_x ln(1+(1/n))^n +ln(n+1)−1= =1+ln(n+1)−1=ln(n+1) ∫_n ^(n+1) ln(t)dt≤ln(n+1)

$$\int{ln}\left({t}\right)={xln}\left({t}\right)−{x} \\ $$$$\int_{{n}} ^{{n}+\mathrm{1}} ...=\left({n}+\mathrm{1}\right){ln}\left({n}+\mathrm{1}\right)−{n}−\mathrm{1}−{nln}\left({n}\right)+{n} \\ $$$$={nln}\left({n}+\mathrm{1}\right)+{ln}\left({n}+\mathrm{1}\right)−{nln}\left({n}\right)−\mathrm{1} \\ $$$$={ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} +{ln}\left({n}+\mathrm{1}\right)−\mathrm{1} \\ $$$${for}\:{n}>\mathrm{1}\:{ln}\left({t}\right)\:{is}\:{monotone}\:{and}\:{positive}\:{so}\:\int\:{is}\:{monotone} \\ $$$${max}\left(\int\right)={li}\underset{{x}} {{m}}\:{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} +{ln}\left({n}+\mathrm{1}\right)−\mathrm{1}= \\ $$$$=\mathrm{1}+{ln}\left({n}+\mathrm{1}\right)−\mathrm{1}={ln}\left({n}+\mathrm{1}\right) \\ $$$$\int_{{n}} ^{{n}+\mathrm{1}} {ln}\left({t}\right){dt}\leqslant{ln}\left({n}+\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com