
Question and Answers Forum
Question Number 141417 by mnjuly1970 last updated on 18/May/21
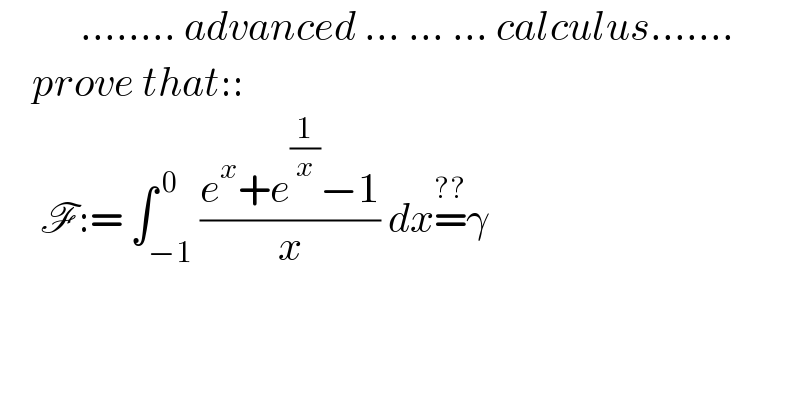
Answered by mnjuly1970 last updated on 27/May/21
![:=∫_(−1 ) ^( 0) (e^(1/x) /x)dx=^((1/x)=−y) ∫_1 ^( ∞) −ye^(−y) (dy/y^2 ) := −∫_1 ^( ∞) (e^(−y) /y)dy=−∫_1 ^( ∞) e^(−y) ln(y)−[ln(y)e^(−y) ]_1 ^∞ :=−∫_1 ^( ∞) e^(−y) ln(y)dy⇒−∫_0 ^( ∞) e^(−y) ln(y)dy+∫_0 ^( 1) e^(−y) ln(y)dy ∫_(−1) ^( 0) (e^(1/x) /x)dx:= γ+∫_0 ^( 1) e^(−x) ln(x)dx (★) := γ +∫_0 ^( 1) ln(x)d(1−e^(−x) ) := γ+[ln(x)(1−e^(−x) )]_0 ^( 1) −∫_0 ^( 1) (((1−e^(−x) )/x))dx := γ −∫_0 ^( 1) ((1−e^(−x) )/x)dx=γ+∫_0 ^( −1) ((1−e^x )/(−x))dx :=γ +∫_(−1) ^( 0) ((1−e^x )/x) dx (★) :: ∫_(−1) ^( 0) ((e^(1/x) +e^x −1)/x) =γ .....✓ ........ F := ∫_(−1) ^( 0) ((e^x +e^(1/x) −1)/x) dx = γ ......](Q142213.png)
Answered by mindispower last updated on 19/May/21
![x=(1/t)⇒F=∫_(−1) ^0 ((e^x −1)/x)dx+∫_(−1) ^0 (e^(1/x) /x)dx=A+B A=[e^x −1]ln(−x)]_(−1) ^0 −∫_(−1) ^0 e^x ln(−x) =−∫_(−1) ^0 e^x ln(−x)dx=∫_1 ^0 e^(−t) ln(t)dt B=[ln(−x)e^(1/x) ]_(−1) ^0 −∫_(−1) ^0 (e^(1/x) /x^2 )ln(−x)dx =∫_(−1) ^0 −(e^(1/x) /x^2 )ln(−x),t=−(1/x)⇒ B=−∫_1 ^∞ e^(−t) ln(t) F=A+B=−∫_0 ^∞ ln(t)e^(−t) dt=∂_x (−∫_0 ^∞ e^(−t) t^(x−1) dt)∣_(x=1) =∂_x .−Γ(x+1)∣_(x=0) =−Γ′(1)=−Γ(1)Ψ(1)=−1.−γ=γ ⇒∫_(−1) ^0 ((e^x +e^(1/x) −1)/x)dx=γ](Q141514.png)
| ||
Question and Answers Forum | ||
Question Number 141417 by mnjuly1970 last updated on 18/May/21 | ||
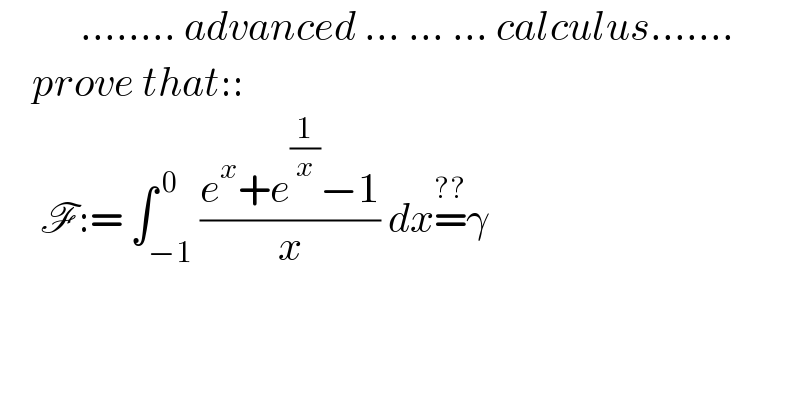 | ||
Answered by mnjuly1970 last updated on 27/May/21 | ||
![:=∫_(−1 ) ^( 0) (e^(1/x) /x)dx=^((1/x)=−y) ∫_1 ^( ∞) −ye^(−y) (dy/y^2 ) := −∫_1 ^( ∞) (e^(−y) /y)dy=−∫_1 ^( ∞) e^(−y) ln(y)−[ln(y)e^(−y) ]_1 ^∞ :=−∫_1 ^( ∞) e^(−y) ln(y)dy⇒−∫_0 ^( ∞) e^(−y) ln(y)dy+∫_0 ^( 1) e^(−y) ln(y)dy ∫_(−1) ^( 0) (e^(1/x) /x)dx:= γ+∫_0 ^( 1) e^(−x) ln(x)dx (★) := γ +∫_0 ^( 1) ln(x)d(1−e^(−x) ) := γ+[ln(x)(1−e^(−x) )]_0 ^( 1) −∫_0 ^( 1) (((1−e^(−x) )/x))dx := γ −∫_0 ^( 1) ((1−e^(−x) )/x)dx=γ+∫_0 ^( −1) ((1−e^x )/(−x))dx :=γ +∫_(−1) ^( 0) ((1−e^x )/x) dx (★) :: ∫_(−1) ^( 0) ((e^(1/x) +e^x −1)/x) =γ .....✓ ........ F := ∫_(−1) ^( 0) ((e^x +e^(1/x) −1)/x) dx = γ ......](Q142213.png) | ||
| ||
Answered by mindispower last updated on 19/May/21 | ||
![x=(1/t)⇒F=∫_(−1) ^0 ((e^x −1)/x)dx+∫_(−1) ^0 (e^(1/x) /x)dx=A+B A=[e^x −1]ln(−x)]_(−1) ^0 −∫_(−1) ^0 e^x ln(−x) =−∫_(−1) ^0 e^x ln(−x)dx=∫_1 ^0 e^(−t) ln(t)dt B=[ln(−x)e^(1/x) ]_(−1) ^0 −∫_(−1) ^0 (e^(1/x) /x^2 )ln(−x)dx =∫_(−1) ^0 −(e^(1/x) /x^2 )ln(−x),t=−(1/x)⇒ B=−∫_1 ^∞ e^(−t) ln(t) F=A+B=−∫_0 ^∞ ln(t)e^(−t) dt=∂_x (−∫_0 ^∞ e^(−t) t^(x−1) dt)∣_(x=1) =∂_x .−Γ(x+1)∣_(x=0) =−Γ′(1)=−Γ(1)Ψ(1)=−1.−γ=γ ⇒∫_(−1) ^0 ((e^x +e^(1/x) −1)/x)dx=γ](Q141514.png) | ||
| ||