
Question and Answers Forum
Question Number 141496 by cesarL last updated on 19/May/21

Answered by qaz last updated on 19/May/21
Answered by MJS_new last updated on 19/May/21
![∫((√(a^2 x^2 +b^2 ))/x)dx= [x=((b(t^2 −1))/(2at)) ⇔ t=((ax+(√(a^2 x^2 +b^2 )))/b) → dx=((b(√(a^2 x^2 +b^2 )))/(a(ax+(√(a^2 x^2 +b^2 )))))dt] =(b/2)∫(((t^2 +1)^2 )/(t^2 (t^2 −1)))dt= =(b/2)∫((t^2 −1)/t^2 )dt+b∫(dt/(t−1))−b∫(dt/(t+1))= =((b(t^2 +1))/(2t))+bln ((t−1)/(t+1))= =(√(a^2 x^2 +b^2 ))+bln ∣((b−(√(a^2 x^2 +b^2 )))/x)∣ +C](Q141506.png)
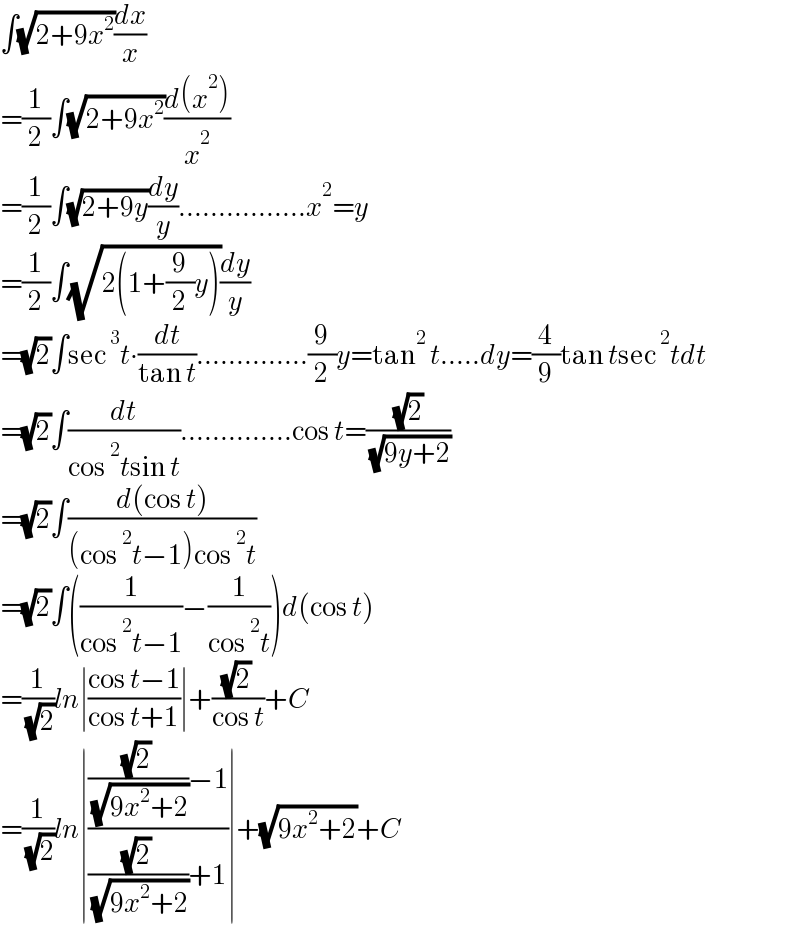
Answered by mathmax by abdo last updated on 20/May/21

| ||
Question and Answers Forum | ||
Question Number 141496 by cesarL last updated on 19/May/21 | ||
 | ||
Answered by qaz last updated on 19/May/21 | ||
 | ||
| ||
Answered by MJS_new last updated on 19/May/21 | ||
![∫((√(a^2 x^2 +b^2 ))/x)dx= [x=((b(t^2 −1))/(2at)) ⇔ t=((ax+(√(a^2 x^2 +b^2 )))/b) → dx=((b(√(a^2 x^2 +b^2 )))/(a(ax+(√(a^2 x^2 +b^2 )))))dt] =(b/2)∫(((t^2 +1)^2 )/(t^2 (t^2 −1)))dt= =(b/2)∫((t^2 −1)/t^2 )dt+b∫(dt/(t−1))−b∫(dt/(t+1))= =((b(t^2 +1))/(2t))+bln ((t−1)/(t+1))= =(√(a^2 x^2 +b^2 ))+bln ∣((b−(√(a^2 x^2 +b^2 )))/x)∣ +C](Q141506.png) | ||
| ||
Answered by mathmax by abdo last updated on 20/May/21 | ||
 | ||
| ||