
Question and Answers Forum
Question Number 141525 by hgrocks last updated on 20/May/21
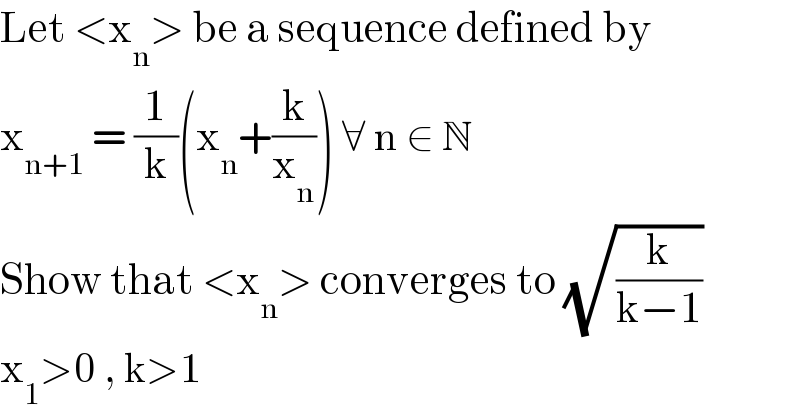
Answered by mathmax by abdo last updated on 21/May/21
![x_(n+1) =f(x_n ) with f(x)=(1/k)(x+(k/x)) f is continue on R^★ f^′ (x)=(1/k)(1−(k/x^2 )) =(1/k)×((x^2 −k)/x^2 ) =(1/(kx^2 ))(x−(√k))(x+(√k)) we can limit the variation on ]0,+∞[ due to u_n >0 for all n x 0 (√k) +∞ f^′ ∣ ∣ − 0 + f ∣ ∣ dec f((√k)) incr +∞ due to continuity of f the limit of u_(n ) is the fix point of f f(x)=x ⇒(1/k)(x+(k/x))=x ⇒x^2 +k=kx^2 ⇒(k−1)x^2 =k ⇒ but x>0 ⇒x=(√(k/(k−1)))( k>1)](Q141625.png)
Commented byhgrocks last updated on 21/May/21

| ||
Question and Answers Forum | ||
Question Number 141525 by hgrocks last updated on 20/May/21 | ||
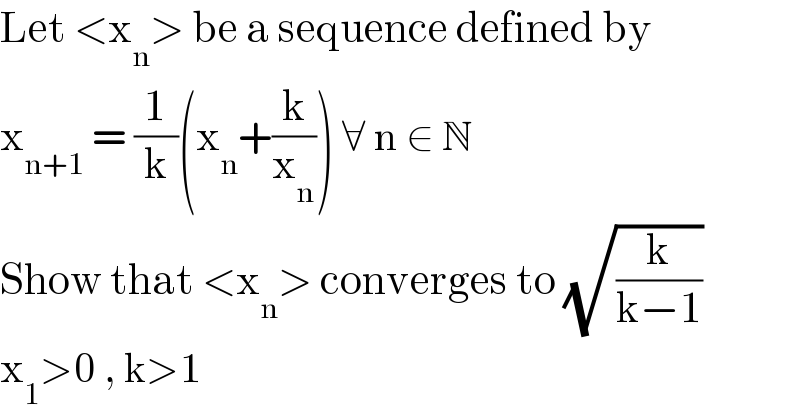 | ||
Answered by mathmax by abdo last updated on 21/May/21 | ||
![x_(n+1) =f(x_n ) with f(x)=(1/k)(x+(k/x)) f is continue on R^★ f^′ (x)=(1/k)(1−(k/x^2 )) =(1/k)×((x^2 −k)/x^2 ) =(1/(kx^2 ))(x−(√k))(x+(√k)) we can limit the variation on ]0,+∞[ due to u_n >0 for all n x 0 (√k) +∞ f^′ ∣ ∣ − 0 + f ∣ ∣ dec f((√k)) incr +∞ due to continuity of f the limit of u_(n ) is the fix point of f f(x)=x ⇒(1/k)(x+(k/x))=x ⇒x^2 +k=kx^2 ⇒(k−1)x^2 =k ⇒ but x>0 ⇒x=(√(k/(k−1)))( k>1)](Q141625.png) | ||
| ||
Commented byhgrocks last updated on 21/May/21 | ||
 | ||