Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 141585 by ZiYangLee last updated on 20/May/21

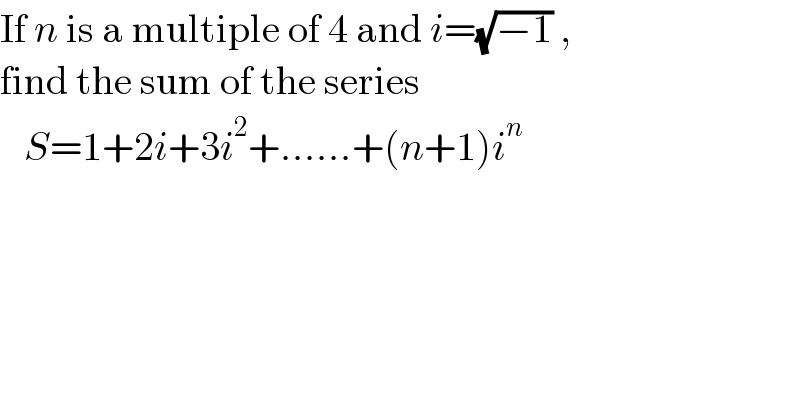
If n is a multiple of 4 and i=(√(−1)) , find the sum of the series S=1+2i+3i^2 +......+(n+1)i^n

$$\mathrm{If}\:{n}\:\mathrm{is}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{4}\:\mathrm{and}\:{i}=\sqrt{−\mathrm{1}}\:,\: \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{series} \\ $$$$\:\:\:{S}=\mathrm{1}+\mathrm{2}{i}+\mathrm{3}{i}^{\mathrm{2}} +......+\left({n}+\mathrm{1}\right){i}^{{n}} \: \\ $$

Answered by mathmax by abdo last updated on 21/May/21

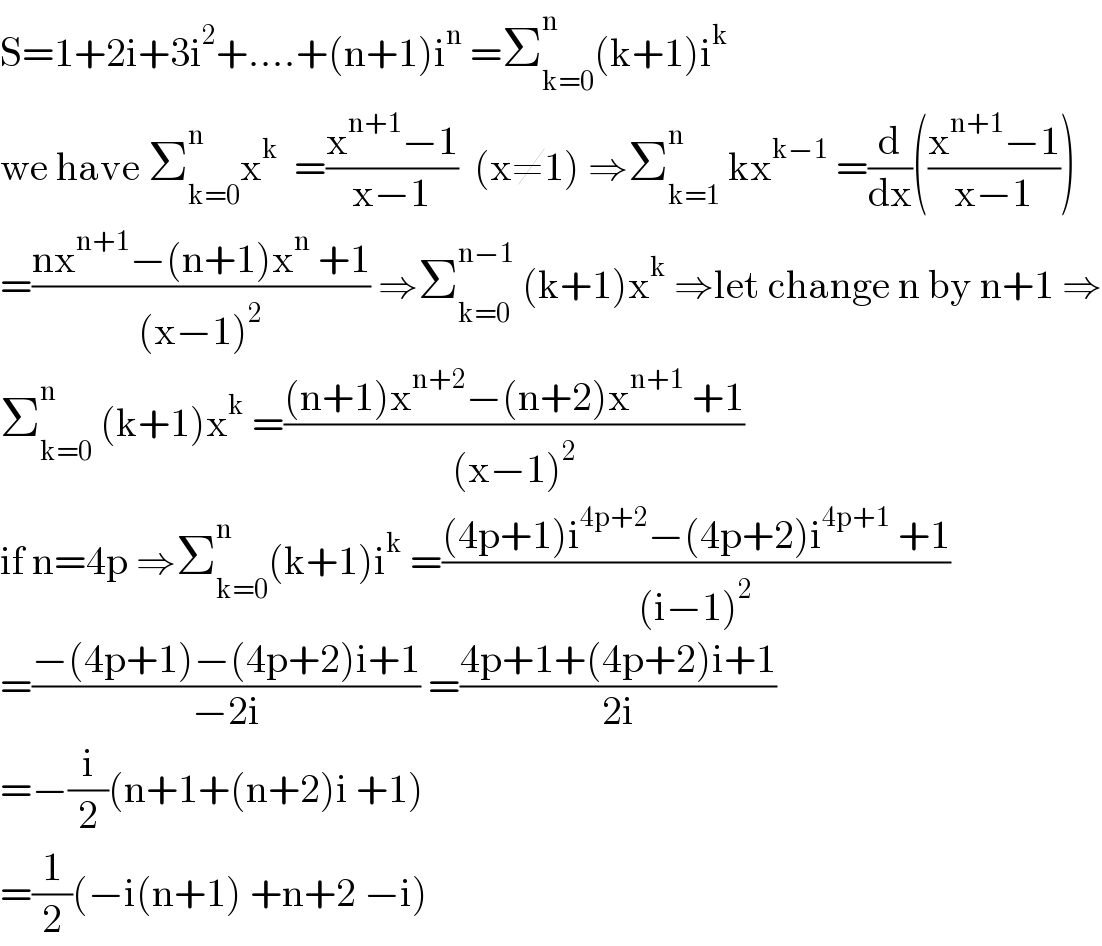
S=1+2i+3i^2 +....+(n+1)i^n =Σ_(k=0) ^n (k+1)i^k we have Σ_(k=0) ^n x^k =((x^(n+1) −1)/(x−1)) (x≠1) ⇒Σ_(k=1) ^n kx^(k−1) =(d/dx)(((x^(n+1) −1)/(x−1))) =((nx^(n+1) −(n+1)x^n +1)/((x−1)^2 )) ⇒Σ_(k=0) ^(n−1) (k+1)x^k ⇒let change n by n+1 ⇒ Σ_(k=0) ^n (k+1)x^k =(((n+1)x^(n+2) −(n+2)x^(n+1) +1)/((x−1)^2 )) if n=4p ⇒Σ_(k=0) ^n (k+1)i^k =(((4p+1)i^(4p+2) −(4p+2)i^(4p+1) +1)/((i−1)^2 )) =((−(4p+1)−(4p+2)i+1)/(−2i)) =((4p+1+(4p+2)i+1)/(2i)) =−(i/2)(n+1+(n+2)i +1) =(1/2)(−i(n+1) +n+2 −i)

$$\mathrm{S}=\mathrm{1}+\mathrm{2i}+\mathrm{3i}^{\mathrm{2}} +....+\left(\mathrm{n}+\mathrm{1}\right)\mathrm{i}^{\mathrm{n}} \:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \left(\mathrm{k}+\mathrm{1}\right)\mathrm{i}^{\mathrm{k}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \mathrm{x}^{\mathrm{k}} \:\:=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{x}−\mathrm{1}}\:\:\left(\mathrm{x}\neq\mathrm{1}\right)\:\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{kx}^{\mathrm{k}−\mathrm{1}} \:=\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{x}−\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{nx}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} \:+\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\left(\mathrm{k}+\mathrm{1}\right)\mathrm{x}^{\mathrm{k}} \:\Rightarrow\mathrm{let}\:\mathrm{change}\:\mathrm{n}\:\mathrm{by}\:\mathrm{n}+\mathrm{1}\:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\left(\mathrm{k}+\mathrm{1}\right)\mathrm{x}^{\mathrm{k}} \:=\frac{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}+\mathrm{2}} −\left(\mathrm{n}+\mathrm{2}\right)\mathrm{x}^{\mathrm{n}+\mathrm{1}} \:+\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{if}\:\mathrm{n}=\mathrm{4p}\:\Rightarrow\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \left(\mathrm{k}+\mathrm{1}\right)\mathrm{i}^{\mathrm{k}} \:=\frac{\left(\mathrm{4p}+\mathrm{1}\right)\mathrm{i}^{\mathrm{4p}+\mathrm{2}} −\left(\mathrm{4p}+\mathrm{2}\right)\mathrm{i}^{\mathrm{4p}+\mathrm{1}} \:+\mathrm{1}}{\left(\mathrm{i}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{−\left(\mathrm{4p}+\mathrm{1}\right)−\left(\mathrm{4p}+\mathrm{2}\right)\mathrm{i}+\mathrm{1}}{−\mathrm{2i}}\:=\frac{\mathrm{4p}+\mathrm{1}+\left(\mathrm{4p}+\mathrm{2}\right)\mathrm{i}+\mathrm{1}}{\mathrm{2i}} \\ $$$$=−\frac{\mathrm{i}}{\mathrm{2}}\left(\mathrm{n}+\mathrm{1}+\left(\mathrm{n}+\mathrm{2}\right)\mathrm{i}\:+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{i}\left(\mathrm{n}+\mathrm{1}\right)\:+\mathrm{n}+\mathrm{2}\:−\mathrm{i}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com