
Question and Answers Forum
Question Number 141716 by qaz last updated on 22/May/21
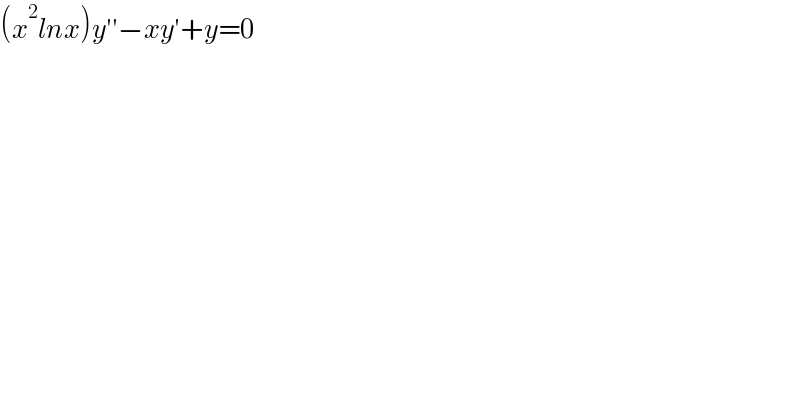
Answered by mnjuly1970 last updated on 23/May/21
![y_p_1 =ln(x)+1 or y_p_1 =x consider : y_p_1 =1+ln(x) because :: (x^2 ln(x))[((−1)/x^2 )]−x((1/x))+ln(x)+1=0 y_p_2 =v(x).y_p_1 where : v(x)=∫(1/((1+ln(x))^2 ))e^(∫(1/(xln(x)))dx) dx =∫(1/((1+ln(x))^2 ))e^(∫((1/x)/(ln(x)))dx) =∫ (e^(ln(ln(x)) /((1+ln(x))^2 ))dx =∫((ln(x))/((1+ln(x))^2 ))dx=^(ln(x)=t) ∫((te^t )/((1+t)^2 ))dt =∫[((1+t−1)/((1+t)^2 )).e^t ]dt=∫[(1/(1+t))−(1/((1+t)^2 ))]e^t dt =(e^t /(1+t))⇒ v(x)=(x/(1+ln(x))) y_p_2 =v(x).y_p_1 =(x/((1+ln(x))))(1+ln(x))=x .... y_c =c_1 (1+ln(x))+c_2 x..... general solution ....⇑⇑⇑](Q141751.png)
| ||
Question and Answers Forum | ||
Question Number 141716 by qaz last updated on 22/May/21 | ||
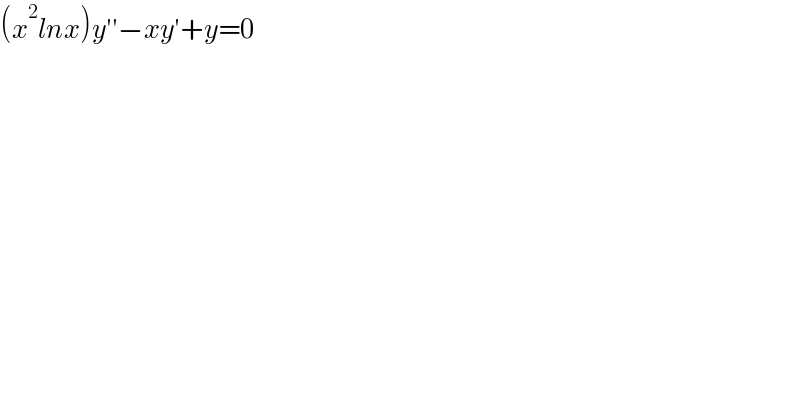 | ||
Answered by mnjuly1970 last updated on 23/May/21 | ||
![y_p_1 =ln(x)+1 or y_p_1 =x consider : y_p_1 =1+ln(x) because :: (x^2 ln(x))[((−1)/x^2 )]−x((1/x))+ln(x)+1=0 y_p_2 =v(x).y_p_1 where : v(x)=∫(1/((1+ln(x))^2 ))e^(∫(1/(xln(x)))dx) dx =∫(1/((1+ln(x))^2 ))e^(∫((1/x)/(ln(x)))dx) =∫ (e^(ln(ln(x)) /((1+ln(x))^2 ))dx =∫((ln(x))/((1+ln(x))^2 ))dx=^(ln(x)=t) ∫((te^t )/((1+t)^2 ))dt =∫[((1+t−1)/((1+t)^2 )).e^t ]dt=∫[(1/(1+t))−(1/((1+t)^2 ))]e^t dt =(e^t /(1+t))⇒ v(x)=(x/(1+ln(x))) y_p_2 =v(x).y_p_1 =(x/((1+ln(x))))(1+ln(x))=x .... y_c =c_1 (1+ln(x))+c_2 x..... general solution ....⇑⇑⇑](Q141751.png) | ||
| ||