Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 141794 by mathdanisur last updated on 23/May/21

Commented by JDamian last updated on 23/May/21

$r e p e a t e d q u e s t i o n 141730$
Commented by mathdanisur last updated on 23/May/21

$s o l u t i o n, n o a n s w e r$
	Answered by MJS_new last updated on 23/May/21

	$my path :$ $let y = p x \land z = q x$ $(1) (p^{2} + p + 1) x^{2} = 9$ $(2) (p^{2} + p q + q^{2}) x^{2} = 16$ $(3) (q^{2} + q + 1) x^{2} = 25$ $\Rightarrow$ $\frac{p^{2} + p + 1}{9} = \frac{p^{2} + p q + q^{2}}{16} = \frac{q^{2} + q + 1}{25}$ $(a) = (b) = (c)$ $from solving (a) = (b) \land (b) = (c) we get$ $q = \frac{- p (2 p + 1)}{p - 1}$ $this leads to (a) = (c)$ $(p^{2} + p + 1) (p^{2} + \frac{32}{11} p - \frac{16}{11}) = 0$ $\Rightarrow p = - \frac{16 + 12 \sqrt{3}}{11} \lor p = \frac{- 16 + 12 \sqrt{3}}{11}$ $now insert backwards$
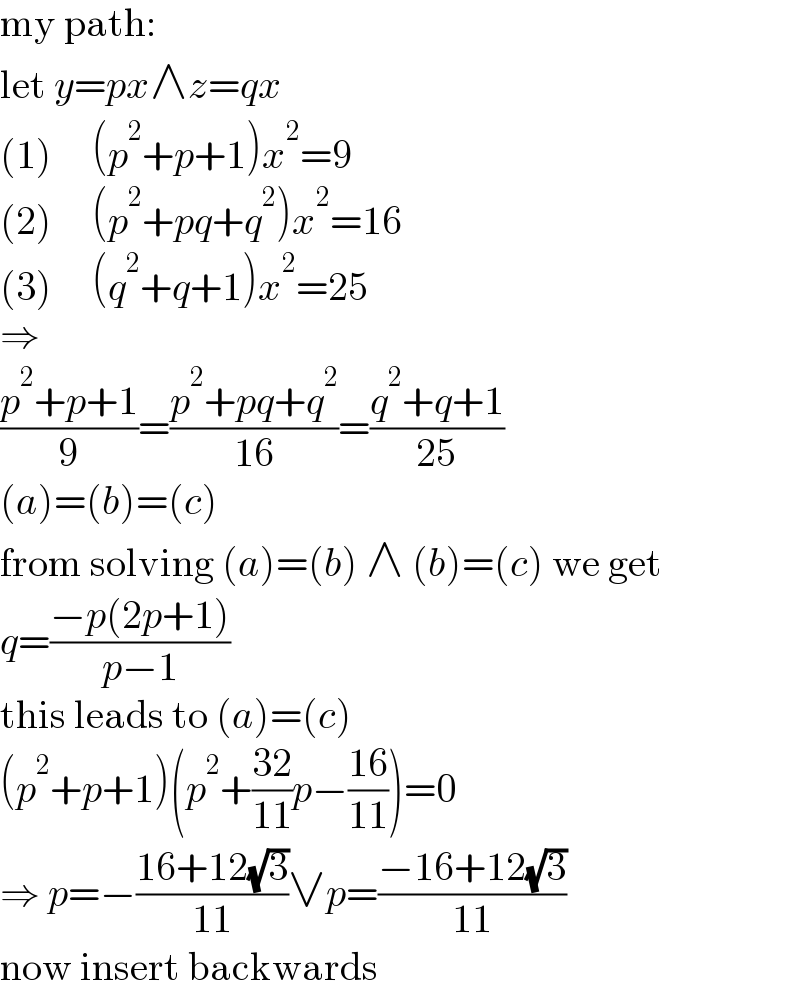
	Answered by mr W last updated on 23/May/21

	$x^{2} + y^{2} + x y = 9 . . . (i)$ $y^{2} + z^{2} + y z = 16 . . . (i i)$ $z^{2} + x^{2} + z x = 25 . . . (i i i)$ $(i i) - (i) :$ $z^{2} - x^{2} + y (z - x) = 7$ $(z - x) (x + y + z) = 7$ $l e t s = x + y + z$ $\Rightarrow z = \frac{7}{s} + x$ $(i i i) - (i i) :$ $(x - y) (x + y + z) = 9$ $\Rightarrow y = - \frac{9}{s} + x$ $x + y + z = x - \frac{9}{s} + x + \frac{7}{s} + x = 3 x - \frac{2}{s} = s$ $\Rightarrow x = \frac{s}{3} + \frac{2}{3 s}$ $\Rightarrow y = - \frac{9}{s} + \frac{s}{3} + \frac{2}{3 s} = \frac{s}{3} - \frac{25}{3 s}$ $i n s e r t i n t o (i) :$ ${(\frac{s}{3} + \frac{2}{3 s})}^{2} + {(\frac{s}{3} - \frac{25}{3 s})}^{2} + (\frac{s}{3} + \frac{2}{3 s}) (\frac{s}{3} - \frac{25}{3 s}) = 9$ $s^{2} - 50 + \frac{193}{s^{2}} = 0$ $s^{4} - 50 s^{2} + 193 = 0$ $\Rightarrow s^{2} = 25 \pm 12 \sqrt{3}$ $(i) + (i i) + (i i i) :$ $2 (x^{2} + y^{2} + z^{2}) + (z y + y z + z x) = 50$ $s^{2} = {(x + y + z)}^{2} = x^{2} + y^{2} + z^{2} + 2 (x y + y z + z x)$ $2 s^{2} = 2 (x^{2} + y^{2} + z^{2}) + x y + y z + z x + 3 (x y + y z + z x)$ $2 (25 \pm 12 \sqrt{3}) = 50 + 3 (x y + y z + z x)$ $\Rightarrow x y + y z + z x = \pm 8 \sqrt{3}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum