Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 1418 by Rasheed Ahmad last updated on 04/Aug/15

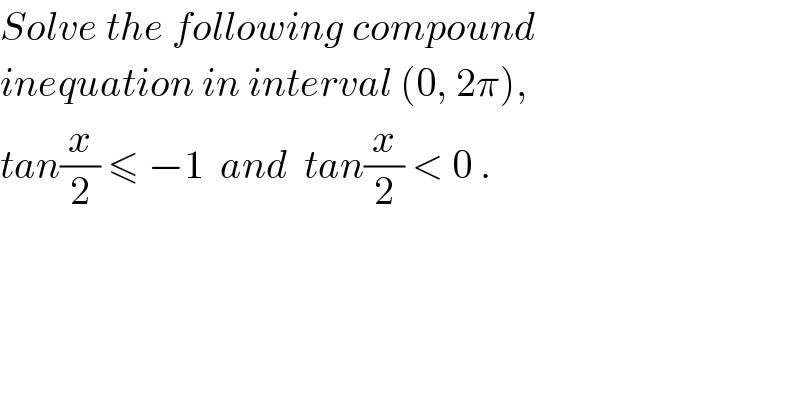
Solve the following compound inequation in interval (0, 2π), tan(x/2) ≤ −1 and tan(x/2) < 0 .

$${Solve}\:{the}\:{following}\:{compound} \\ $$ $${inequation}\:{in}\:{interval}\:\left(\mathrm{0},\:\mathrm{2}\pi\right), \\ $$ $${tan}\frac{{x}}{\mathrm{2}}\:\leqslant\:−\mathrm{1}\:\:{and}\:\:{tan}\frac{{x}}{\mathrm{2}}\:<\:\mathrm{0}\:. \\ $$

Commented by123456 last updated on 31/Jul/15

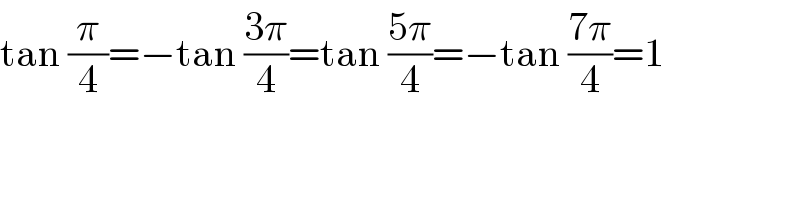
tan (π/4)=−tan ((3π)/4)=tan ((5π)/4)=−tan ((7π)/4)=1

$$\mathrm{tan}\:\frac{\pi}{\mathrm{4}}=−\mathrm{tan}\:\frac{\mathrm{3}\pi}{\mathrm{4}}=\mathrm{tan}\:\frac{\mathrm{5}\pi}{\mathrm{4}}=−\mathrm{tan}\:\frac{\mathrm{7}\pi}{\mathrm{4}}=\mathrm{1} \\ $$

Answered by 123456 last updated on 31/Jul/15

tan (x/2)<0 (x/2)∈((π/2)+2πk,π+2πk)∪(((3π)/2)+2πk,2π+2πk),k∈Z x∈(π+4πk,2π+4πk)∪(3π+4πk,4π+4πk) tan (x/2)≤−1 (x/2)∈((π/2)+2πk,((3π)/4)+2πk]∪(((3π)/2)+2πk,((7π)/4)+2πk] x∈(π+4πk,((3π)/2)+4πk]∪(3π+4πk,((7π)/2)+4πk]

$$\mathrm{tan}\:\frac{{x}}{\mathrm{2}}<\mathrm{0} \\ $$ $$\frac{{x}}{\mathrm{2}}\in\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}\pi{k},\pi+\mathrm{2}\pi{k}\right)\cup\left(\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{2}\pi{k},\mathrm{2}\pi+\mathrm{2}\pi{k}\right),{k}\in\mathbb{Z} \\ $$ $${x}\in\left(\pi+\mathrm{4}\pi{k},\mathrm{2}\pi+\mathrm{4}\pi{k}\right)\cup\left(\mathrm{3}\pi+\mathrm{4}\pi{k},\mathrm{4}\pi+\mathrm{4}\pi{k}\right) \\ $$ $$\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\leqslant−\mathrm{1} \\ $$ $$\frac{{x}}{\mathrm{2}}\in\left(\frac{\pi}{\mathrm{2}}+\mathrm{2}\pi{k},\frac{\mathrm{3}\pi}{\mathrm{4}}+\mathrm{2}\pi{k}\right]\cup\left(\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{2}\pi{k},\frac{\mathrm{7}\pi}{\mathrm{4}}+\mathrm{2}\pi{k}\right] \\ $$ $${x}\in\left(\pi+\mathrm{4}\pi{k},\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{4}\pi{k}\right]\cup\left(\mathrm{3}\pi+\mathrm{4}\pi{k},\frac{\mathrm{7}\pi}{\mathrm{2}}+\mathrm{4}\pi{k}\right] \\ $$

Commented byRasheed Ahmad last updated on 03/Aug/15

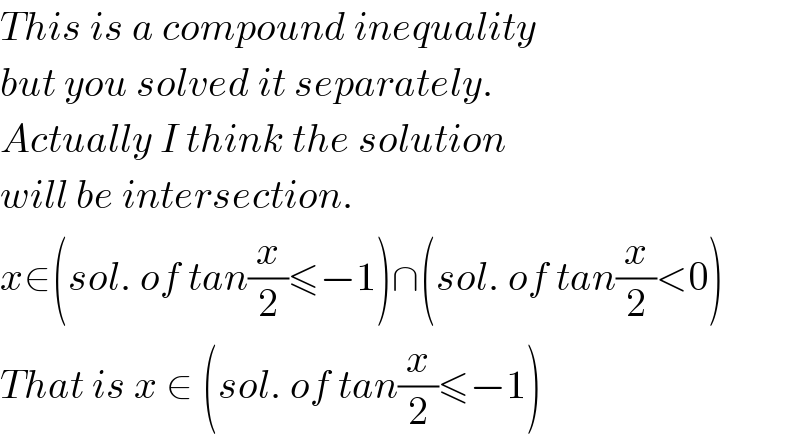
This is a compound inequality but you solved it separately. Actually I think the solution will be intersection. x∈(sol. of tan(x/2)≤−1)∩(sol. of tan(x/2)<0) That is x ∈ (sol. of tan(x/2)≤−1)

$${This}\:{is}\:{a}\:{compound}\:{inequality}\: \\ $$ $${but}\:{you}\:{solved}\:{it}\:{separately}. \\ $$ $${Actually}\:{I}\:{think}\:{the}\:{solution} \\ $$ $${will}\:{be}\:{intersection}. \\ $$ $${x}\in\left({sol}.\:{of}\:{tan}\frac{{x}}{\mathrm{2}}\leqslant−\mathrm{1}\right)\cap\left({sol}.\:{of}\:{tan}\frac{{x}}{\mathrm{2}}<\mathrm{0}\right) \\ $$ $${That}\:{is}\:{x}\:\in\:\left({sol}.\:{of}\:{tan}\frac{{x}}{\mathrm{2}}\leqslant−\mathrm{1}\right) \\ $$

Commented by123456 last updated on 03/Aug/15

yes, i didn′t see it, the solution then is the intersection of these two solution x∈(π+4πk,((3π)/2)+4πk]∪(3π+4πk,((7π)/2)+4πk] for x∈[0,2π) we have x∈(π,((3π)/2)]

$$\mathrm{yes},\:\mathrm{i}\:\mathrm{didn}'\mathrm{t}\:\mathrm{see}\:\mathrm{it},\:\mathrm{the}\:\mathrm{solution}\:\mathrm{then} \\ $$ $$\mathrm{is}\:\mathrm{the}\:\mathrm{intersection}\:\mathrm{of}\:\mathrm{these}\:\mathrm{two}\:\mathrm{solution} \\ $$ $${x}\in\left(\pi+\mathrm{4}\pi{k},\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{4}\pi{k}\right]\cup\left(\mathrm{3}\pi+\mathrm{4}\pi{k},\frac{\mathrm{7}\pi}{\mathrm{2}}+\mathrm{4}\pi{k}\right] \\ $$ $$\mathrm{for}\:{x}\in\left[\mathrm{0},\mathrm{2}\pi\right)\:\mathrm{we}\:\mathrm{have} \\ $$ $${x}\in\left(\pi,\frac{\mathrm{3}\pi}{\mathrm{2}}\right] \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com