
Question and Answers Forum
Question Number 141805 by mohammad17 last updated on 23/May/21

Answered by MJS_new last updated on 23/May/21
![∫(dx/(1−tan x))= [t=tan x → dx=(dt/(t^2 +1))] =∫(dt/((1−t)(t^2 +1)))= =(1/4)∫((2t)/(t^2 +1))dt+(1/2)∫(dt/(t^2 +1))−(1/2)∫(dt/(t−1))= =(1/4)ln (t^2 +1) +(1/2)arctan t −(1/2)ln (t−1) = =(1/4)ln ((t^2 +1)/((t−1)^2 )) +(1/2)arctan t = =(x/2)−(1/4)ln (1−sin 2x) +C](Q141809.png)
Answered by mathmax by abdo last updated on 24/May/21
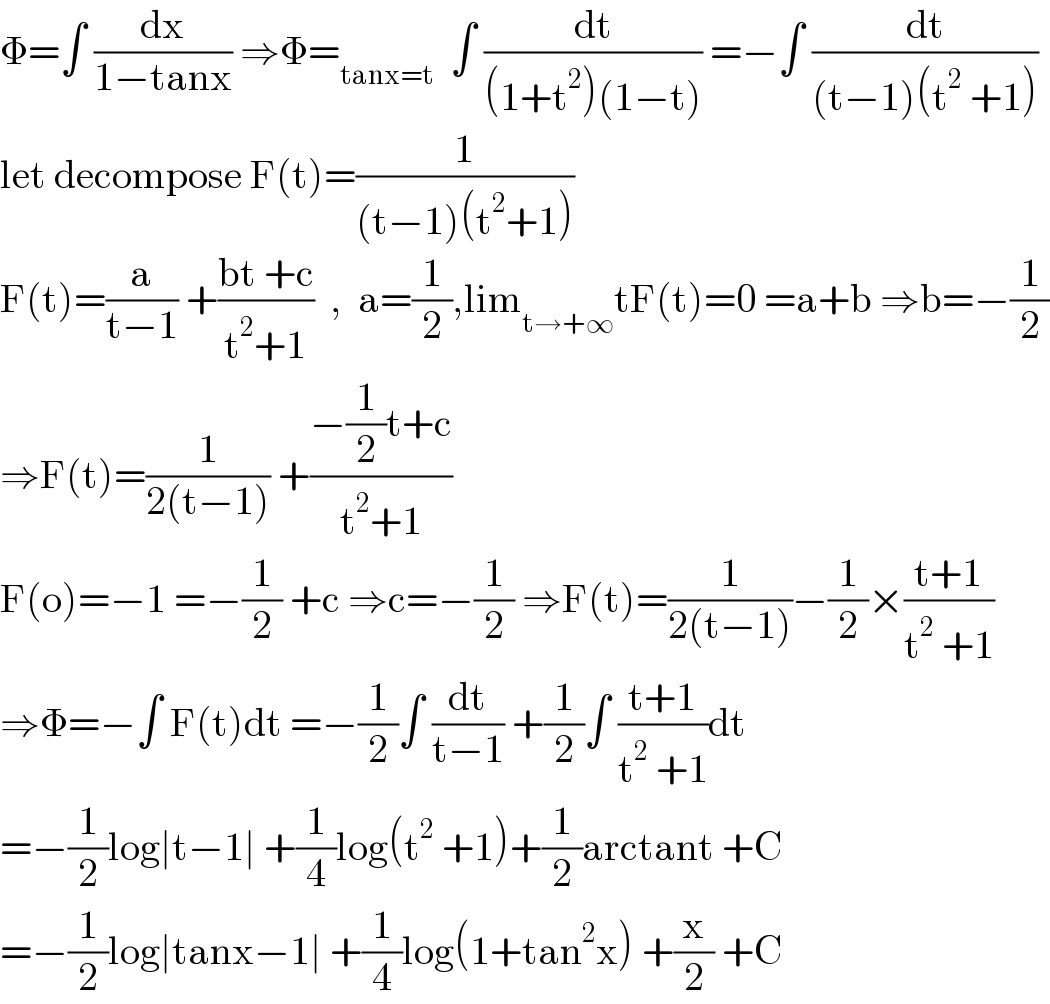
| ||
Question and Answers Forum | ||
Question Number 141805 by mohammad17 last updated on 23/May/21 | ||
 | ||
Answered by MJS_new last updated on 23/May/21 | ||
![∫(dx/(1−tan x))= [t=tan x → dx=(dt/(t^2 +1))] =∫(dt/((1−t)(t^2 +1)))= =(1/4)∫((2t)/(t^2 +1))dt+(1/2)∫(dt/(t^2 +1))−(1/2)∫(dt/(t−1))= =(1/4)ln (t^2 +1) +(1/2)arctan t −(1/2)ln (t−1) = =(1/4)ln ((t^2 +1)/((t−1)^2 )) +(1/2)arctan t = =(x/2)−(1/4)ln (1−sin 2x) +C](Q141809.png) | ||
| ||
Answered by mathmax by abdo last updated on 24/May/21 | ||
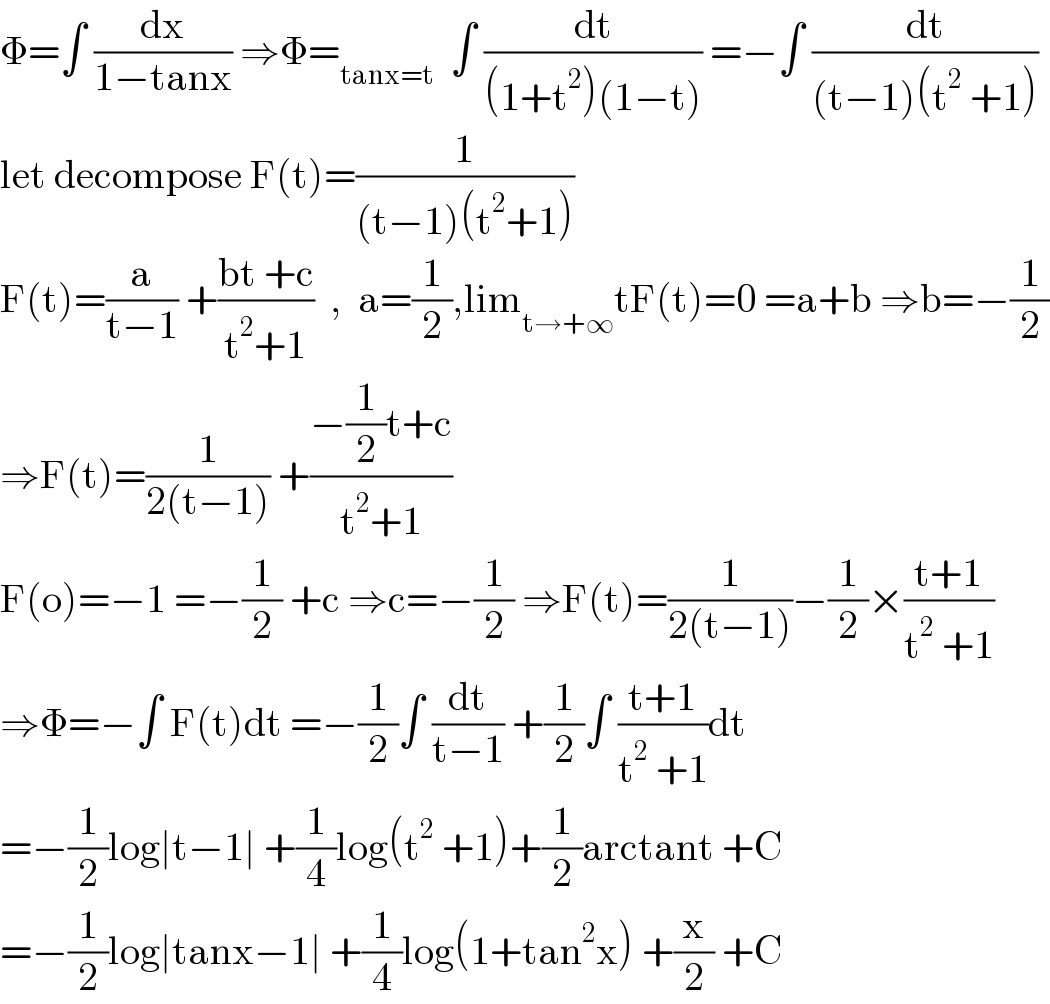 | ||
| ||