
Question and Answers Forum
Question Number 141811 by mnjuly1970 last updated on 23/May/21
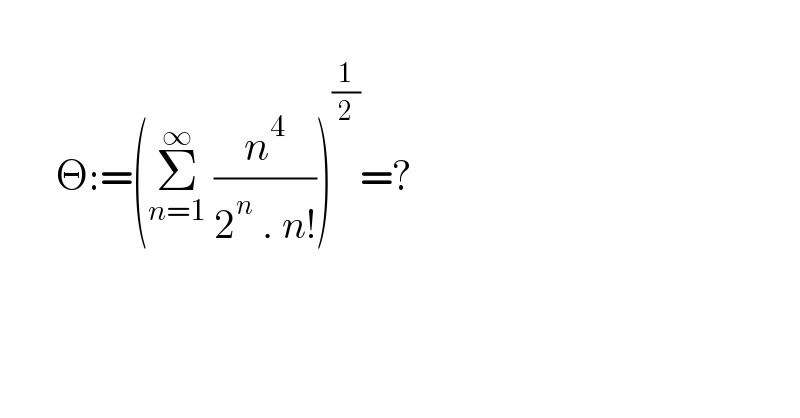
Answered by qaz last updated on 23/May/21
![(xD)^4 =xDxDxDxD =xDxDx(D+xD^2 ) =xDx[(D+xD^2 )+x(D^2 +D^2 +xD^3 ] =xDx(D+3xD^2 +x^2 D^3 ) =x[(D+3xD^2 +x^2 D^3 )+x(D^2 +3D^2 +3xD^3 +2xD^3 +x^2 D^4 )] =xD+7x^2 D^2 +6x^3 D^3 +x^4 D^4 Θ=(Σ_(n=1) ^∞ (n^4 /(2^n n!)))^2 =((xD)^4 (Σ_(n=0) ^∞ (x^n /(n!))−1))^(1/2) ∣_(x=1/2) =[(xD)^4 (e^x −1)]^(1/2) ∣_(x=1/2) =[(x+7x^2 +6x^3 +x^4 )e^x ]^(1/2) ∣_(x=1/2) =((1/2)+(7/4)+(6/8)+(1/(16)))^(1/2) (e)^(1/4) =(7/4)(e)^(1/4)](Q141837.png)
Commented by mnjuly1970 last updated on 23/May/21
| ||
Question and Answers Forum | ||
Question Number 141811 by mnjuly1970 last updated on 23/May/21 | ||
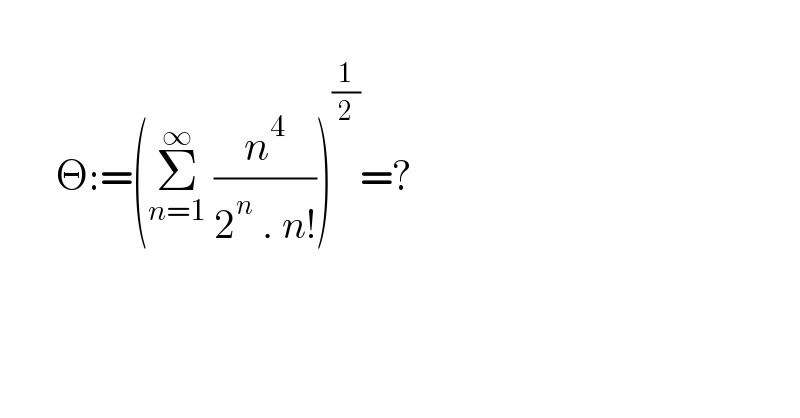 | ||
Answered by qaz last updated on 23/May/21 | ||
![(xD)^4 =xDxDxDxD =xDxDx(D+xD^2 ) =xDx[(D+xD^2 )+x(D^2 +D^2 +xD^3 ] =xDx(D+3xD^2 +x^2 D^3 ) =x[(D+3xD^2 +x^2 D^3 )+x(D^2 +3D^2 +3xD^3 +2xD^3 +x^2 D^4 )] =xD+7x^2 D^2 +6x^3 D^3 +x^4 D^4 Θ=(Σ_(n=1) ^∞ (n^4 /(2^n n!)))^2 =((xD)^4 (Σ_(n=0) ^∞ (x^n /(n!))−1))^(1/2) ∣_(x=1/2) =[(xD)^4 (e^x −1)]^(1/2) ∣_(x=1/2) =[(x+7x^2 +6x^3 +x^4 )e^x ]^(1/2) ∣_(x=1/2) =((1/2)+(7/4)+(6/8)+(1/(16)))^(1/2) (e)^(1/4) =(7/4)(e)^(1/4)](Q141837.png) | ||
| ||
Commented by mnjuly1970 last updated on 23/May/21 | ||
 | ||