Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 141812 by mathsuji last updated on 23/May/21

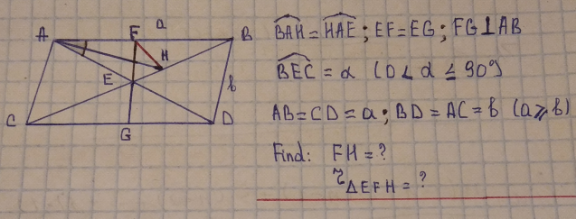
Commented by mr W last updated on 23/May/21

$$checkyourquestionanddiagram!$$$$\mathrm{\angle }BEC=\alpha ?$$$$butaccordingtodiagram$$$$\mathrm{\angle }BEC=180°$$

Commented by mathsuji last updated on 23/May/21

$$Sorrysir,BED=\alpha$$

Answered by mr W last updated on 24/May/21

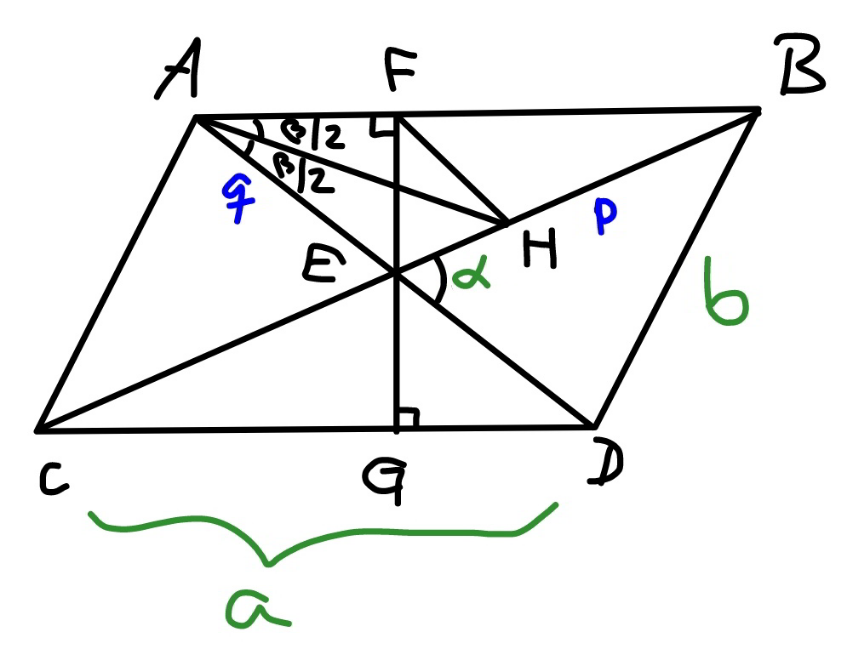
Commented by mr W last updated on 24/May/21

$$given:a,b,\alpha$$$$letp=EB,q=EA,\mathrm{\angle }EAB=\beta$$$$b^2=p^2+q^2-2pq\cos \alpha$$$$a^2=p^2+q^2+2pq\cos \alpha$$$$if\alpha =90°:p=q=\frac{\sqrt{a^2+b^2}}{2}$$$$otherwise:$$$$\Rightarrow pq=\frac{a^2-b^2}{4\cos \alpha }=\mu ,say$$$$\Rightarrow p^2+q^2=\frac{a^2+b^2}{2}=\lambda ,say$$$$\Rightarrow p^4+q^2{p}^2=\lambda p^2$$$$\Rightarrow p^4-\lambda p^2+{\mu }^2=0$$$$\Rightarrow p^2=\frac{\lambda \pm \sqrt{{\lambda }^2-4{\mu }^2}}{2}$$$$\Rightarrow p=\sqrt{\frac{\lambda +\sqrt{{\lambda }^2-4{\mu }^2}}{2}}$$$$\Rightarrow q=\sqrt{\frac{\lambda -\sqrt{{\lambda }^2-4{\mu }^2}}{2}}$$$$\frac{\sin \beta }{p}=\frac{\sin \alpha }{a}$$$$\Rightarrow \sin \beta =\frac{p\sin \alpha }{a}$$$$\Rightarrow \beta ={\sin }^{-1}\left(\frac{p\sin \alpha }{a}\right)$$$$EF=q\sin \beta =\frac{pq\sin \alpha }{a}=\frac{(a^2-b^2)\tan \alpha }{4a}$$$$\frac{EH}{\sin \frac{\beta }{2}}=\frac{q}{\sin \alpha }$$$$\Rightarrow EH=\frac{q\sin \frac{\beta }{2}}{\sin \alpha }$$$$A_{\mathrm{\Delta }EFH}=\frac{EF\times EH\times \sin (\frac{\pi }{2}-\alpha +\beta )}{2}$$$$\Rightarrow A_{\mathrm{\Delta }EFH}=\frac{(a^2-b^2)q\sin \frac{\beta }{2}\cos (\alpha -\beta )}{8a\cos \alpha }$$$${FH}^2={EF}^2+{EH}^2-2\times EF\times EH\times \cos (\frac{\pi }{2}-\alpha +\beta )$$$$\Rightarrow EH=\sqrt{{\left[\frac{(a^2-b^2)\tan \alpha }{4a}\right]}^2+{\left[\frac{q\sin \frac{\beta }{2}}{\sin \alpha }\right]}^2-\frac{(a^2-b^2)q\sin \frac{\beta }{2}\sin (\alpha -\beta )}{2a\cos \alpha }}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com