
Question and Answers Forum
Question Number 141847 by iloveisrael last updated on 24/May/21
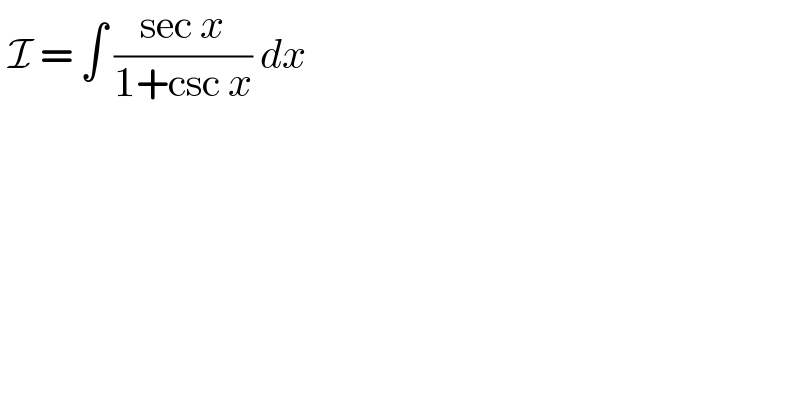
Answered by MJS_new last updated on 24/May/21
![∫((sec x)/(1+csc x))= [t=tan (x/2) → dx=2cos^2 (x/2) dt] =−4∫(t/((t−1)(t+1)^3 ))dt= =−(1/2)∫(dt/(t−1))−2∫(dt/((t+1)^3 ))+∫(dt/((t+1)^2 ))+(1/2)∫(dt/(t+1))= =−(1/2)ln (t−1) +(1/((t+1)^2 ))−(1/(t+1))+(1/2)ln (t+1) = =−(t/((t+1)^2 ))+(1/2)ln ((t+1)/(t−1)) =... =−((sin x)/(2(1+sin x)))+(1/2)ln ∣((cos x)/(1−sin x))∣ +C](Q141882.png)
Answered by iloveisrael last updated on 24/May/21
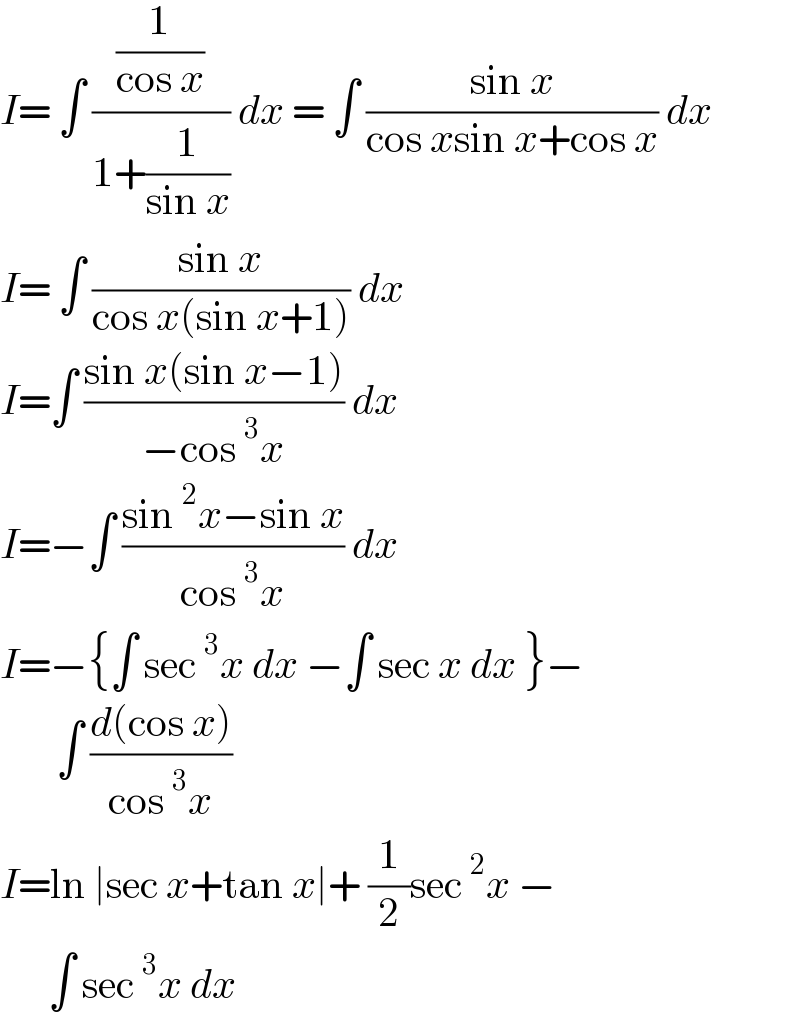
| ||
Question and Answers Forum | ||
Question Number 141847 by iloveisrael last updated on 24/May/21 | ||
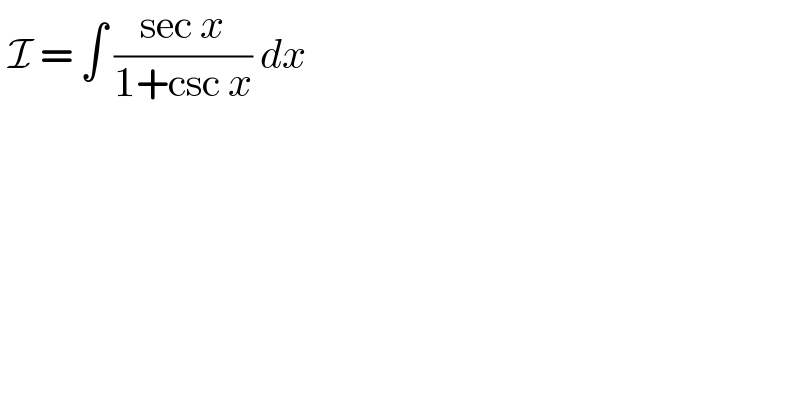 | ||
Answered by MJS_new last updated on 24/May/21 | ||
![∫((sec x)/(1+csc x))= [t=tan (x/2) → dx=2cos^2 (x/2) dt] =−4∫(t/((t−1)(t+1)^3 ))dt= =−(1/2)∫(dt/(t−1))−2∫(dt/((t+1)^3 ))+∫(dt/((t+1)^2 ))+(1/2)∫(dt/(t+1))= =−(1/2)ln (t−1) +(1/((t+1)^2 ))−(1/(t+1))+(1/2)ln (t+1) = =−(t/((t+1)^2 ))+(1/2)ln ((t+1)/(t−1)) =... =−((sin x)/(2(1+sin x)))+(1/2)ln ∣((cos x)/(1−sin x))∣ +C](Q141882.png) | ||
| ||
Answered by iloveisrael last updated on 24/May/21 | ||
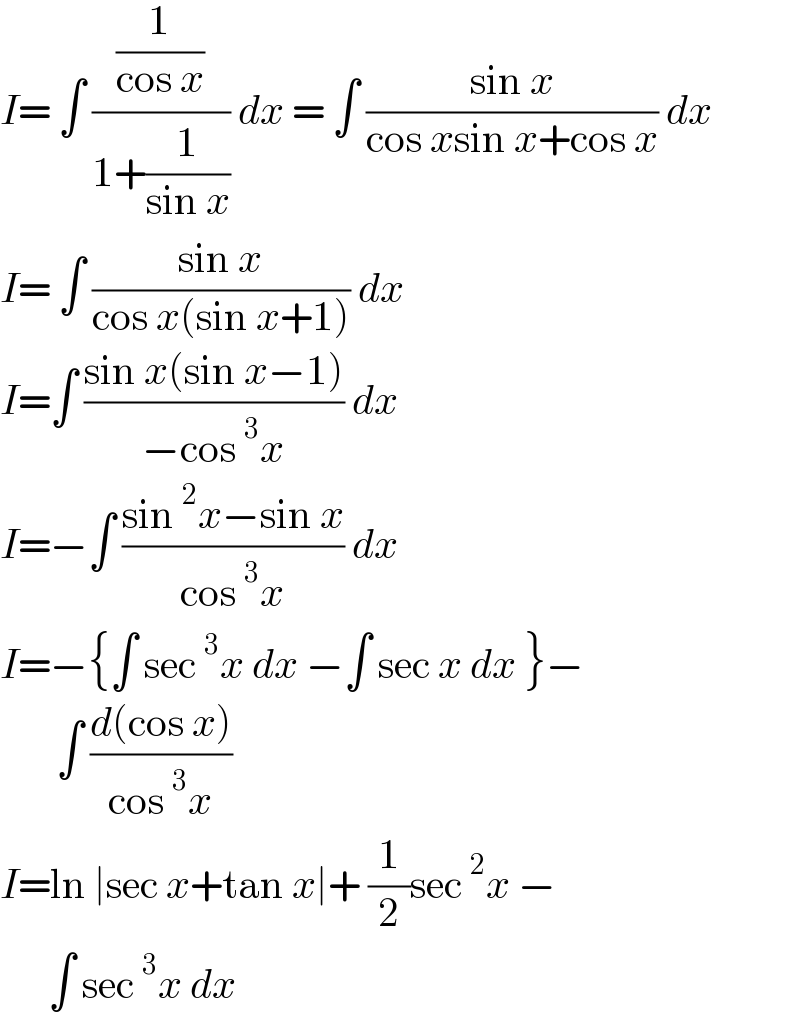 | ||
| ||