
Question and Answers Forum
Question Number 141916 by mnjuly1970 last updated on 24/May/21
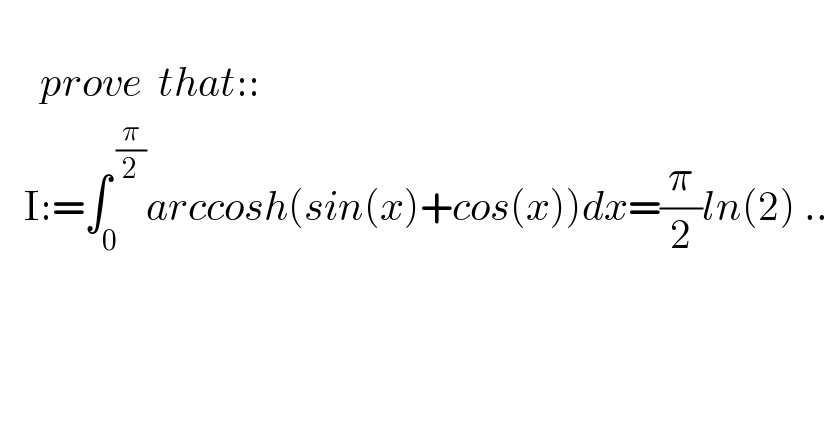
Answered by mindispower last updated on 25/May/21
![by part withe d(arccoh(x))=(dx/( (√(1−x^2 )))) I=xarccosh(sinx+cos(x))]_0 ^(π/2) −∫_0 ^(π/2) ((x(cos(x)−sin(x)))/( (√(sin(2x)))))dx −∫_0 ^(π/2) ((xcos(x)−xsin(x))/( (√(sin(2x)))))dx =−(1/( (√2)))∫_0 ^(π/2) xsin^(−(1/2)) (x)cos^(1/2) (x)+(1/( (√2)))∫_0 ^(π/2) xsin^(1/2) (x)cos^(−(1/2)) (x) (1/( (√2)))∫_0 ^∞ ((arctg(x)((√x)−(1/( (√x)))))/(1+x^2 ))dx=A ∫_0 ^∞ ((x^s arctan(tx))/(1+x^2 )) dx=f(t),s∈]−1,1[ f′(t)=∫_0 ^∞ (x^(s+1) /((1+x^2 )(1+t^2 x^2 )))dx ∫_(−∞) ^∞ (x^(s+1) /((1+x^2 )(1+t^2 x^2 )))dx=a=2iπ(.(i^(s+1) /(2i(1−t^2 )))+((i^(s+1) t^2 )/(t^(s+1) .(t^2 −1))).(1/(2it))) =((πi^(s+1) )/(1−t^2 ))(1−t^(−s) ) a=f(t)+∫_0 ^∞ (((−x)^(s+1) )/((1+x^2 )(1+t^2 x^2 )))dx =(1+(−1)^(s+1) )f(t) =(1+e^(iπ(s+1)) )f(t) f(t)=(π/(1−t^2 ))(1−t^(−s) ).(e^(i(π/2)(s+1)) /(1+e^(iπ(s+1)) )) =((π(1−t^(−s) ))/(2(1−t^2 )cos((π/2)(s+1))))=f′(t) ∫_0 ^1 f′(t)=((x^s arctan(x))/(1+x^2 )) =(π/(2cos((π/2)(s+1))))∫_0 ^1 ((1−t^(−s) )/(1−t^2 ))dt_(t^2 =x) =−(π/(4sin(((πs)/2))))∫_0 ^1 ((1−x^(−(s/2)) )/(1−x))x^(−(1/2)) =−(π/(4sin(((πs)/2))))∫_0 ^1 ((x^(−(1/2)) −x^(−((s+1)/2)) )/(1−x))dx=g(s) Ψ(s+1)=−γ+∫_0 ^1 ((1−x^s )/(1−x))dx g(s)=−(π/(4sin(((πs)/2)))).(Ψ(((1−s)/2))−Ψ((1/2))) A=−(π/(4sin((π/4))(√2)))(Ψ((1/4))−2Ψ((1/2))+Ψ((3/4))) Ψ((1/2))=−2ln(2)−γ Ψ((1/4))=(−(π/2)−3ln(2)−γ) Ψ((3/4))=Ψ((1/4))+π =−(π/4)(−π−6ln(2)−2γ+π+4ln(2)+2γ) =−(π/4).−2ln(2)=(π/2)ln(2)](Q141960.png)
Commented by mnjuly1970 last updated on 25/May/21
Commented by mindispower last updated on 25/May/21

| ||
Question and Answers Forum | ||
Question Number 141916 by mnjuly1970 last updated on 24/May/21 | ||
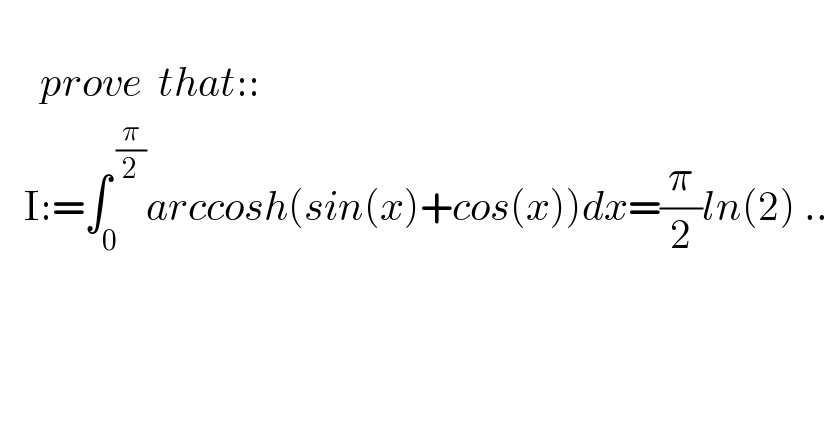 | ||
Answered by mindispower last updated on 25/May/21 | ||
![by part withe d(arccoh(x))=(dx/( (√(1−x^2 )))) I=xarccosh(sinx+cos(x))]_0 ^(π/2) −∫_0 ^(π/2) ((x(cos(x)−sin(x)))/( (√(sin(2x)))))dx −∫_0 ^(π/2) ((xcos(x)−xsin(x))/( (√(sin(2x)))))dx =−(1/( (√2)))∫_0 ^(π/2) xsin^(−(1/2)) (x)cos^(1/2) (x)+(1/( (√2)))∫_0 ^(π/2) xsin^(1/2) (x)cos^(−(1/2)) (x) (1/( (√2)))∫_0 ^∞ ((arctg(x)((√x)−(1/( (√x)))))/(1+x^2 ))dx=A ∫_0 ^∞ ((x^s arctan(tx))/(1+x^2 )) dx=f(t),s∈]−1,1[ f′(t)=∫_0 ^∞ (x^(s+1) /((1+x^2 )(1+t^2 x^2 )))dx ∫_(−∞) ^∞ (x^(s+1) /((1+x^2 )(1+t^2 x^2 )))dx=a=2iπ(.(i^(s+1) /(2i(1−t^2 )))+((i^(s+1) t^2 )/(t^(s+1) .(t^2 −1))).(1/(2it))) =((πi^(s+1) )/(1−t^2 ))(1−t^(−s) ) a=f(t)+∫_0 ^∞ (((−x)^(s+1) )/((1+x^2 )(1+t^2 x^2 )))dx =(1+(−1)^(s+1) )f(t) =(1+e^(iπ(s+1)) )f(t) f(t)=(π/(1−t^2 ))(1−t^(−s) ).(e^(i(π/2)(s+1)) /(1+e^(iπ(s+1)) )) =((π(1−t^(−s) ))/(2(1−t^2 )cos((π/2)(s+1))))=f′(t) ∫_0 ^1 f′(t)=((x^s arctan(x))/(1+x^2 )) =(π/(2cos((π/2)(s+1))))∫_0 ^1 ((1−t^(−s) )/(1−t^2 ))dt_(t^2 =x) =−(π/(4sin(((πs)/2))))∫_0 ^1 ((1−x^(−(s/2)) )/(1−x))x^(−(1/2)) =−(π/(4sin(((πs)/2))))∫_0 ^1 ((x^(−(1/2)) −x^(−((s+1)/2)) )/(1−x))dx=g(s) Ψ(s+1)=−γ+∫_0 ^1 ((1−x^s )/(1−x))dx g(s)=−(π/(4sin(((πs)/2)))).(Ψ(((1−s)/2))−Ψ((1/2))) A=−(π/(4sin((π/4))(√2)))(Ψ((1/4))−2Ψ((1/2))+Ψ((3/4))) Ψ((1/2))=−2ln(2)−γ Ψ((1/4))=(−(π/2)−3ln(2)−γ) Ψ((3/4))=Ψ((1/4))+π =−(π/4)(−π−6ln(2)−2γ+π+4ln(2)+2γ) =−(π/4).−2ln(2)=(π/2)ln(2)](Q141960.png) | ||
| ||
Commented by mnjuly1970 last updated on 25/May/21 | ||
 | ||
Commented by mindispower last updated on 25/May/21 | ||
 | ||