
Question and Answers Forum
Question Number 141931 by mathmax by abdo last updated on 24/May/21
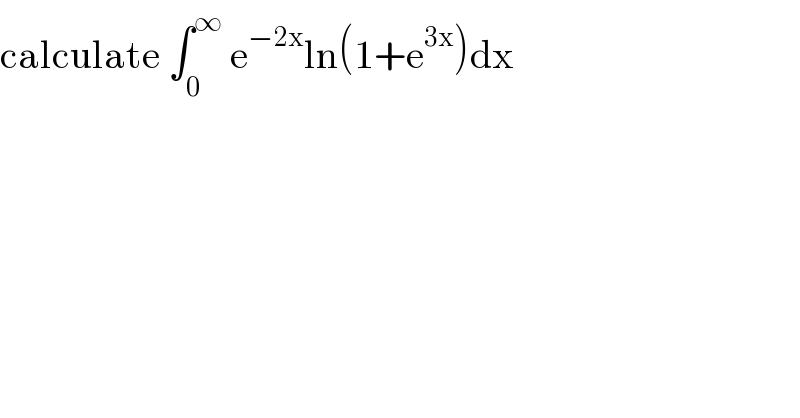
Answered by mindispower last updated on 24/May/21
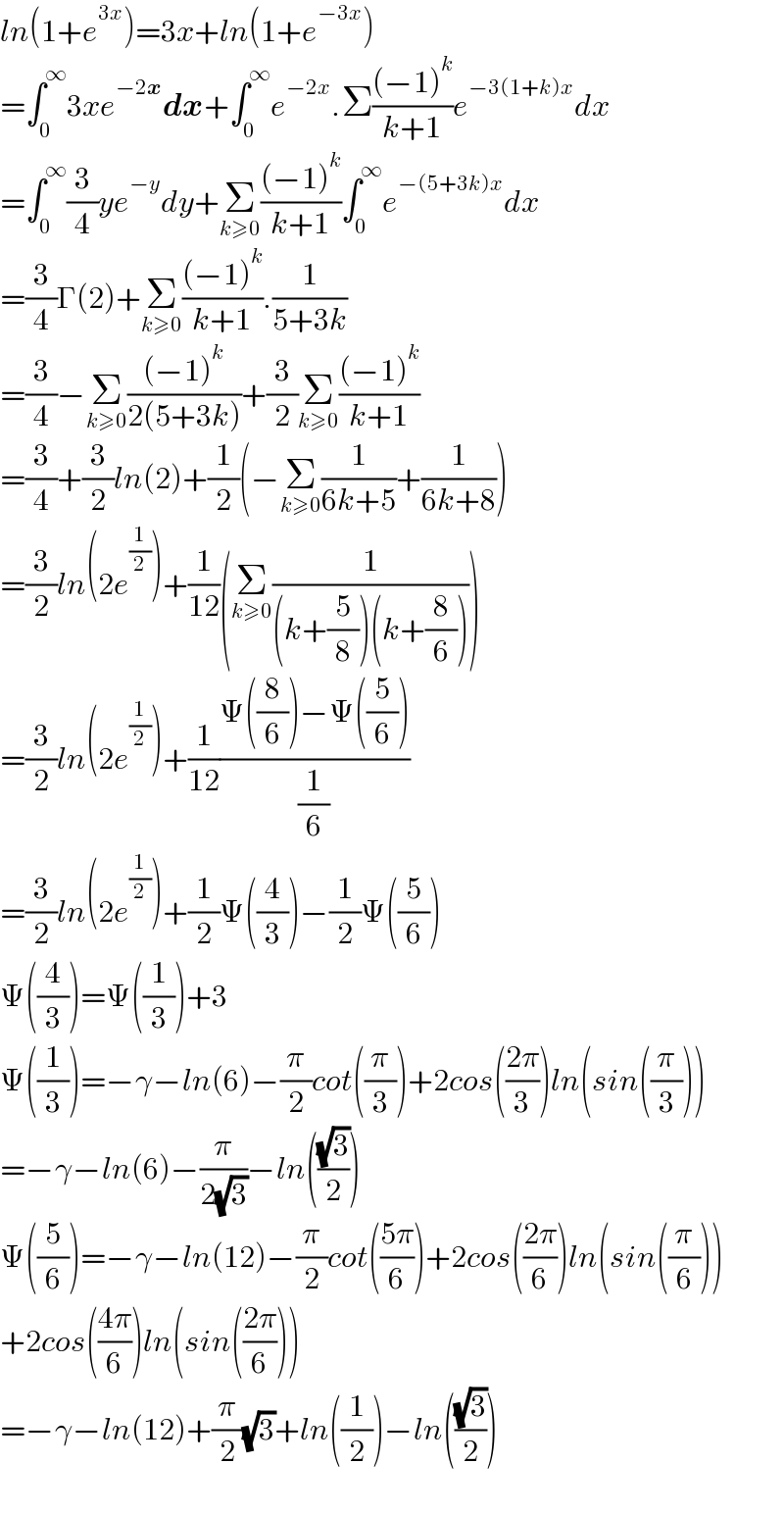
Commented by Mathspace last updated on 24/May/21

Answered by mathmax by abdo last updated on 26/May/21
![Φ=∫_0 ^∞ e^(−2x) log(1+e^(3x) )dx by parts Φ=[−(1/2)e^(−2x) log(1+e^(3x) )]_0 ^∞ +(1/2)∫_0 ^∞ e^(−2x) ×((3e^(3x) )/(1+e^(3x) ))dx =((log2)/2) +(3/2)∫_0 ^∞ (e^x /(1+e^(3x) ))dx but ∫_0 ^∞ (e^x /(1+e^(3x) ))dx =_(e^x =t) ∫_0 ^∞ (t/(1+t^3 ))×(dt/t)=∫_1 ^∞ (dt/(t^3 +1)) F(t)=(1/(t^3 +1))=(1/((t+1)(t^2 −t +1)))=(a/(t+1))+((bt +c)/(t^2 −t+1)) a=(1/3),lim_(t→+∞) tF(t)=0 =a+b ⇒b=−(1/3) F(0)=1=a+c ⇒c=1−(1/3)=(2/3) ⇒ F(t)=(1/(3(t+1)))+((−(1/3)t+(2/3))/(t^2 −t+1))=(1/(3(t+1)))−(1/3)((t−2)/(t^2 −t +1)) ⇒ ∫_1 ^∞ F(t)dt =[(1/3)log∣((t+1)/( (√(t^2 −t+1))))∣]_1 ^∞ (→0) +(2/3)∫_1 ^∞ (dt/(t^2 −t +1)) ∫_1 ^∞ (dt/(t^2 −t +1))=∫_1 ^∞ (dt/((t−(1/2))^2 +(3/4)))=_(t−(1/2)=((√3)/2)y →y=((2t−1)/( (√3)))) =(4/3)∫_(1/( (√3))) ^∞ (1/(y^2 +1))((√3)/2)dy =(2/( (√3)))[arctany]_(1/( (√3))) ^∞ =(2/( (√3)))((π/2)−(π/6))=(2/( (√3))).(π/3) =((2π)/(3(√3))) ⇒Φ=((log2)/2)+(3/2).((2π)/(3(√3))) ⇒Φ=((log2)/2) +(π/( (√3)))](Q142074.png)
| ||
Question and Answers Forum | ||
Question Number 141931 by mathmax by abdo last updated on 24/May/21 | ||
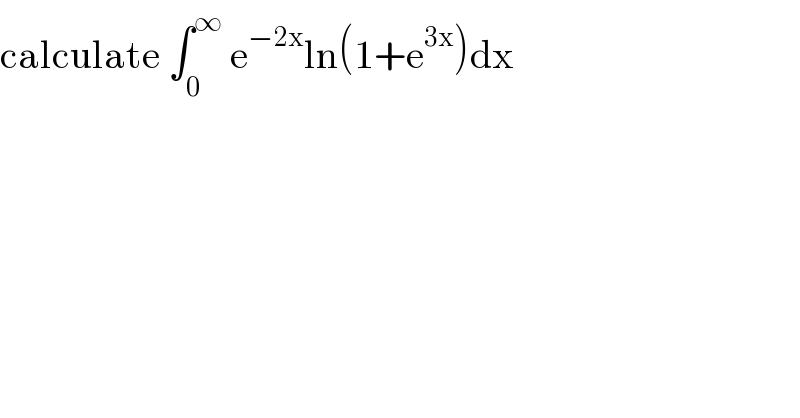 | ||
Answered by mindispower last updated on 24/May/21 | ||
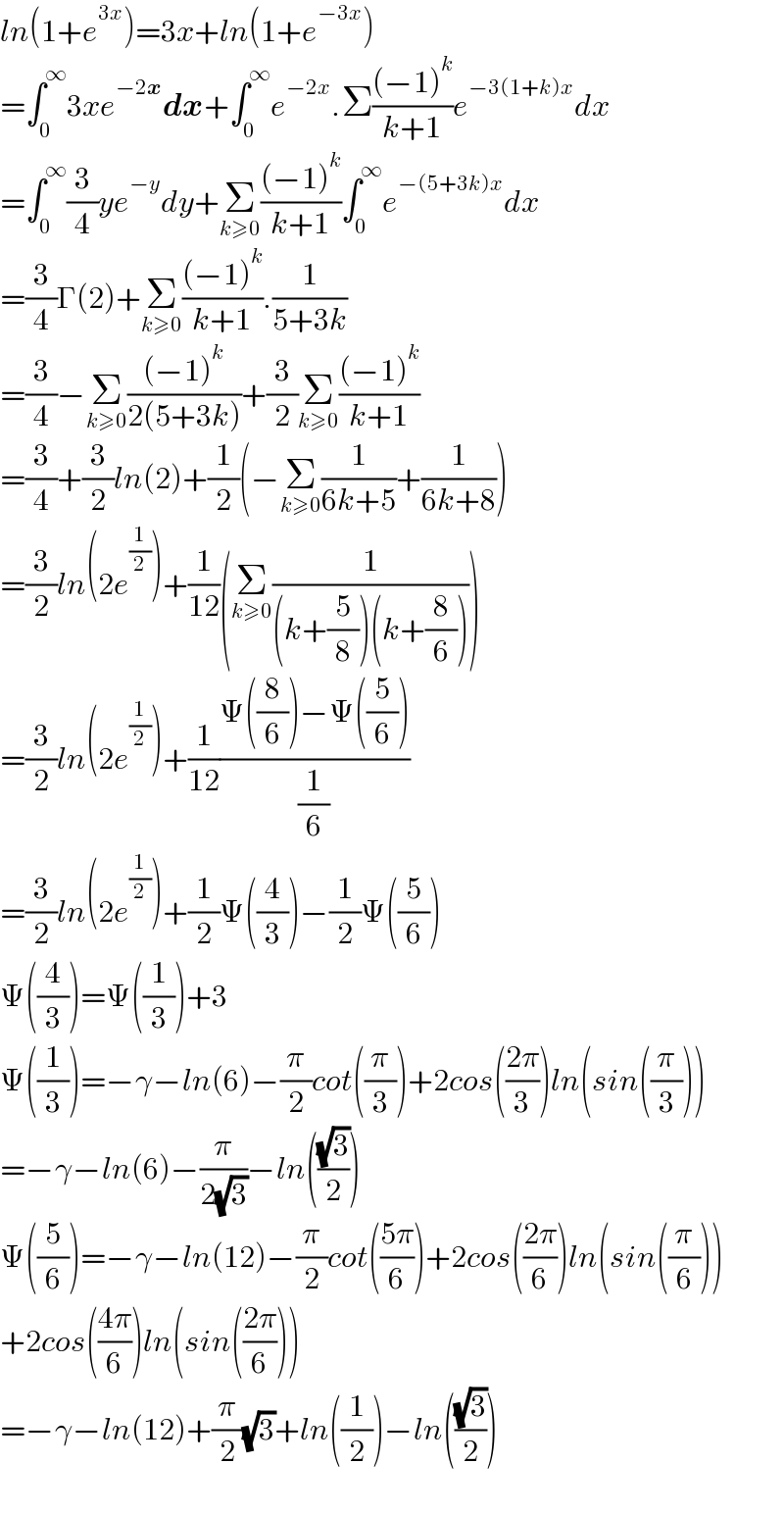 | ||
| ||
Commented by Mathspace last updated on 24/May/21 | ||
 | ||
Answered by mathmax by abdo last updated on 26/May/21 | ||
![Φ=∫_0 ^∞ e^(−2x) log(1+e^(3x) )dx by parts Φ=[−(1/2)e^(−2x) log(1+e^(3x) )]_0 ^∞ +(1/2)∫_0 ^∞ e^(−2x) ×((3e^(3x) )/(1+e^(3x) ))dx =((log2)/2) +(3/2)∫_0 ^∞ (e^x /(1+e^(3x) ))dx but ∫_0 ^∞ (e^x /(1+e^(3x) ))dx =_(e^x =t) ∫_0 ^∞ (t/(1+t^3 ))×(dt/t)=∫_1 ^∞ (dt/(t^3 +1)) F(t)=(1/(t^3 +1))=(1/((t+1)(t^2 −t +1)))=(a/(t+1))+((bt +c)/(t^2 −t+1)) a=(1/3),lim_(t→+∞) tF(t)=0 =a+b ⇒b=−(1/3) F(0)=1=a+c ⇒c=1−(1/3)=(2/3) ⇒ F(t)=(1/(3(t+1)))+((−(1/3)t+(2/3))/(t^2 −t+1))=(1/(3(t+1)))−(1/3)((t−2)/(t^2 −t +1)) ⇒ ∫_1 ^∞ F(t)dt =[(1/3)log∣((t+1)/( (√(t^2 −t+1))))∣]_1 ^∞ (→0) +(2/3)∫_1 ^∞ (dt/(t^2 −t +1)) ∫_1 ^∞ (dt/(t^2 −t +1))=∫_1 ^∞ (dt/((t−(1/2))^2 +(3/4)))=_(t−(1/2)=((√3)/2)y →y=((2t−1)/( (√3)))) =(4/3)∫_(1/( (√3))) ^∞ (1/(y^2 +1))((√3)/2)dy =(2/( (√3)))[arctany]_(1/( (√3))) ^∞ =(2/( (√3)))((π/2)−(π/6))=(2/( (√3))).(π/3) =((2π)/(3(√3))) ⇒Φ=((log2)/2)+(3/2).((2π)/(3(√3))) ⇒Φ=((log2)/2) +(π/( (√3)))](Q142074.png) | ||
| ||