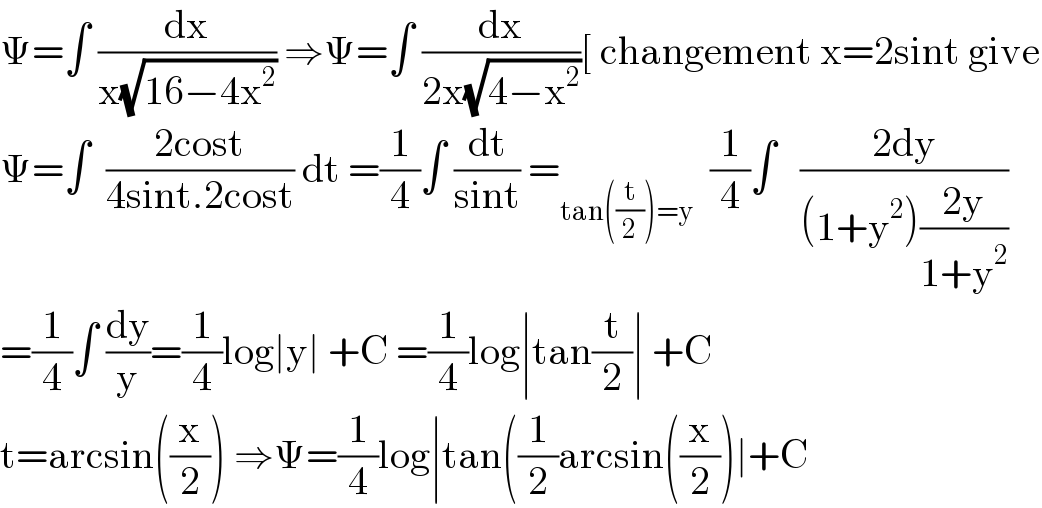Question Number 141943 by cesarL last updated on 25/May/21
$$\int\frac{{dx}}{{x}\sqrt{\mathrm{16}−\mathrm{4}{x}^{\mathrm{2}} }} \\ $$
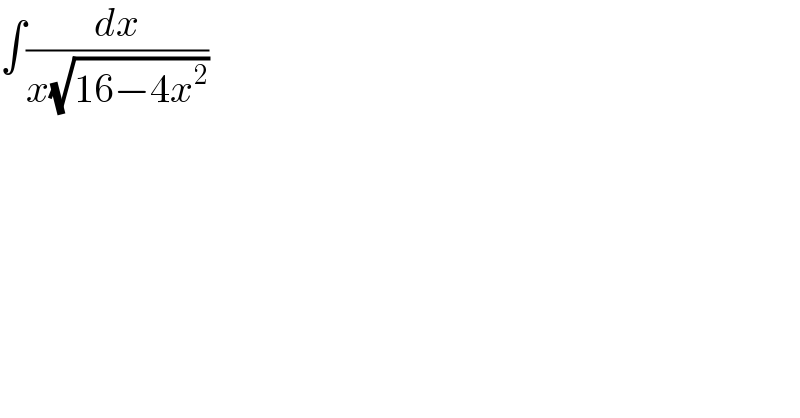
Answered by MJS_new last updated on 25/May/21
![∫(dx/(x(√(16−4x^2 ))))=(1/2)∫(dx/(x(√(4−x^2 ))))= [t=((2+(√(4−x^2 )))/x) → dx=−((x^2 (√(4−x^2 )))/(2(2+(√(4−x^2 )))))dt] =−(1/4)∫(dt/t)=−(1/4)ln t = =(1/4)ln ∣x∣ −(1/4)ln (2+(√(4−x^2 ))) +C](Q141951.png)
$$\int\frac{{dx}}{{x}\sqrt{\mathrm{16}−\mathrm{4}{x}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{2}+\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{{x}}\:\rightarrow\:{dx}=−\frac{{x}^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\right)}{dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{dt}}{{t}}=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:{t}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\mid{x}\mid\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\right)\:+{C} \\ $$
Commented by cesarL last updated on 25/May/21
$${I}\:{need}\:{with}\:{trigonometric}\:{sustitution} \\ $$
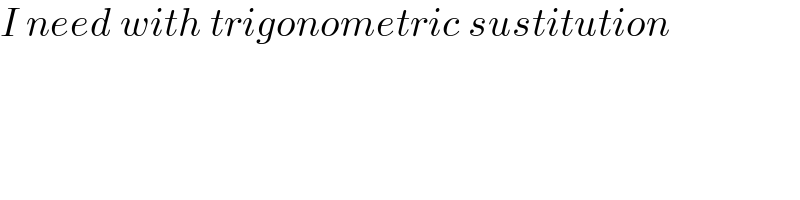
Commented by Ar Brandon last updated on 25/May/21
$$\mathrm{Then}\:\mathrm{you}\:\mathrm{may}\:\mathrm{let}\:\mathrm{x}=\mathrm{2sin}\theta \\ $$
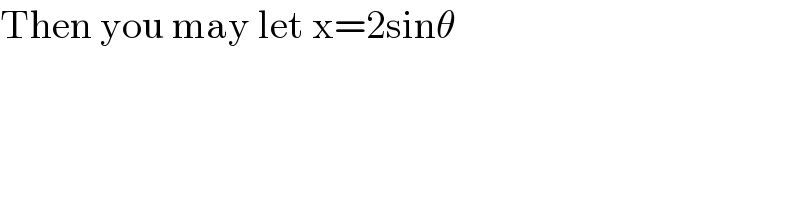
Answered by mathmax by abdo last updated on 25/May/21
$$\Psi=\int\:\frac{\mathrm{dx}}{\mathrm{x}\sqrt{\mathrm{16}−\mathrm{4x}^{\mathrm{2}} }}\:\Rightarrow\Psi=\int\:\frac{\mathrm{dx}}{\mathrm{2x}\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}\left[\:\mathrm{changement}\:\mathrm{x}=\mathrm{2sint}\:\mathrm{give}\right. \\ $$$$\Psi=\int\:\:\frac{\mathrm{2cost}}{\mathrm{4sint}.\mathrm{2cost}}\:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{dt}}{\mathrm{sint}}\:=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{y}} \:\:\frac{\mathrm{1}}{\mathrm{4}}\int\:\:\:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\frac{\mathrm{2y}}{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{dy}}{\mathrm{y}}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\mid\mathrm{y}\mid\:+\mathrm{C}\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\mid\mathrm{tan}\frac{\mathrm{t}}{\mathrm{2}}\mid\:+\mathrm{C} \\ $$$$\mathrm{t}=\mathrm{arcsin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:\Rightarrow\Psi=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{log}\mid\mathrm{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arcsin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mid+\mathrm{C}\right. \\ $$