Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 141944 by cesarL last updated on 25/May/21

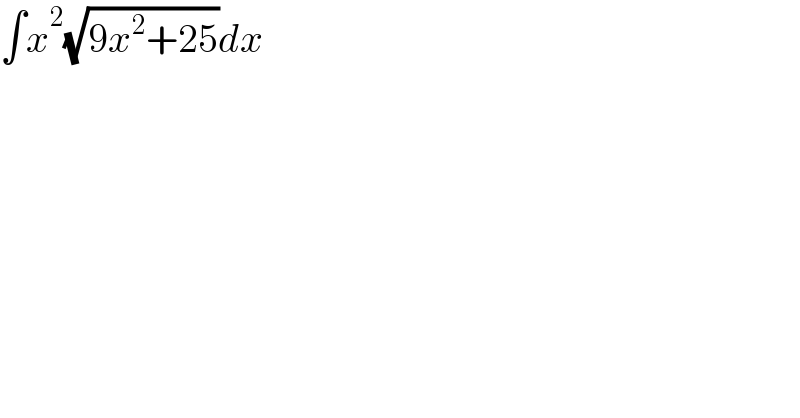
∫x^2 (√(9x^2 +25))dx

$$\int{x}^{\mathrm{2}} \sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}{dx} \\ $$

Answered by MJS_new last updated on 25/May/21

∫x^2 (√(9x^2 +25))dx= [t=((√(9x^2 +25))/x) → dx=−−((x^2 (√(9x^2 +25)))/(25))dt] =−625∫(t^2 /((t^2 −9)^3 ))dt= [Ostrogradski′s Method] =((625t(t^2 +9))/(72(t^2 −9)^2 ))+((625)/(72))∫(dt/(t^2 −9))= =((625t(t^2 +9))/(72(t^2 −9)^2 ))+((625)/(432))∫((1/(t−3))−(1/(t+3)))dt= =((625t(t^2 +9))/(72(t^2 −9)^2 ))+((625)/(432))ln ((t−3)/(t+3)) = =((x(18x^2 +25)(√(9x^2 +25)))/(72))−((625)/(216))ln (3x+(√(9x^2 +25))) +C

$$\int{x}^{\mathrm{2}} \sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}}{{x}}\:\rightarrow\:{dx}=−−\frac{{x}^{\mathrm{2}} \sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}}{\mathrm{25}}{dt}\right] \\ $$$$=−\mathrm{625}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{3}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{\mathrm{625}{t}\left({t}^{\mathrm{2}} +\mathrm{9}\right)}{\mathrm{72}\left({t}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{2}} }+\frac{\mathrm{625}}{\mathrm{72}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{9}}= \\ $$$$=\frac{\mathrm{625}{t}\left({t}^{\mathrm{2}} +\mathrm{9}\right)}{\mathrm{72}\left({t}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{2}} }+\frac{\mathrm{625}}{\mathrm{432}}\int\left(\frac{\mathrm{1}}{{t}−\mathrm{3}}−\frac{\mathrm{1}}{{t}+\mathrm{3}}\right){dt}= \\ $$$$=\frac{\mathrm{625}{t}\left({t}^{\mathrm{2}} +\mathrm{9}\right)}{\mathrm{72}\left({t}^{\mathrm{2}} −\mathrm{9}\right)^{\mathrm{2}} }+\frac{\mathrm{625}}{\mathrm{432}}\mathrm{ln}\:\frac{{t}−\mathrm{3}}{{t}+\mathrm{3}}\:= \\ $$$$=\frac{{x}\left(\mathrm{18}{x}^{\mathrm{2}} +\mathrm{25}\right)\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}}{\mathrm{72}}−\frac{\mathrm{625}}{\mathrm{216}}\mathrm{ln}\:\left(\mathrm{3}{x}+\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}\right)\:+{C} \\ $$

Answered by MJS_new last updated on 25/May/21

∫x^2 (√(9x^2 +25))dx= [u=((3x+(√(9x^2 +25)))/5) → dx=((5(√(9x^2 +25)))/(3(3x+(√(9x^2 +25)))))du] =((625)/(432))∫((u^8 −2u^4 +1)/u^5 )du=((625)/(432))∫(u^3 +(1/u^5 )−(2/u))du= =((625u^4 )/(1728))−((625)/(1728u^4 ))−((625)/(216))ln u = =((x(18x^2 +25)(√(9x^2 +25)))/(72))−((625)/(216))ln (3x+(√(9x^2 +25))) +C

$$\int{x}^{\mathrm{2}} \sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}{dx}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\mathrm{3}{x}+\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}}{\mathrm{5}}\:\rightarrow\:{dx}=\frac{\mathrm{5}\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}}{\mathrm{3}\left(\mathrm{3}{x}+\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}\right)}{du}\right] \\ $$$$=\frac{\mathrm{625}}{\mathrm{432}}\int\frac{{u}^{\mathrm{8}} −\mathrm{2}{u}^{\mathrm{4}} +\mathrm{1}}{{u}^{\mathrm{5}} }{du}=\frac{\mathrm{625}}{\mathrm{432}}\int\left({u}^{\mathrm{3}} +\frac{\mathrm{1}}{{u}^{\mathrm{5}} }−\frac{\mathrm{2}}{{u}}\right){du}= \\ $$$$=\frac{\mathrm{625}{u}^{\mathrm{4}} }{\mathrm{1728}}−\frac{\mathrm{625}}{\mathrm{1728}{u}^{\mathrm{4}} }−\frac{\mathrm{625}}{\mathrm{216}}\mathrm{ln}\:{u}\:= \\ $$$$=\frac{{x}\left(\mathrm{18}{x}^{\mathrm{2}} +\mathrm{25}\right)\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}}{\mathrm{72}}−\frac{\mathrm{625}}{\mathrm{216}}\mathrm{ln}\:\left(\mathrm{3}{x}+\sqrt{\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}}\right)\:+{C} \\ $$

Commented by cesarL last updated on 25/May/21

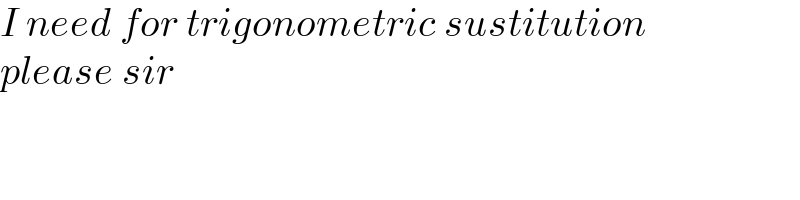
I need for trigonometric sustitution please sir

$${I}\:{need}\:{for}\:{trigonometric}\:{sustitution} \\ $$$${please}\:{sir} \\ $$

Answered by Ar Brandon last updated on 25/May/21

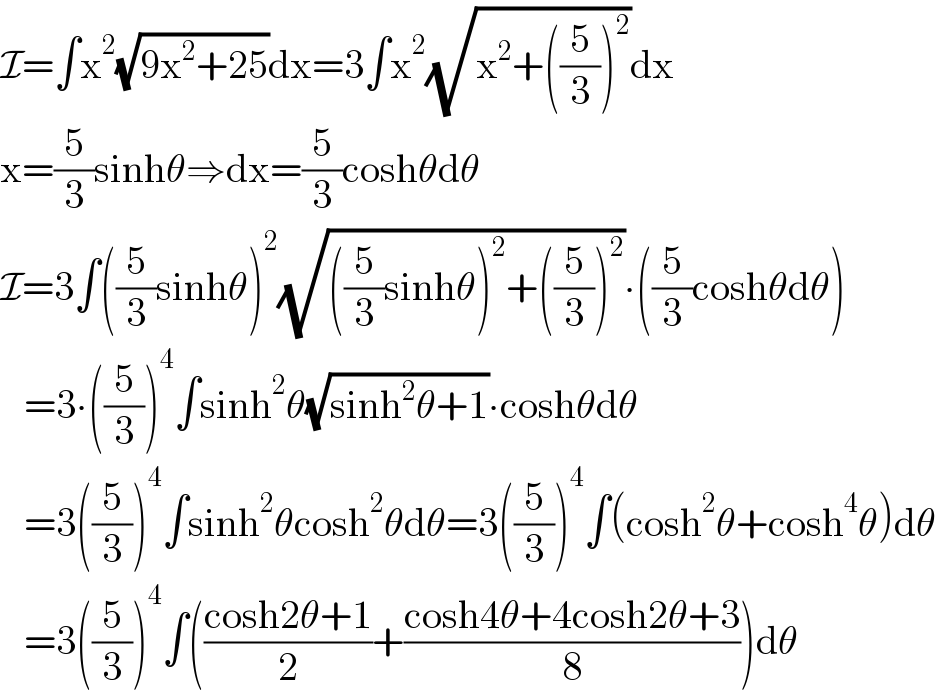
I=∫x^2 (√(9x^2 +25))dx=3∫x^2 (√(x^2 +((5/3))^2 ))dx x=(5/3)sinhθ⇒dx=(5/3)coshθdθ I=3∫((5/3)sinhθ)^2 (√(((5/3)sinhθ)^2 +((5/3))^2 ))∙((5/3)coshθdθ) =3∙((5/3))^4 ∫sinh^2 θ(√(sinh^2 θ+1))∙coshθdθ =3((5/3))^4 ∫sinh^2 θcosh^2 θdθ=3((5/3))^4 ∫(cosh^2 θ+cosh^4 θ)dθ =3((5/3))^4 ∫(((cosh2θ+1)/2)+((cosh4θ+4cosh2θ+3)/8))dθ

$$\mathcal{I}=\int\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{9x}^{\mathrm{2}} +\mathrm{25}}\mathrm{dx}=\mathrm{3}\int\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} +\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{x}=\frac{\mathrm{5}}{\mathrm{3}}\mathrm{sinh}\theta\Rightarrow\mathrm{dx}=\frac{\mathrm{5}}{\mathrm{3}}\mathrm{cosh}\theta\mathrm{d}\theta \\ $$$$\mathcal{I}=\mathrm{3}\int\left(\frac{\mathrm{5}}{\mathrm{3}}\mathrm{sinh}\theta\right)^{\mathrm{2}} \sqrt{\left(\frac{\mathrm{5}}{\mathrm{3}}\mathrm{sinh}\theta\right)^{\mathrm{2}} +\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{2}} }\centerdot\left(\frac{\mathrm{5}}{\mathrm{3}}\mathrm{cosh}\theta\mathrm{d}\theta\right) \\ $$$$\:\:\:=\mathrm{3}\centerdot\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{4}} \int\mathrm{sinh}^{\mathrm{2}} \theta\sqrt{\mathrm{sinh}^{\mathrm{2}} \theta+\mathrm{1}}\centerdot\mathrm{cosh}\theta\mathrm{d}\theta \\ $$$$\:\:\:=\mathrm{3}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{4}} \int\mathrm{sinh}^{\mathrm{2}} \theta\mathrm{cosh}^{\mathrm{2}} \theta\mathrm{d}\theta=\mathrm{3}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{4}} \int\left(\mathrm{cosh}^{\mathrm{2}} \theta+\mathrm{cosh}^{\mathrm{4}} \theta\right)\mathrm{d}\theta \\ $$$$\:\:\:=\mathrm{3}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{4}} \int\left(\frac{\mathrm{cosh2}\theta+\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{cosh4}\theta+\mathrm{4cosh2}\theta+\mathrm{3}}{\mathrm{8}}\right)\mathrm{d}\theta \\ $$

Commented by Ar Brandon last updated on 25/May/21

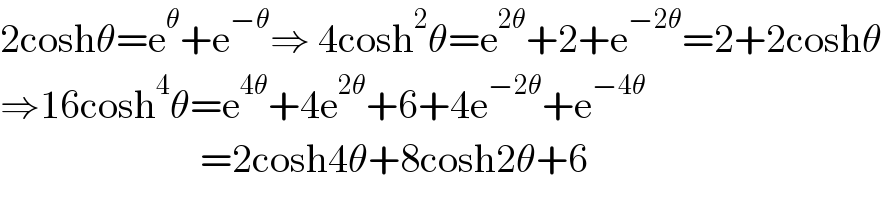
2coshθ=e^θ +e^(−θ) ⇒ 4cosh^2 θ=e^(2θ) +2+e^(−2θ) =2+2coshθ ⇒16cosh^4 θ=e^(4θ) +4e^(2θ) +6+4e^(−2θ) +e^(−4θ) =2cosh4θ+8cosh2θ+6

$$\mathrm{2cosh}\theta=\mathrm{e}^{\theta} +\mathrm{e}^{−\theta} \Rightarrow\:\mathrm{4cosh}^{\mathrm{2}} \theta=\mathrm{e}^{\mathrm{2}\theta} +\mathrm{2}+\mathrm{e}^{−\mathrm{2}\theta} =\mathrm{2}+\mathrm{2cosh}\theta \\ $$$$\Rightarrow\mathrm{16cosh}^{\mathrm{4}} \theta=\mathrm{e}^{\mathrm{4}\theta} +\mathrm{4e}^{\mathrm{2}\theta} +\mathrm{6}+\mathrm{4e}^{−\mathrm{2}\theta} +\mathrm{e}^{−\mathrm{4}\theta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2cosh4}\theta+\mathrm{8cosh2}\theta+\mathrm{6} \\ $$

Answered by mathmax by abdo last updated on 25/May/21

Φ=∫ x^2 (√(9x^2 +25))dx ⇒Φ=∫ 3x^2 (√(x^2 +((5/3))^2 ))dx =3f((5/3)) with f(a)=∫ x^2 (√(x^2 +a^2 ))dx changement x=ash(t)give f(a)=∫ a^2 sh^2 (t)ach(t)acht dt =a^4 ∫ sh^2 t ch^2 t dt =a^4 ∫((1/2)sh(2t))^2 dt =(a^4 /4)∫ sh^2 (2t)dt =(a^4 /8)∫(ch(4t)−1)dt =(a^4 /8)t −(a^4 /8)∫ ch(4t)dt =(a^4 /8)t−(a^4 /(64))sh(4t) +C [we[have sh(4t) =((e^(4t) +e^(−4t) )/2) and t=argsh((x/(a )))=log((x/a) +(√(1+(x^2 /a^2 )))) ⇒sh(4t)=(1/2){((x/a)+(√(1+(x^2 /a^2 ))))^4 +((x/a)+(√(1+(x^2 /a^2 ))))^(−4) } ⇒ f(a)=(a^4 /8)log((x/a)+(√(1+(x^2 /a^2 )))) −(a^4 /(128)){((x/a)+(√(1+(x^2 /a^2 ))))^4 +((x/a)+(√(1+(x^2 /a^2 ))))^(−4) } +C Φ=3f((5/3))

$$\Phi=\int\:\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{9x}^{\mathrm{2}} \:+\mathrm{25}}\mathrm{dx}\:\Rightarrow\Phi=\int\:\mathrm{3x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} \:+\left(\frac{\mathrm{5}}{\mathrm{3}}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{3f}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)\:\mathrm{with}\:\mathrm{f}\left(\mathrm{a}\right)=\int\:\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}=\mathrm{ash}\left(\mathrm{t}\right)\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int\:\mathrm{a}^{\mathrm{2}} \mathrm{sh}^{\mathrm{2}} \left(\mathrm{t}\right)\mathrm{ach}\left(\mathrm{t}\right)\mathrm{acht}\:\mathrm{dt}\:=\mathrm{a}^{\mathrm{4}} \int\:\mathrm{sh}^{\mathrm{2}} \mathrm{t}\:\mathrm{ch}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt} \\ $$$$=\mathrm{a}^{\mathrm{4}} \int\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sh}\left(\mathrm{2t}\right)\right)^{\mathrm{2}} \mathrm{dt}\:\:=\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{4}}\int\:\mathrm{sh}^{\mathrm{2}} \left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{8}}\int\left(\mathrm{ch}\left(\mathrm{4t}\right)−\mathrm{1}\right)\mathrm{dt}\:=\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{8}}\mathrm{t}\:−\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{8}}\int\:\mathrm{ch}\left(\mathrm{4t}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{8}}\mathrm{t}−\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{64}}\mathrm{sh}\left(\mathrm{4t}\right)\:+\mathrm{C}\:\left[\mathrm{we}\left[\mathrm{have}\right.\right. \\ $$$$\mathrm{sh}\left(\mathrm{4t}\right)\:=\frac{\mathrm{e}^{\mathrm{4t}} +\mathrm{e}^{−\mathrm{4t}} }{\mathrm{2}}\:\mathrm{and}\:\mathrm{t}=\mathrm{argsh}\left(\frac{\mathrm{x}}{\mathrm{a}\:}\right)=\mathrm{log}\left(\frac{\mathrm{x}}{\mathrm{a}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right) \\ $$$$\Rightarrow\mathrm{sh}\left(\mathrm{4t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\frac{\mathrm{x}}{\mathrm{a}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right)^{\mathrm{4}} \:+\left(\frac{\mathrm{x}}{\mathrm{a}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right)^{−\mathrm{4}} \right\}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{8}}\mathrm{log}\left(\frac{\mathrm{x}}{\mathrm{a}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right) \\ $$$$−\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{128}}\left\{\left(\frac{\mathrm{x}}{\mathrm{a}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right)^{\mathrm{4}} +\left(\frac{\mathrm{x}}{\mathrm{a}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right)^{−\mathrm{4}} \right\}\:+\mathrm{C} \\ $$$$\Phi=\mathrm{3f}\left(\frac{\mathrm{5}}{\mathrm{3}}\right) \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 25/May/21

sorry f(a)=−(a^4 /8)t+(a^4 /(64))sh(4t) +C ⇒ f(a)=−(a^4 /8)log((x/a)+(√(1+(x^2 /a^2 ))))+(a^4 /(128)){((x/a)+(√(1+(x^2 /a^2 ))))^4 +((x/a)+(√(1+(x^2 /a^2 ))))^(−4) }+C

$$\mathrm{sorry}\:\mathrm{f}\left(\mathrm{a}\right)=−\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{8}}\mathrm{t}+\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{64}}\mathrm{sh}\left(\mathrm{4t}\right)\:+\mathrm{C}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=−\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{8}}\mathrm{log}\left(\frac{\mathrm{x}}{\mathrm{a}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right)+\frac{\mathrm{a}^{\mathrm{4}} }{\mathrm{128}}\left\{\left(\frac{\mathrm{x}}{\mathrm{a}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right)^{\mathrm{4}} +\left(\frac{\mathrm{x}}{\mathrm{a}}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }}\right)^{−\mathrm{4}} \right\}+\mathrm{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com