
Question and Answers Forum
Question Number 142171 by iloveisrael last updated on 27/May/21
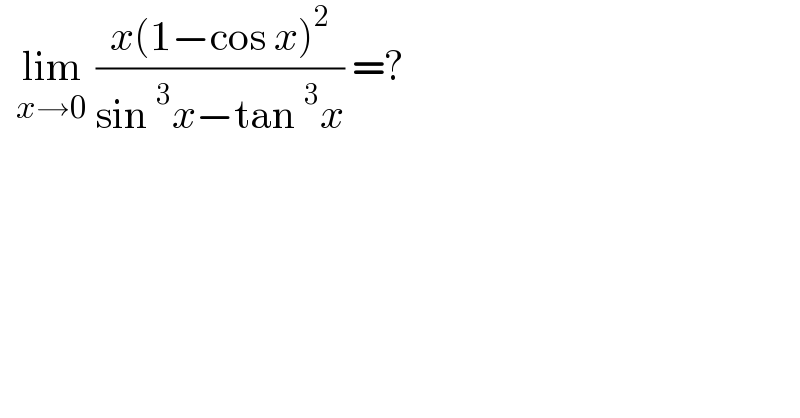
Answered by iloveisrael last updated on 27/May/21
![lim_(x→0) ((x(2sin^2 ((x/2)))^2 )/(tan^3 x(cos^3 x−1))) = lim_(x→0) ((4sin^4 ((x/2)))/(tan^2 x(−2sin^2 ((x/2)))(cos^2 x+cos x+1))) = (1/3).lim_(x→0) ((−2sin^2 ((x/2)))/(tan^2 x)) = (1/3). [−2((1/4))] = −(1/6).](Q142177.png)
Answered by liberty last updated on 27/May/21
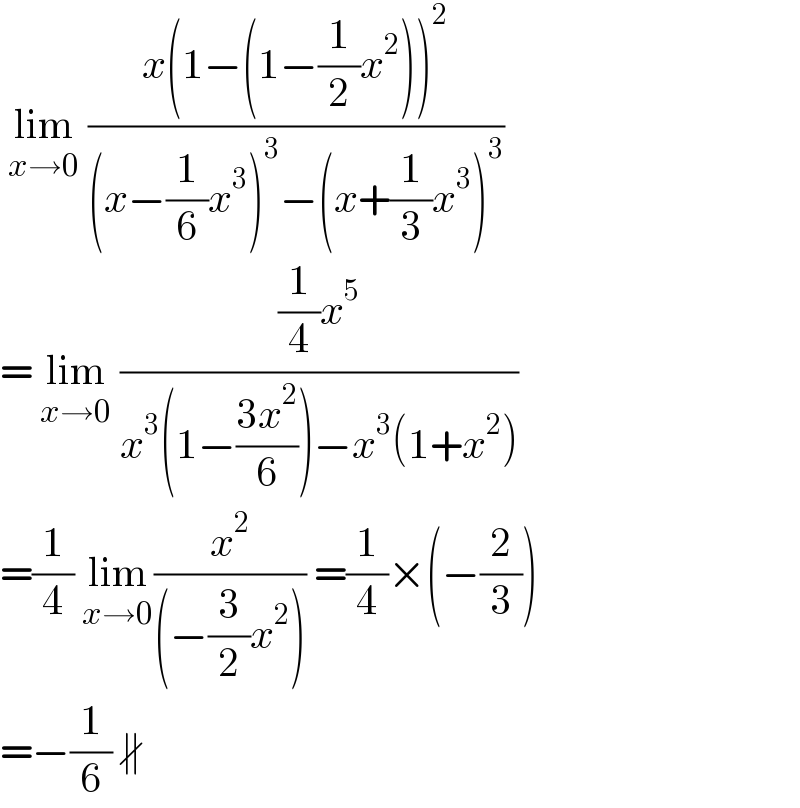
Answered by som(math1967) last updated on 27/May/21

| ||
Question and Answers Forum | ||
Question Number 142171 by iloveisrael last updated on 27/May/21 | ||
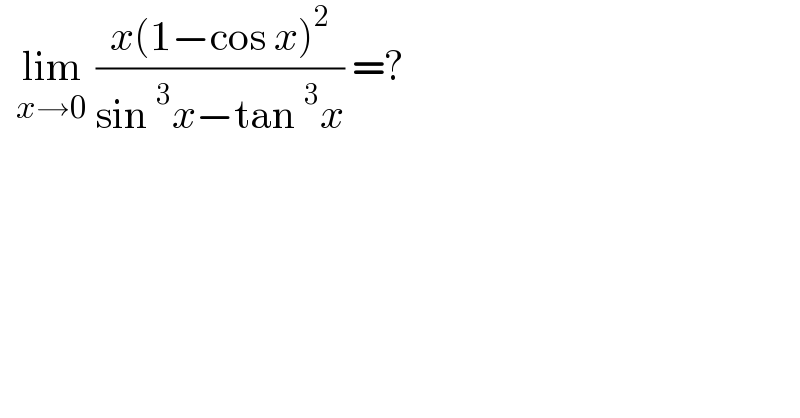 | ||
Answered by iloveisrael last updated on 27/May/21 | ||
![lim_(x→0) ((x(2sin^2 ((x/2)))^2 )/(tan^3 x(cos^3 x−1))) = lim_(x→0) ((4sin^4 ((x/2)))/(tan^2 x(−2sin^2 ((x/2)))(cos^2 x+cos x+1))) = (1/3).lim_(x→0) ((−2sin^2 ((x/2)))/(tan^2 x)) = (1/3). [−2((1/4))] = −(1/6).](Q142177.png) | ||
| ||
Answered by liberty last updated on 27/May/21 | ||
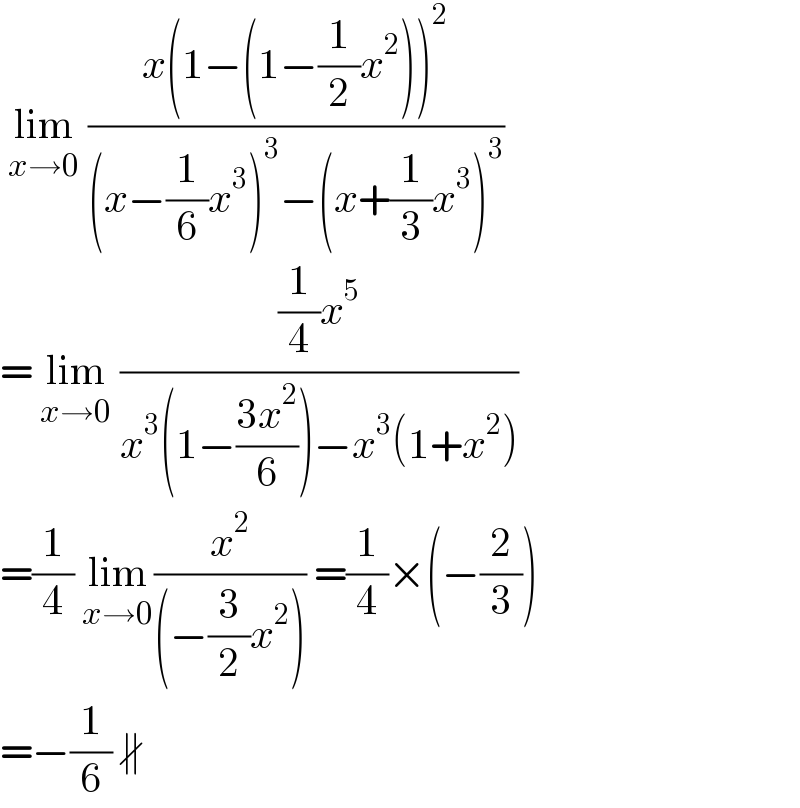 | ||
| ||
Answered by som(math1967) last updated on 27/May/21 | ||
 | ||
| ||