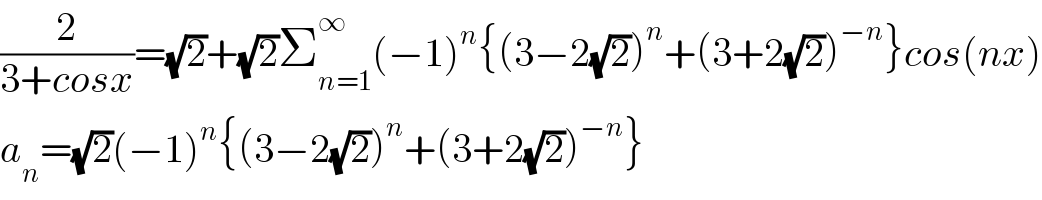developpf(x)=(2/(3+cosx)) at fourier serie


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 142228 by mathmax by abdo last updated on 28/May/21

$developpf (x) = \frac{2}{3 + cosx} at fourier serie$
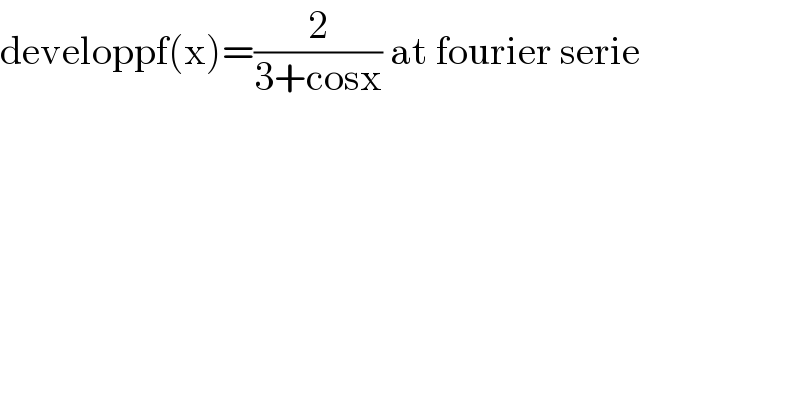
	Answered by mathmax by abdo last updated on 28/May/21
	$another way f is even ⇒f(x)=(a_o /2) +Σ_(n=1) ^∞ a_n cos(nx) a_n =(2/T)∫_([T]) f(x)cos(nx) =(2/(2π))∫_0 ^(2π) (2/(3+cosx))cos(nx)dx =(2/π)∫_0 ^(2π) ((cos(nx))/(3+cosx))dx ⇒(π/2)a_n =∫_0 ^(2π) ((cos(nx))/(3+cosx))dx =_(e^(ix) =z) ∫_(∣z∣=1) (((z^n +z^(−n) )/2)/(3+((z+z^(−1) )/2)))(dz/(iz))=−2i∫_(∣z∣=1) ((z^n +z^(−n) )/((6+z+z^(−1) )z))dz =−2i∫_(∣z∣=1) ((z^n +z^(−n) )/(z^2 +6z +1))dz let ϕ(z)=((z^n +z^(−n) )/(z^2 +6z +1)) poles of ϕ! Δ^′ =8 ⇒z_1 =−3+2(√2) and z_2 =−3−2(√2) ⇒ϕ(z)=((z^n +z^(−n) )/((z−z_1 )(z−z_2 ))) ∣z_1 ∣−1 =3−2(√2)−1 =2−2(√2)<0 ⇒∣z_1 ∣<1 ∣z_2 ∣−1=3+2(√2)−1 =2+2(√2)>0 (out of circle) ⇒ ∫_(∣z∣=1) ϕ(z)dz =2iπ Res(ϕ,z_1 ) =2iπ((z_1 ^n +z_1 ^(−n) )/(z_1 −z_2 )) =((2iπ)/(4(√2))){ (−3+2(√2))^n +(−3+2(√2))^(−n) } =((iπ)/(2(√2))){ (−3+2(√2))^n +(−3+2(√2))^(−n) } ⇒ (π/2)a_n =−2i×((iπ)/(2(√2))){(−3+2(√2))^n +(−3+2(√2))^(−n) } =(π/( (√2))){(−3+2(√2))^n [+(−3+2(√2))^n } ⇒a_n =(√2)(−1)^n { (3−2(√2))^n +(3−2(√2))^(−n) } a_o =2(√2)=(2/π)∫_0 ^(2π) (dx/(3+cosx)) ⇒ (2/(3+cosx))=(√2)+(√2)Σ_(n=1) ^∞ (−1)^n {(3−2(√2))^n +(3−2(√2))^(−n) }cos(nx)$
	$another way f is even \Rightarrow f (x) = \frac{a_{o}}{2} + \sum_{n = 1}^{\infty} a_{n} \cos (nx)$ $a_{n} = \frac{2}{T} \int_{[T]} f (x) \cos (nx) = \frac{2}{2 π} \int_{0}^{2 π} \frac{2}{3 + cosx} \cos (nx) dx$ $= \frac{2}{π} \int_{0}^{2 π} \frac{\cos (nx)}{3 + cosx} dx \Rightarrow \frac{π}{2} a_{n} = \int_{0}^{2 π} \frac{\cos (nx)}{3 + cosx} dx$ $=_{e^{ix} = z} \int_{∣ z ∣= 1} \frac{\frac{z^{n} + z^{- n}}{2}}{3 + \frac{z + z^{- 1}}{2}} \frac{dz}{iz} = - 2 i \int_{∣ z ∣= 1} \frac{z^{n} + z^{- n}}{(6 + z + z^{- 1}) z} dz$ $= - 2 i \int_{∣ z ∣= 1} \frac{z^{n} + z^{- n}}{z^{2} + 6 z + 1} dz let φ (z) = \frac{z^{n} + z^{- n}}{z^{2} + 6 z + 1} poles of φ!$ $Δ^{^{'}} = 8 \Rightarrow z_{1} = - 3 + 2 \sqrt{2} and z_{2} = - 3 - 2 \sqrt{2} \Rightarrow φ (z) = \frac{z^{n} + z^{- n}}{(z - z_{1}) (z - z_{2})}$ $∣ z_{1} ∣ - 1 = 3 - 2 \sqrt{2} - 1 = 2 - 2 \sqrt{2} < 0 \Rightarrow∣ z_{1} ∣< 1$ $∣ z_{2} ∣ - 1 = 3 + 2 \sqrt{2} - 1 = 2 + 2 \sqrt{2} > 0 (out of circle) \Rightarrow$ $\int_{∣ z ∣= 1} φ (z) dz = 2 i π Res (φ, z_{1}) = 2 i π \frac{z_{1}^{n} + z_{1}^{- n}}{z_{1} - z_{2}}$ $= \frac{2 i π}{4 \sqrt{2}} {{(- 3 + 2 \sqrt{2})}^{n} + {(- 3 + 2 \sqrt{2})}^{- n}}$ $= \frac{i π}{2 \sqrt{2}} {{(- 3 + 2 \sqrt{2})}^{n} + {(- 3 + 2 \sqrt{2})}^{- n}} \Rightarrow$ $\frac{π}{2} a_{n} = - 2 i \times \frac{i π}{2 \sqrt{2}} {{(- 3 + 2 \sqrt{2})}^{n} + {(- 3 + 2 \sqrt{2})}^{- n}}$ $= \frac{π}{\sqrt{2}} {{(- 3 + 2 \sqrt{2})}^{n} [+ {(- 3 + 2 \sqrt{2})}^{n}}$ $\Rightarrow a_{n} = \sqrt{2} {(- 1)}^{n} {{(3 - 2 \sqrt{2})}^{n} + {(3 - 2 \sqrt{2})}^{- n}}$ $a_{o} = 2 \sqrt{2} = \frac{2}{π} \int_{0}^{2 π} \frac{dx}{3 + cosx} \Rightarrow$ $\frac{2}{3 + cosx} = \sqrt{2} + \sqrt{2} \sum_{n = 1}^{\infty} {(- 1)}^{n} {{(3 - 2 \sqrt{2})}^{n} + {(3 - 2 \sqrt{2})}^{- n}} \cos (nx)$
	Commented by Mathspace last updated on 28/May/21
	$(2/(3+cosx))=(√2)+(√2)Σ_(n=1) ^∞ (−1)^n {(3−2(√2))^n +(3+2(√2))^(−n) }cos(nx) a_n =(√2)(−1)^n {(3−2(√2))^n +(3+2(√2))^(−n) }$
	$\frac{2}{3 + c o s x} = \sqrt{2} + \sqrt{2} \sum_{n = 1}^{\infty} {(- 1)}^{n} {{(3 - 2 \sqrt{2})}^{n} + {(3 + 2 \sqrt{2})}^{- n}} c o s (n x)$ $a_{n} = \sqrt{2} {(- 1)}^{n} {{(3 - 2 \sqrt{2})}^{n} + {(3 + 2 \sqrt{2})}^{- n}}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum