Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 142236 by mathocean1 last updated on 28/May/21

f is an endomorphism of V such that f○f=−Id_V . 1. Show that f is an isomorphism of V and express f^(−1) in function of f. 2. show that 0^→ is the one invariant vector by f. 3. Given u^→ ≠0^→ and u^→ ∈ V. a. Show that (u^→ ; f(u^→ )) is a base of V. b. Write the matrix of f in base (u^→ ; f(u^→ )).

$$\mathrm{f}\:\mathrm{is}\:\mathrm{an}\:\mathrm{endomorphism}\:\mathrm{of}\:\mathrm{V}\:\mathrm{such} \\ $$$$\mathrm{that}\:\mathrm{f}\circ\mathrm{f}=−\mathrm{Id}_{\mathrm{V}} \:. \\ $$$$\mathrm{1}.\:\mathrm{Show}\:\mathrm{that}\:\mathrm{f}\:\mathrm{is}\:\mathrm{an}\:\mathrm{isomorphism}\:\mathrm{of} \\ $$$$\mathrm{V}\:\mathrm{and}\:\mathrm{express}\:\mathrm{f}^{−\mathrm{1}} \:\mathrm{in}\:\mathrm{function}\:\mathrm{of}\:\mathrm{f}. \\ $$$$\mathrm{2}.\:\mathrm{show}\:\mathrm{that}\:\overset{\rightarrow} {\mathrm{0}}\:\mathrm{is}\:\mathrm{the}\:\mathrm{one}\:\mathrm{invariant} \\ $$$$\mathrm{vector}\:\mathrm{by}\:\mathrm{f}. \\ $$$$\mathrm{3}.\:\mathrm{Given}\:\overset{\rightarrow} {\mathrm{u}}\neq\overset{\rightarrow} {\mathrm{0}}\:\mathrm{and}\:\overset{\rightarrow} {\mathrm{u}}\:\in\:\mathrm{V}. \\ $$$$\mathrm{a}.\:\mathrm{Show}\:\mathrm{that}\:\left(\overset{\rightarrow} {\mathrm{u}};\:\mathrm{f}\left(\overset{\rightarrow} {\mathrm{u}}\right)\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{base}\:\mathrm{of}\:\mathrm{V}. \\ $$$$\mathrm{b}.\:\mathrm{Write}\:\mathrm{the}\:\mathrm{matrix}\:\mathrm{of}\:\mathrm{f}\:\mathrm{in}\:\mathrm{base} \\ $$$$\left(\overset{\rightarrow} {\mathrm{u}};\:\mathrm{f}\left(\overset{\rightarrow} {\mathrm{u}}\right)\right). \\ $$

Answered by mindispower last updated on 28/May/21

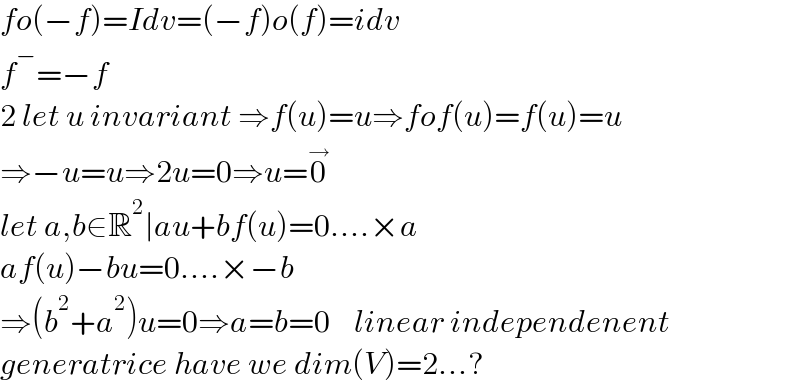
fo(−f)=Idv=(−f)o(f)=idv f^− =−f 2 let u invariant ⇒f(u)=u⇒fof(u)=f(u)=u ⇒−u=u⇒2u=0⇒u=0^→ let a,b∈R^2 ∣au+bf(u)=0....×a af(u)−bu=0....×−b ⇒(b^2 +a^2 )u=0⇒a=b=0 linear independenent generatrice have we dim(V)=2...?

$${fo}\left(−{f}\right)={Idv}=\left(−{f}\right){o}\left({f}\right)={idv} \\ $$$${f}^{−} =−{f} \\ $$$$\mathrm{2}\:{let}\:{u}\:{invariant}\:\Rightarrow{f}\left({u}\right)={u}\Rightarrow{fof}\left({u}\right)={f}\left({u}\right)={u} \\ $$$$\Rightarrow−{u}={u}\Rightarrow\mathrm{2}{u}=\mathrm{0}\Rightarrow{u}=\overset{\rightarrow} {\mathrm{0}} \\ $$$${let}\:{a},{b}\in\mathbb{R}^{\mathrm{2}} \mid{au}+{bf}\left({u}\right)=\mathrm{0}....×{a} \\ $$$${af}\left({u}\right)−{bu}=\mathrm{0}....×−{b} \\ $$$$\Rightarrow\left({b}^{\mathrm{2}} +{a}^{\mathrm{2}} \right){u}=\mathrm{0}\Rightarrow{a}={b}=\mathrm{0}\:\:\:\:{linear}\:{independenent} \\ $$$${generatrice}\:{have}\:{we}\:{dim}\left({V}\right)=\mathrm{2}...? \\ $$

Commented by mathocean1 last updated on 28/May/21

thank you sir. yes dim(V)=2. what could be the matrix..

$${thank}\:{you}\:{sir}. \\ $$$${yes}\:{dim}\left({V}\right)=\mathrm{2}. \\ $$$${what}\:{could}\:{be}\:{the}\:{matrix}.. \\ $$

Commented by mindispower last updated on 28/May/21

(((0 −1)),((1 0)) )

$$\begin{pmatrix}{\mathrm{0}\:−\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\mathrm{0}}\end{pmatrix}\:\:\: \\ $$

Commented by mathocean1 last updated on 29/May/21

Thanks

$${Thanks} \\ $$

Commented by mindispower last updated on 29/May/21

pleasur

$${pleasur} \\ $$

Answered by mindispower last updated on 28/May/21

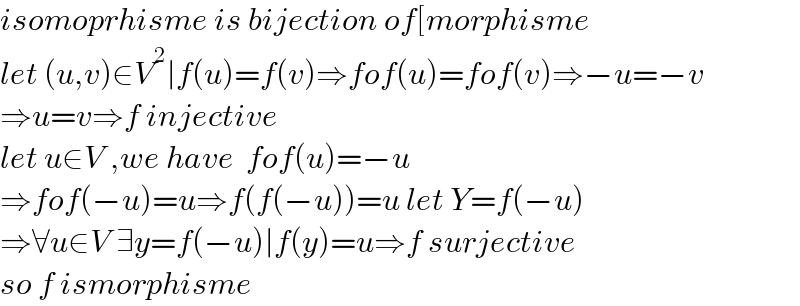
isomoprhisme is bijection of[morphisme let (u,v)∈V^2 ∣f(u)=f(v)⇒fof(u)=fof(v)⇒−u=−v ⇒u=v⇒f injective let u∈V ,we have fof(u)=−u ⇒fof(−u)=u⇒f(f(−u))=u let Y=f(−u) ⇒∀u∈V ∃y=f(−u)∣f(y)=u⇒f surjective so f ismorphisme

$${isomoprhisme}\:{is}\:{bijection}\:{of}\left[{morphisme}\right. \\ $$$${let}\:\left({u},{v}\right)\in{V}^{\mathrm{2}} \mid{f}\left({u}\right)={f}\left({v}\right)\Rightarrow{fof}\left({u}\right)={fof}\left({v}\right)\Rightarrow−{u}=−{v} \\ $$$$\Rightarrow{u}={v}\Rightarrow{f}\:{injective} \\ $$$${let}\:{u}\in{V}\:,{we}\:{have}\:\:{fof}\left({u}\right)=−{u} \\ $$$$\Rightarrow{fof}\left(−{u}\right)={u}\Rightarrow{f}\left({f}\left(−{u}\right)\right)={u}\:{let}\:{Y}={f}\left(−{u}\right) \\ $$$$\Rightarrow\forall{u}\in{V}\:\exists{y}={f}\left(−{u}\right)\mid{f}\left({y}\right)={u}\Rightarrow{f}\:{surjective} \\ $$$${so}\:{f}\:{ismorphisme} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com