
Question and Answers Forum
Question Number 142285 by qaz last updated on 29/May/21
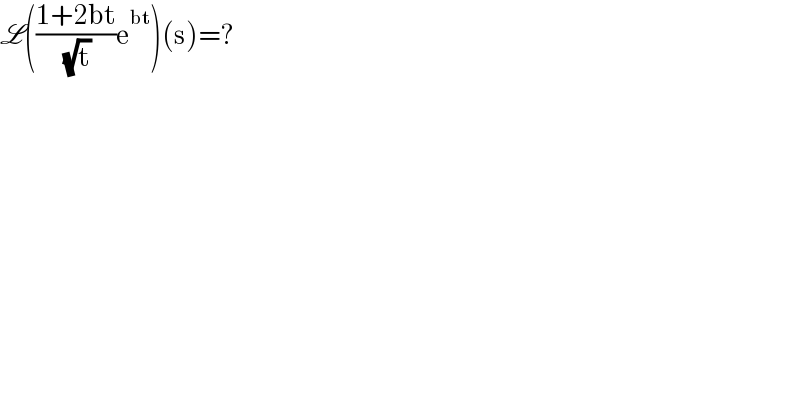
Answered by Dwaipayan Shikari last updated on 29/May/21
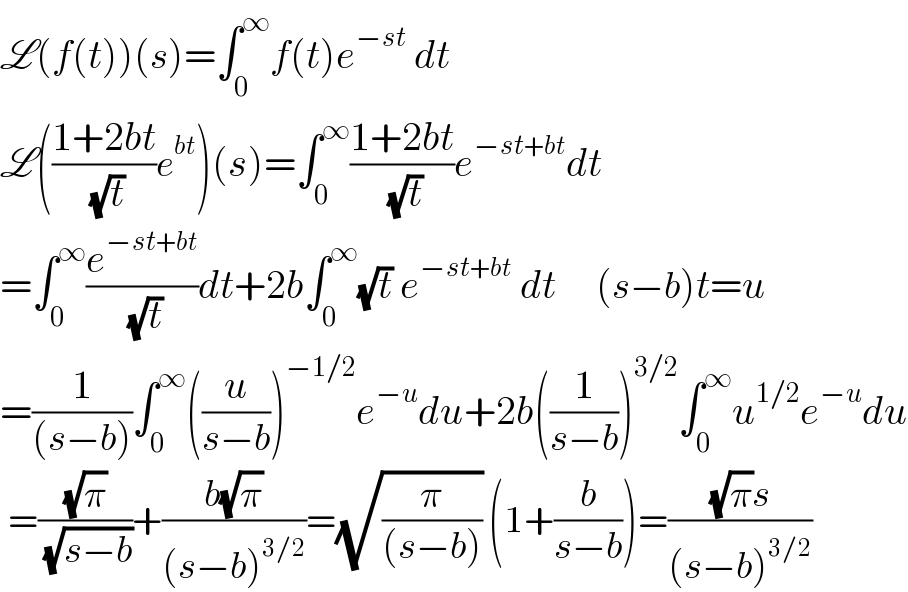
Answered by mathmax by abdo last updated on 29/May/21
![L(((1+2bx)/( (√x)))e^(bx) )(s)=∫_0 ^∞ ((1+2bx)/( (√x)))e^(bx) e^(−sx) dx =∫_0 ^∞ ((1+2bx)/( (√x)))e^(−(s−b)x) dx =_((√x)=t) ∫_0 ^∞ ((1+2bt^2 )/t)e^(−(s−b)t^2 ) (2t)dt =2∫_0 ^∞ (1+2bt^2 )e^(−(s−b)t^2 ) dt =2∫_0 ^∞ e^(−(s−b)t^2 ) dt+4b∫_0 ^∞ t^2 e^(−(s−b)t^2 ) dt we have ∫_0 ^∞ e^(−(s−b)t^2 ) dt =_((√(s−b))t=z) ∫_0 ^∞ e^(−z^2 ) (dz/( (√(s−b))))=(1/( (√(s−b)))).((√π)/2) =((√π)/(2(√(s−b)))) ∫_0 ^∞ t^2 e^(−(s−b)t^2 ) dt =_((√(s−b))t=z) ∫_0 ^∞ (z^2 /(s−b))e^(−z^2 ) (dz/( (√(s−b))))=(1/((s−b)^(3/2) ))∫_0 ^∞ z^2 e^(−z^2 ) dz by parts ∫_0 ^∞ z^2 e^(−z^2 ) dz =−(1/2)∫_0 ^∞ z(−2z)e^(−z^2 ) dz =−(1/2){[ze^(−z^2 ) ]_0 ^∞ −∫_0 ^∞ e^(−z^2 ) dz} =(1/2).((√π)/2)=((√π)/4) ⇒ L(((1+2bx)/( (√x)))e^(bx) ) =((√π)/( (√(s−b))))+4b.(1/((s−b)^(3/2) )).((√π)/4) =((√π)/( (√(s−b))))+((b(√π))/((s−b)^(3/2) ))](Q142293.png)
| ||
Question and Answers Forum | ||
Question Number 142285 by qaz last updated on 29/May/21 | ||
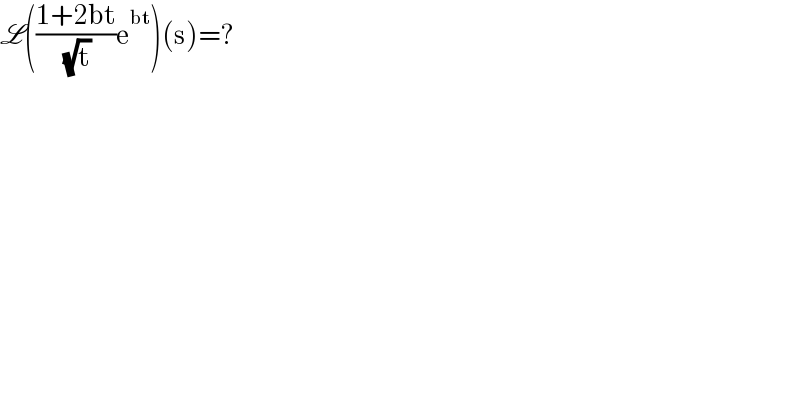 | ||
Answered by Dwaipayan Shikari last updated on 29/May/21 | ||
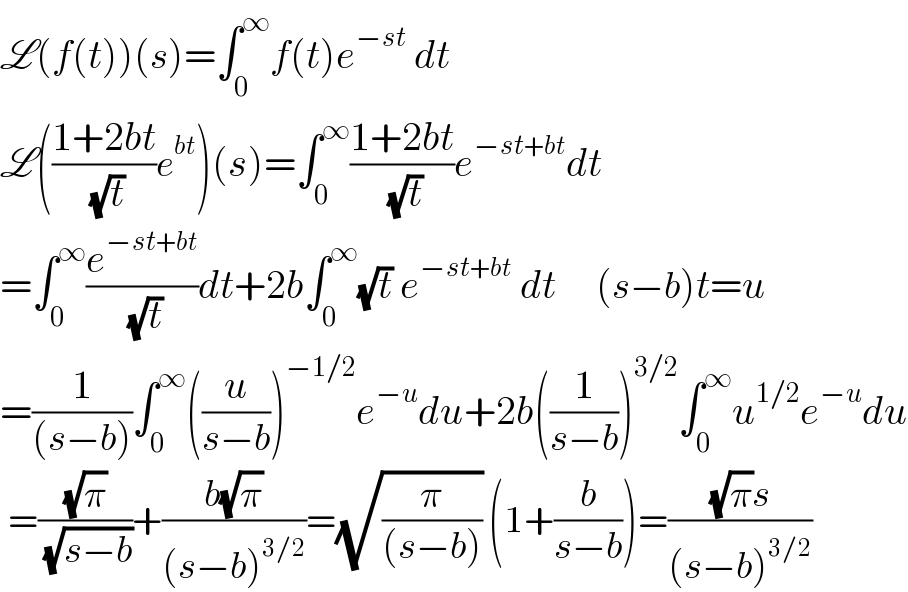 | ||
| ||
Answered by mathmax by abdo last updated on 29/May/21 | ||
![L(((1+2bx)/( (√x)))e^(bx) )(s)=∫_0 ^∞ ((1+2bx)/( (√x)))e^(bx) e^(−sx) dx =∫_0 ^∞ ((1+2bx)/( (√x)))e^(−(s−b)x) dx =_((√x)=t) ∫_0 ^∞ ((1+2bt^2 )/t)e^(−(s−b)t^2 ) (2t)dt =2∫_0 ^∞ (1+2bt^2 )e^(−(s−b)t^2 ) dt =2∫_0 ^∞ e^(−(s−b)t^2 ) dt+4b∫_0 ^∞ t^2 e^(−(s−b)t^2 ) dt we have ∫_0 ^∞ e^(−(s−b)t^2 ) dt =_((√(s−b))t=z) ∫_0 ^∞ e^(−z^2 ) (dz/( (√(s−b))))=(1/( (√(s−b)))).((√π)/2) =((√π)/(2(√(s−b)))) ∫_0 ^∞ t^2 e^(−(s−b)t^2 ) dt =_((√(s−b))t=z) ∫_0 ^∞ (z^2 /(s−b))e^(−z^2 ) (dz/( (√(s−b))))=(1/((s−b)^(3/2) ))∫_0 ^∞ z^2 e^(−z^2 ) dz by parts ∫_0 ^∞ z^2 e^(−z^2 ) dz =−(1/2)∫_0 ^∞ z(−2z)e^(−z^2 ) dz =−(1/2){[ze^(−z^2 ) ]_0 ^∞ −∫_0 ^∞ e^(−z^2 ) dz} =(1/2).((√π)/2)=((√π)/4) ⇒ L(((1+2bx)/( (√x)))e^(bx) ) =((√π)/( (√(s−b))))+4b.(1/((s−b)^(3/2) )).((√π)/4) =((√π)/( (√(s−b))))+((b(√π))/((s−b)^(3/2) ))](Q142293.png) | ||
| ||