
Question and Answers Forum
Question Number 14243 by tawa tawa last updated on 30/May/17
![∫ [x (lnx)^2 ] dx](Q14243.png)
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17
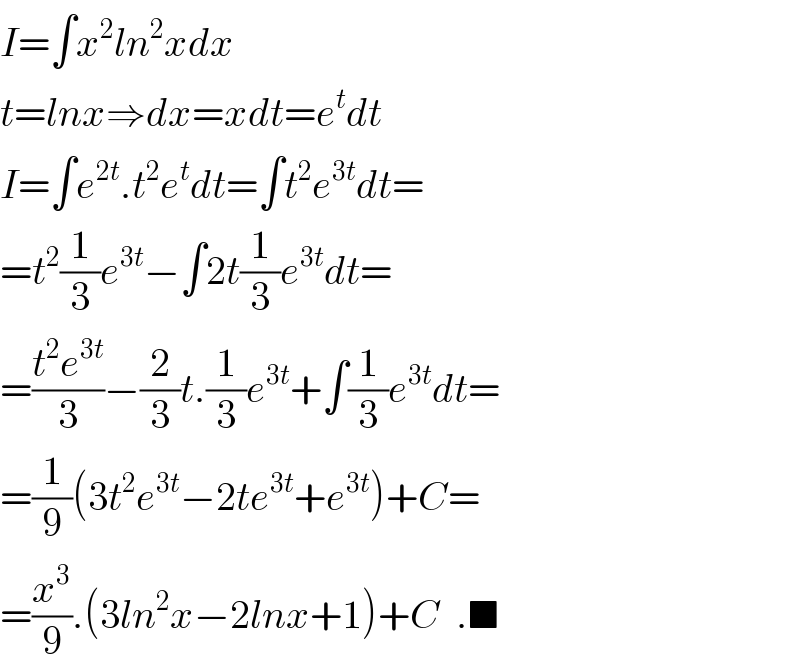
Commented by tawa tawa last updated on 30/May/17
![sir, i think the square is affecting only lnx as in [x (lnx)^2 ] dx](Q14248.png)
Commented by tawa tawa last updated on 30/May/17
![Not [x ln(x)]^2 it is [x (lnx)^2 ] dx](Q14249.png)
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17
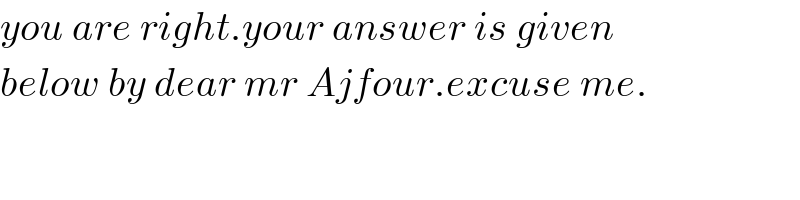
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/May/17

Commented by chux last updated on 30/May/17
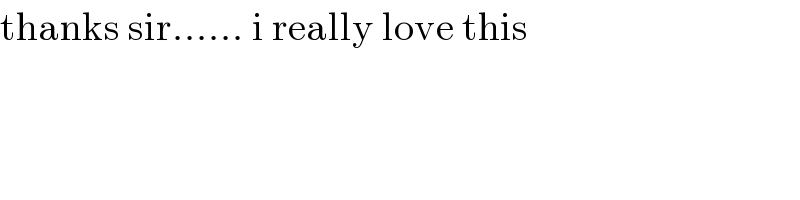
Commented by tawa tawa last updated on 30/May/17

Answered by ajfour last updated on 30/May/17
![let ln x=t ⇒ x=e^t and dx=e^t dt I=∫[x(ln x)^2 ]dx = ∫e^t (t^2 )(e^t dt)=∫t^2 e^(2t) dt = (t^2 /2)e^(2t) −∫((e^(2t) /2)(2t)dt+C_1 =(t^2 /2)e^(2t) −∫te^(2t) dt+C_1 =(t^2 /2)e^(2t) −[((te^(2t) )/2)−∫ (e^(2t) /2)dt]+C_1 I=(t^2 /2)e^(2t) −((te^(2t) )/2)+(e^(2t) /4)+C_1 +C_2 I=(e^(2t) /4)(2t^2 −2t+1)+C I=(x^2 /4)[2(ln x)^2 −2(ln x)+1]+C .](Q14251.png)
Commented by tawa tawa last updated on 30/May/17

