
Question and Answers Forum
Question Number 142457 by ajfour last updated on 01/Jun/21
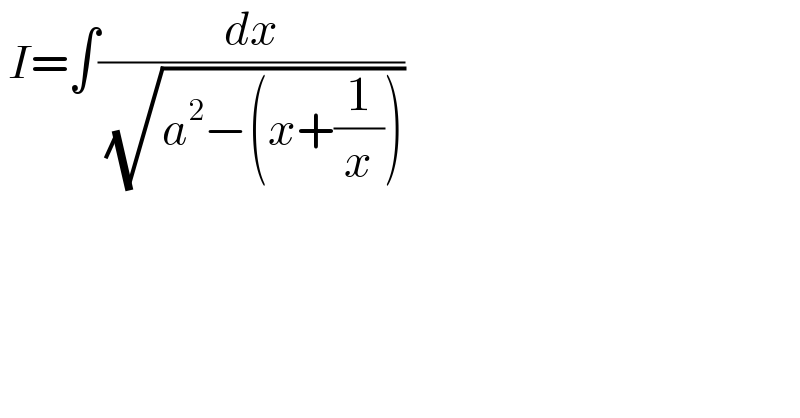
Answered by MJS_new last updated on 01/Jun/21
![I′m afraid you′re ending on elliptic functions again. my try: ∫(dx/( (√(a^2 −(x+(1/x))))))= [t=x+(1/x) → dx=((t+(√(t^2 −4)))/( (√(t^2 −4))))] =(1/2)∫((t+(√(t^2 −4)))/( (√(t^2 −4))(√(a^2 −t))))dt= =(1/2)∫(dt/( (√(a^2 −t))))+(1/2)∫(t/( (√(t^2 −4))(√(a^2 −t))))dt= =−(√(a^2 −t))+(1/2)∫(t/( (√(t^2 −4))(√(a^2 −t))))dt (1/2)∫(t/( (√(t^2 −4))(√(a^2 −t))))dt= [u=((√(t^2 −4))/( (√(a^2 −t)))) → dt=−((2(√(t^2 −4))(√((a^2 −t)^3 )))/(t^2 −2a^2 t+4))] =(1/2)∫du−(1/2)∫(u^2 /( (√(u^4 +4a^2 u^2 +16))))du= =(u/2)−(1/2)∫(u^2 /( (√(u^4 +4a^2 u^2 +16))))du and we cannot solve the remaining integral using elementary calculus](Q142472.png)
Commented by ajfour last updated on 01/Jun/21

| ||
Question and Answers Forum | ||
Question Number 142457 by ajfour last updated on 01/Jun/21 | ||
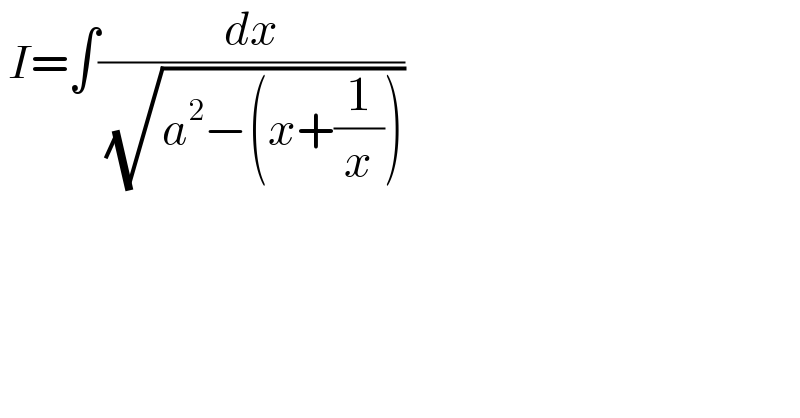 | ||
Answered by MJS_new last updated on 01/Jun/21 | ||
![I′m afraid you′re ending on elliptic functions again. my try: ∫(dx/( (√(a^2 −(x+(1/x))))))= [t=x+(1/x) → dx=((t+(√(t^2 −4)))/( (√(t^2 −4))))] =(1/2)∫((t+(√(t^2 −4)))/( (√(t^2 −4))(√(a^2 −t))))dt= =(1/2)∫(dt/( (√(a^2 −t))))+(1/2)∫(t/( (√(t^2 −4))(√(a^2 −t))))dt= =−(√(a^2 −t))+(1/2)∫(t/( (√(t^2 −4))(√(a^2 −t))))dt (1/2)∫(t/( (√(t^2 −4))(√(a^2 −t))))dt= [u=((√(t^2 −4))/( (√(a^2 −t)))) → dt=−((2(√(t^2 −4))(√((a^2 −t)^3 )))/(t^2 −2a^2 t+4))] =(1/2)∫du−(1/2)∫(u^2 /( (√(u^4 +4a^2 u^2 +16))))du= =(u/2)−(1/2)∫(u^2 /( (√(u^4 +4a^2 u^2 +16))))du and we cannot solve the remaining integral using elementary calculus](Q142472.png) | ||
| ||
Commented by ajfour last updated on 01/Jun/21 | ||
 | ||