
Question and Answers Forum
Question Number 142595 by qaz last updated on 02/Jun/21
![Prove :: sec^2 x=4Σ_(n=0) ^∞ {(1/([(2n+1)π−2x]^2 ))+(1/([(2n+1)π+2x]^2 ))}](Q142595.png)
Answered by Dwaipayan Shikari last updated on 02/Jun/21
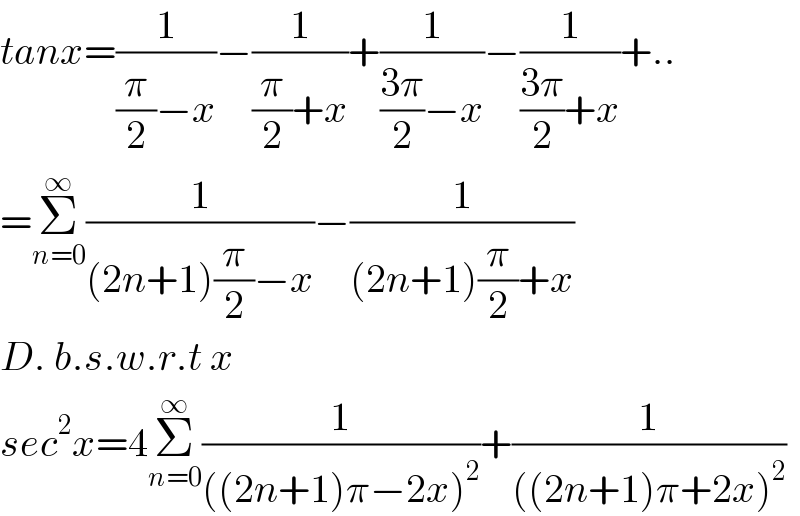
| ||
Question and Answers Forum | ||
Question Number 142595 by qaz last updated on 02/Jun/21 | ||
![Prove :: sec^2 x=4Σ_(n=0) ^∞ {(1/([(2n+1)π−2x]^2 ))+(1/([(2n+1)π+2x]^2 ))}](Q142595.png) | ||
Answered by Dwaipayan Shikari last updated on 02/Jun/21 | ||
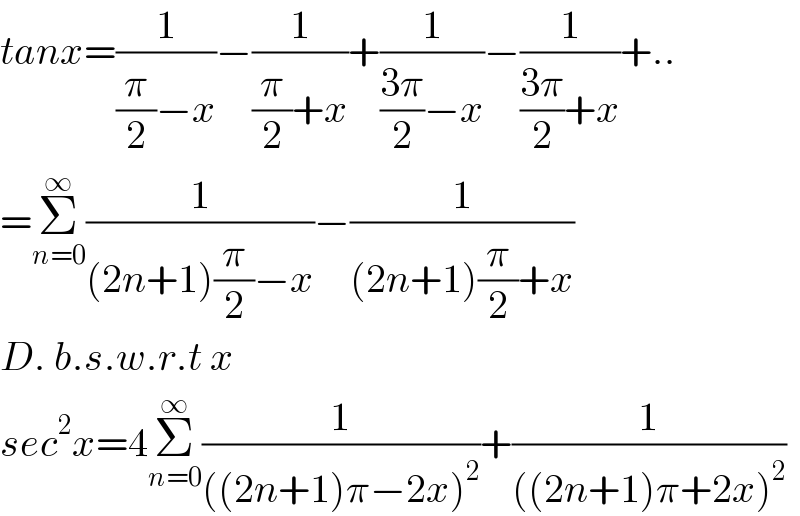 | ||
| ||