
Question and Answers Forum
Question Number 142629 by qaz last updated on 03/Jun/21
![Σ_(n=1) ^∞ (−1)^n ∙((2n−1)/((2n)!))∙((π/2))^(2n) =Σ_(n=1) ^∞ ((2n−1)/((2n)!))∙(−((π/2))^2 )^n =(2xD−1)∣_(x=π/2) Σ_(n=1) ^∞ (((−x^2 )^n )/((2n)!)) =(2xD−1)∣_(x=π/2) [Σ_(n=0) ^∞ (((−x^2 )^n )/((2n)!))−1] =(2xD−1)∣_(x=π/2) (cos x−1) =(−2xsin x−cos x+1)∣_(x=π/2) =1−π where is wrong?](Q142629.png)
Answered by Dwaipayan Shikari last updated on 03/Jun/21
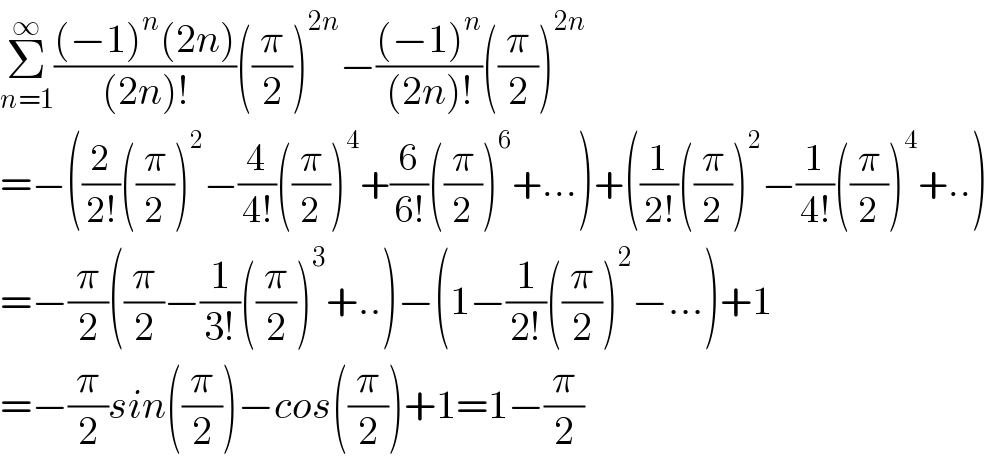
Commented by qaz last updated on 03/Jun/21
![i have another solution. Σ_(n=1) ^∞ (((−1)^n (2n−1))/((2n)!))x^(2n) ∣_(x=(π/2)) =Σ_(n=0) ^∞ (((−1)^(n+1) (2n+1))/((2n+2)!))x^(2n+2) ∣_(x=(π/2)) =−x^2 Σ_(n=0) ^∞ (((−1)^n )/((2n+2)(2n)!))x^(2n) =−x^2 ∫_0 ^1 yΣ_(n=0) ^∞ (((−1)^n )/((2n)!))∙(xy)^(2n) dy =−x^2 ∫_0 ^1 ycos (xy)dy =−x^2 {[(1/x)ysin (xy)+(1/x^2 )cos (xy)]_0 ^1 }_(x=(π/2)) =−x^2 {(1/x)sin x+(1/x^2 )(cos x−1)}_(x=(π/2)) =1−(π/2) −−−−−−−−−−−−−−−−−−− but Σ_(n=1) ^∞ (2n−1)(((−1)^n )/((2n)!))x^(2n) =(xD−1)(cos x−1), i still dont understand,why not LFT=(2xD−1)(cos x−1)???](Q142645.png)
| ||
Question and Answers Forum | ||
Question Number 142629 by qaz last updated on 03/Jun/21 | ||
![Σ_(n=1) ^∞ (−1)^n ∙((2n−1)/((2n)!))∙((π/2))^(2n) =Σ_(n=1) ^∞ ((2n−1)/((2n)!))∙(−((π/2))^2 )^n =(2xD−1)∣_(x=π/2) Σ_(n=1) ^∞ (((−x^2 )^n )/((2n)!)) =(2xD−1)∣_(x=π/2) [Σ_(n=0) ^∞ (((−x^2 )^n )/((2n)!))−1] =(2xD−1)∣_(x=π/2) (cos x−1) =(−2xsin x−cos x+1)∣_(x=π/2) =1−π where is wrong?](Q142629.png) | ||
Answered by Dwaipayan Shikari last updated on 03/Jun/21 | ||
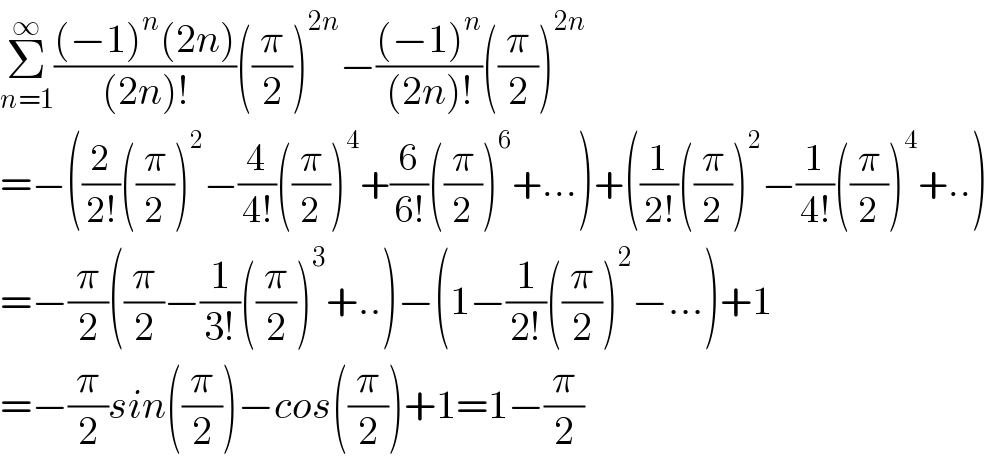 | ||
| ||
Commented by qaz last updated on 03/Jun/21 | ||
![i have another solution. Σ_(n=1) ^∞ (((−1)^n (2n−1))/((2n)!))x^(2n) ∣_(x=(π/2)) =Σ_(n=0) ^∞ (((−1)^(n+1) (2n+1))/((2n+2)!))x^(2n+2) ∣_(x=(π/2)) =−x^2 Σ_(n=0) ^∞ (((−1)^n )/((2n+2)(2n)!))x^(2n) =−x^2 ∫_0 ^1 yΣ_(n=0) ^∞ (((−1)^n )/((2n)!))∙(xy)^(2n) dy =−x^2 ∫_0 ^1 ycos (xy)dy =−x^2 {[(1/x)ysin (xy)+(1/x^2 )cos (xy)]_0 ^1 }_(x=(π/2)) =−x^2 {(1/x)sin x+(1/x^2 )(cos x−1)}_(x=(π/2)) =1−(π/2) −−−−−−−−−−−−−−−−−−− but Σ_(n=1) ^∞ (2n−1)(((−1)^n )/((2n)!))x^(2n) =(xD−1)(cos x−1), i still dont understand,why not LFT=(2xD−1)(cos x−1)???](Q142645.png) | ||