Question Number 142655 by mnjuly1970 last updated on 03/Jun/21
$$\:\:{evaluate}..... \\ $$$$\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{{n}.{cos}\left({n}\pi\right)}{\Gamma\:\left(\mathrm{2}{n}+\mathrm{2}\right)}\right)=?\:..... \\ $$$$\:\:\:....... \\ $$
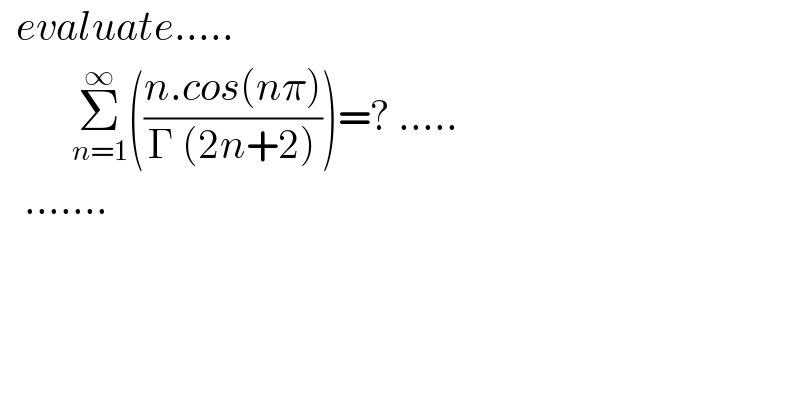
Answered by qaz last updated on 03/Jun/21
![Σ_(n=1) ^∞ ((n∙cos (nπ))/(Γ(2n+2))) =ℜΣ_(n=1) ^∞ ((n∙e^(inπ) )/((2n+1)!)) =Σ_(n=1) ^∞ ((n∙(−1)^n )/((2n+1)!)) =Σ_(n=0) ^∞ ((n∙(−1)^n )/((2n+1)!))x^(2n+1) ∣_(x=1) =(1/2)Σ_(n=0) ^∞ [(((2n+1))/((2n+1)!))(−1)^n x^(2n+1) −(((−1)^n x^(2n+1) )/((2n+1)!))]_(x=1) =(1/2)(xDsin x−sin x)∣_(x=1) =(1/2)(xcos x−sin x)∣_(x=1) =(1/2)(cos 1−sin 1) nice problem .sir](Q142676.png)
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{n}\centerdot\mathrm{cos}\:\left(\mathrm{n}\pi\right)}{\Gamma\left(\mathrm{2n}+\mathrm{2}\right)} \\ $$$$=\Re\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{n}\centerdot\mathrm{e}^{\mathrm{in}\pi} }{\left(\mathrm{2n}+\mathrm{1}\right)!} \\ $$$$=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{n}\centerdot\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!} \\ $$$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{n}\centerdot\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \mid_{\mathrm{x}=\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\left(\mathrm{2n}+\mathrm{1}\right)}{\left(\mathrm{2n}+\mathrm{1}\right)!}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{2n}+\mathrm{1}} −\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\right]_{\mathrm{x}=\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{xDsin}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)\mid_{\mathrm{x}=\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{xcos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)\mid_{\mathrm{x}=\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\mathrm{1}−\mathrm{sin}\:\mathrm{1}\right) \\ $$$$\mathrm{nice}\:\mathrm{problem}\:.\mathrm{sir} \\ $$
Commented by mnjuly1970 last updated on 03/Jun/21
$${thanks}\:{alot}\:{mr}\:{qaz} \\ $$$$\:{very}\:{nice}\:{as}\:{always}... \\ $$
Answered by Dwaipayan Shikari last updated on 03/Jun/21
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}={sin}\left({x}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {x}^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}=\frac{{sin}\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}} \\ $$$${D}.{B}.{S}.{W}.{R}.{T}.{x}\mid_{{x}=\mathrm{1}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)!}=\frac{{d}}{{dx}}\mid_{{x}=\mathrm{1}} \frac{{sin}\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}}=\frac{\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\sqrt{{x}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}{sin}\left(\sqrt{{x}}\right)}{{x}}\mid_{{x}=\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{1}−{sin}\mathrm{1}\right) \\ $$
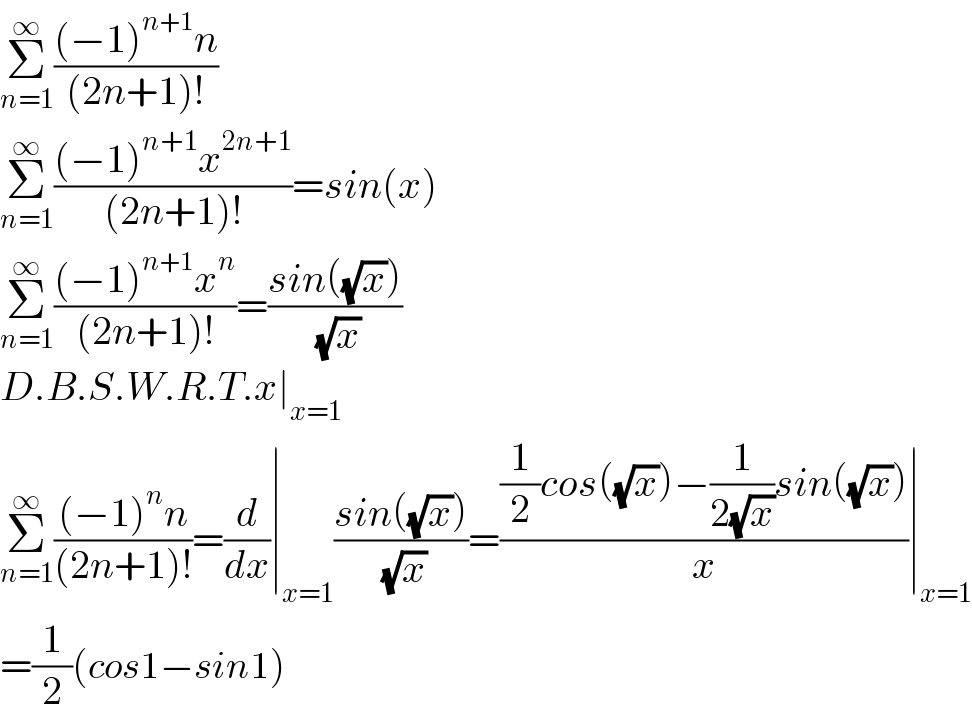
Commented by mnjuly1970 last updated on 03/Jun/21
$${thanks}\:{alot}\:{grateful}... \\ $$$$\:\:{Differentiation}\:{both}\:{sides}\:{with}\:{the}\:\:{respect} \\ $$$$\:{to}\:\:{x}\:\:\: \\ $$
Commented by Dwaipayan Shikari last updated on 03/Jun/21
$${Hahahha} \\ $$