
Question and Answers Forum
Question Number 14267 by Tinkutara last updated on 30/May/17
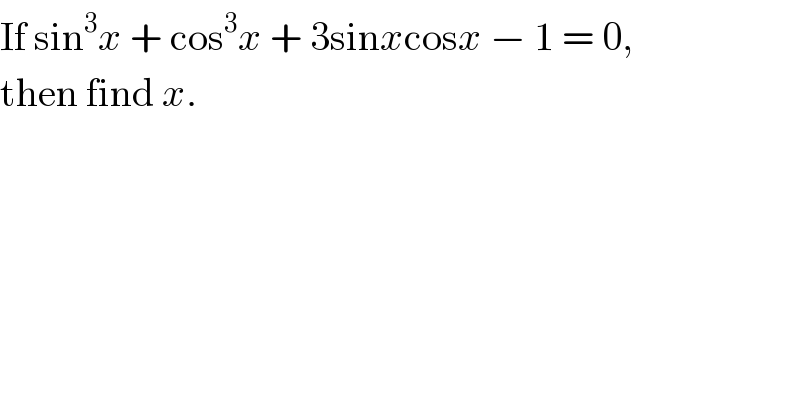
Answered by linkelly0615 last updated on 30/May/17
![set { ((A=sinx+cosx)),((B=sinx−cosx)) :} ⇒ sin^3 x + cos^3 x + 3sinxcosx − 1=0 ⇒A(A^2 −2sinxcosx)−3Asinxcosx+3sinxcosx−1=0 ⇒(1−A)[3sinxcosx−(1+A+A^2 )]=0 ⇒(1−A)[(3/4)(A^2 −B^2 )−(1+A+A^2 )]=0 ⇒(A−1){(1/4)[(A+2)^2 +3B^2 ]}=0 ⇒A=1 or { ((A=(−2))),((B=0)) :} !!BUT!! ∵A=sinx+cosx=(√2)sin (x+(π/4)) ∴∣A∣≤(√2)⇒A won′t be (−2) ⇒so, A=1 {sorry, that′s my fault.} ⇒sinx+cosx=1 [sinx+cosx=(√)2(((sinx)/(√2))+((cosx)/(√2)))=(√2)sin(x+(π/4))] ⇒sin(x+π/4)=1/(√2) ⇒x+π/4=2kπ+π/4 or 2kπ+3π/4 ,k∈Z ⇒x=2kπ or (2k+(1/2))π, k∈Z](Q14281.png)
Commented by Tinkutara last updated on 30/May/17
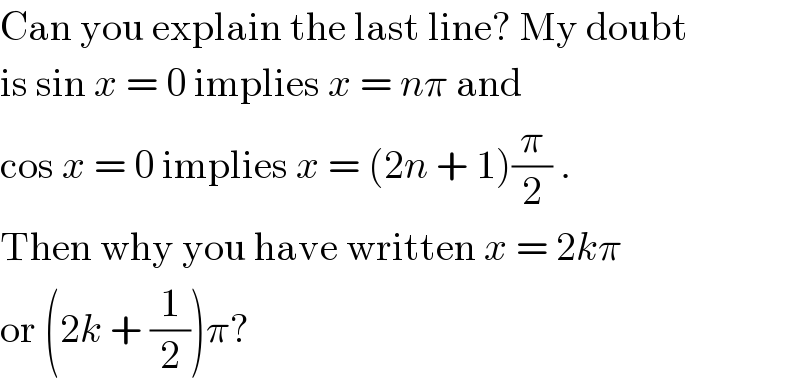
| ||
Question and Answers Forum | ||
Question Number 14267 by Tinkutara last updated on 30/May/17 | ||
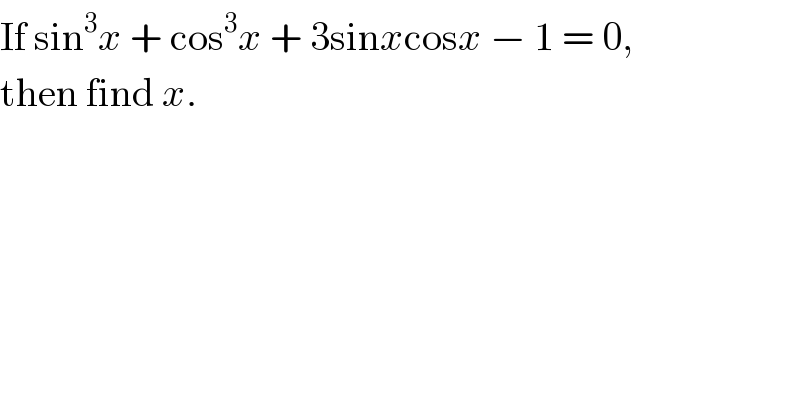 | ||
Answered by linkelly0615 last updated on 30/May/17 | ||
![set { ((A=sinx+cosx)),((B=sinx−cosx)) :} ⇒ sin^3 x + cos^3 x + 3sinxcosx − 1=0 ⇒A(A^2 −2sinxcosx)−3Asinxcosx+3sinxcosx−1=0 ⇒(1−A)[3sinxcosx−(1+A+A^2 )]=0 ⇒(1−A)[(3/4)(A^2 −B^2 )−(1+A+A^2 )]=0 ⇒(A−1){(1/4)[(A+2)^2 +3B^2 ]}=0 ⇒A=1 or { ((A=(−2))),((B=0)) :} !!BUT!! ∵A=sinx+cosx=(√2)sin (x+(π/4)) ∴∣A∣≤(√2)⇒A won′t be (−2) ⇒so, A=1 {sorry, that′s my fault.} ⇒sinx+cosx=1 [sinx+cosx=(√)2(((sinx)/(√2))+((cosx)/(√2)))=(√2)sin(x+(π/4))] ⇒sin(x+π/4)=1/(√2) ⇒x+π/4=2kπ+π/4 or 2kπ+3π/4 ,k∈Z ⇒x=2kπ or (2k+(1/2))π, k∈Z](Q14281.png) | ||
| ||
Commented by Tinkutara last updated on 30/May/17 | ||
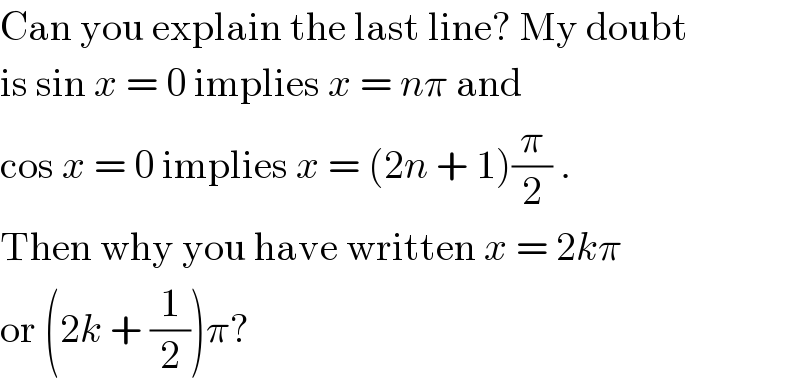 | ||