Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 142689 by rs4089 last updated on 04/Jun/21

Answered by Dwaipayan Shikari last updated on 04/Jun/21

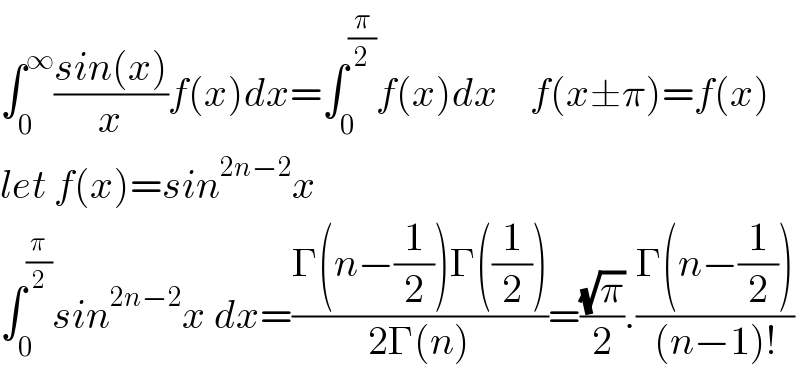
∫_0 ^∞ ((sin(x))/x)f(x)dx=∫_0 ^(π/2) f(x)dx f(x±π)=f(x) let f(x)=sin^(2n−2) x ∫_0 ^(π/2) sin^(2n−2) x dx=((Γ(n−(1/2))Γ((1/2)))/(2Γ(n)))=((√π)/2).((Γ(n−(1/2)))/((n−1)!))

$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right)}{{x}}{f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left({x}\right){dx}\:\:\:\:{f}\left({x}\pm\pi\right)={f}\left({x}\right) \\ $$$${let}\:{f}\left({x}\right)={sin}^{\mathrm{2}{n}−\mathrm{2}} {x}\:\:\:\:\:\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}{n}−\mathrm{2}} {x}\:{dx}=\frac{\Gamma\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left({n}\right)}=\frac{\sqrt{\pi}}{\mathrm{2}}.\frac{\Gamma\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\left({n}−\mathrm{1}\right)!} \\ $$

Commented by mindispower last updated on 04/Jun/21

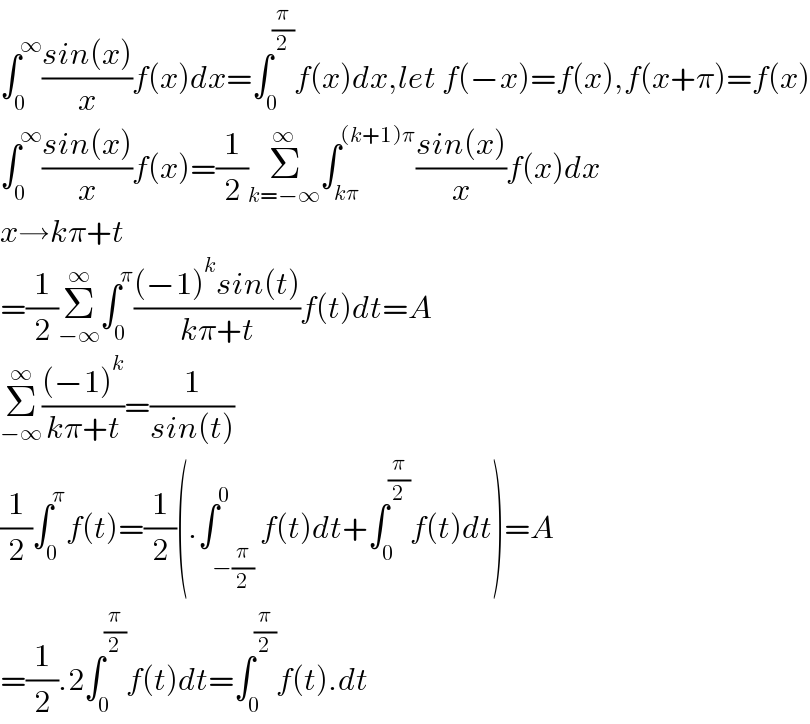
∫_0 ^∞ ((sin(x))/x)f(x)dx=∫_0 ^(π/2) f(x)dx,let f(−x)=f(x),f(x+π)=f(x) ∫_0 ^∞ ((sin(x))/x)f(x)=(1/2)Σ_(k=−∞) ^∞ ∫_(kπ) ^((k+1)π) ((sin(x))/x)f(x)dx x→kπ+t =(1/2)Σ_(−∞) ^∞ ∫_0 ^π (((−1)^k sin(t))/(kπ+t))f(t)dt=A Σ_(−∞) ^∞ (((−1)^k )/(kπ+t))=(1/(sin(t))) (1/2)∫_0 ^π f(t)=(1/2)(.∫_(−(π/2)) ^0 f(t)dt+∫_0 ^(π/2) f(t)dt)=A =(1/2).2∫_0 ^(π/2) f(t)dt=∫_0 ^(π/2) f(t).dt

$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right)}{{x}}{f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left({x}\right){dx},{let}\:{f}\left(−{x}\right)={f}\left({x}\right),{f}\left({x}+\pi\right)={f}\left({x}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right)}{{x}}{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=−\infty} {\overset{\infty} {\sum}}\int_{{k}\pi} ^{\left({k}+\mathrm{1}\right)\pi} \frac{{sin}\left({x}\right)}{{x}}{f}\left({x}\right){dx} \\ $$$${x}\rightarrow{k}\pi+{t} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{−\infty} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\pi} \frac{\left(−\mathrm{1}\right)^{{k}} {sin}\left({t}\right)}{{k}\pi+{t}}{f}\left({t}\right){dt}={A} \\ $$$$\underset{−\infty} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}\pi+{t}}=\frac{\mathrm{1}}{{sin}\left({t}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} {f}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(.\int_{−\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} {f}\left({t}\right){dt}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left({t}\right){dt}\right)={A} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left({t}\right){dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {f}\left({t}\right).{dt} \\ $$

Commented by Dwaipayan Shikari last updated on 04/Jun/21

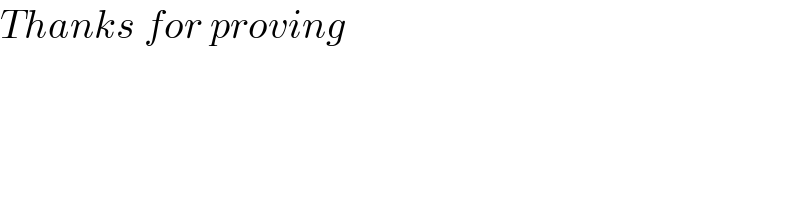
Thanks for proving

$${Thanks}\:{for}\:{proving} \\ $$

Commented by mindispower last updated on 04/Jun/21

pleasur nice answer too

$${pleasur}\:{nice}\:{answer}\:{too} \\ $$

Commented by mathmax by abdo last updated on 06/Jun/21

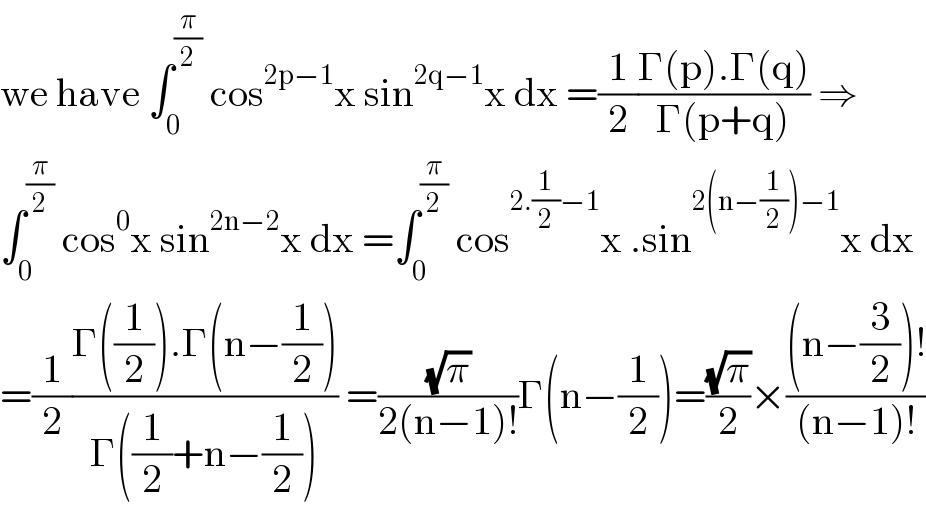
we have ∫_0 ^(π/2) cos^(2p−1) x sin^(2q−1) x dx =(1/2)((Γ(p).Γ(q))/(Γ(p+q))) ⇒ ∫_0 ^(π/2) cos^0 x sin^(2n−2) x dx =∫_0 ^(π/2) cos^(2.(1/2)−1) x .sin^(2(n−(1/2))−1) x dx =(1/2)((Γ((1/2)).Γ(n−(1/2)))/(Γ((1/2)+n−(1/2)))) =((√π)/(2(n−1)!))Γ(n−(1/2))=((√π)/2)×(((n−(3/2))!)/((n−1)!))

$$\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2p}−\mathrm{1}} \mathrm{x}\:\mathrm{sin}^{\mathrm{2q}−\mathrm{1}} \mathrm{x}\:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\frac{\Gamma\left(\mathrm{p}\right).\Gamma\left(\mathrm{q}\right)}{\Gamma\left(\mathrm{p}+\mathrm{q}\right)}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{0}} \mathrm{x}\:\mathrm{sin}^{\mathrm{2n}−\mathrm{2}} \mathrm{x}\:\mathrm{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \mathrm{x}\:.\mathrm{sin}^{\mathrm{2}\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1}} \mathrm{x}\:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right).\Gamma\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=\frac{\sqrt{\pi}}{\mathrm{2}\left(\mathrm{n}−\mathrm{1}\right)!}\Gamma\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}}×\frac{\left(\mathrm{n}−\frac{\mathrm{3}}{\mathrm{2}}\right)!}{\left(\mathrm{n}−\mathrm{1}\right)!} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com