
Question and Answers Forum
Question Number 142939 by Rasheed.Sindhi last updated on 07/Jun/21

Answered by Rasheed.Sindhi last updated on 07/Jun/21

Commented bymr W last updated on 07/Jun/21

Commented bymr W last updated on 07/Jun/21

Commented byRasheed.Sindhi last updated on 08/Jun/21

Commented bymr W last updated on 08/Jun/21
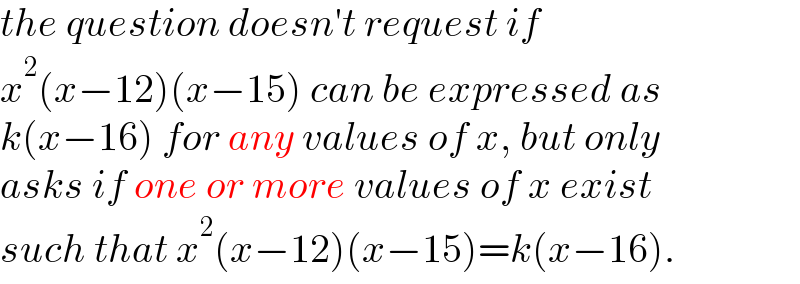
Commented byRasheed.Sindhi last updated on 08/Jun/21
Answered by Rasheed.Sindhi last updated on 07/Jun/21

